PERFORMANCE COMPARISON OF
CONTROLLERS FOR FLEXIBLE LINK
MANIPULATOR

S. Mallikarjunaiah; S. Narayana Reddy

PERFORMANCE COMPARISON OF CONTROLLERS FOR FLEXIBLE LINK MANIPULATOR

S. Mallikarjunaiah¹, S. Narayana Reddy²

Professor, Dept. of EEE, CR Engineering College, Tirupati, Andhra Pradesh, India
Professor, Dept. of ECE, SVU College of Engineering,Tirupati,Andhra Pradesh, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper focuses on the end-point control of a single flexible link which rotates in the horizontal plane. The dynamic model is derived using a Lagrangian assumed modes method based on Euler–Bernoulli beam theory. Initially the system is modelled as a voltage-input model, and different controllers were applied to control the system. The position and trajectory control is performed by PID, LQR and ANFIS control methods for flexible link manipulator. The purpose of this study is to keep the rotate angle of the link at desired position and to eliminate the oscillation angle of end effectors. The position and trajectory control again is performed by advanced controllers like LQR control methods and ANFIS control methods for this system. The results were produced for mode 1 and mode 2 operation. The results of the ANFIS method and LQR method were compared with PID Controller method. The control blocks for flexible link manipulator are performed and compared on MATLAB – SIMULINK with respect various control parameters and integral errors for all controllers.

Keywords

Flexible Link Manipulator, ANFIS controller, LQR Controller, PID Controller, High Frequency modes

I.INTRODUCTION

An important advanced robotic system is the flexible-link robot arm. The desire to improve robot performance has led to the design of lighter flexible links. A light-flexible link robot arm has many advantages compared to conventional rigid link robots such as lower power consumption, higher payload-to-robot weight ratio, lower manufacturing cost, and easier transportation to name a few. Because of the elasticity of the flexible robot arm, the controller algorithms are different from that of the traditional rigid robot arm.

A flexible link robot arm is a distributed parameter system of infinite order, Due to elastic properties of flexible manipulators, the development of a mathematical description and subsequent model-based control of the system is a complicated task. This is made difficult by the presence of a large (infinite) number of modes of vibration in the system. The modes become significant in two ways: firstly, because the oscillations themselves prolong the settling time and secondly, because attempts to actively control some modes result in instability of the other modes. This nonlinear behavior of the structure at high speeds, firstly, degrades end-point accuracy and secondly complicates controller development. Furthermore, the performance of such a control system depends mainly on the parameters during operation. These limitations of conventional model-based control for flexible manipulator systems have stimulated the development of intelligent control mechanisms incorporating adaptive control, neural networks (NNs) and fuzzy logic controllers.

It is known that the flexible system is a highly nonlinear and heavily coupled system, and an accurate mathematical model [1] is difficult to obtain, thus making it difficult to control using conventional techniques. The improved control of a manipulator without a-prior knowledge of its dynamics, such as fuzzy logic or neural network control has attracted much attention in recent years.

A neural network controller [2] invariably includes a neural network that has been trained to model in some way the inverse dynamics of the plant. Hub position and velocity measurements were used to stabilize the system and a neural controller was proposed to drive the flexible arm to track a desired trajectory. This work, however, is restricted only to linear models of the flexible-link manipulator. Another drawback is that the error between the desired and actual outputs is not involved in the network training, or during control. In the specialized learning scheme, errors between the desired and actual outputs of the plant have to be back propagated through the plant to adjust the weights of the network, which is not a simple procedure to implement. The training therefore, may be slow, or may disrupt the operation of the plant.

In order to overcome the above difficulty, Donne &Ozguner [3] proposed a neural controller assuming partial knowledge of the dynamics of the flexible-link. The unknown part of the dynamics is identified by a supervised learning algorithm. The controller is constructed in two stages, an optimal controller and an unsupervised neural network controller using model-based predictive control. The scheme is based on an identification stage that also requires feedback from the states of the system.

Significant efforts have been made to develop neural networks to deal with the problems of identification and control of complex nonlinear systems by exploiting the nonlinear approaching abilities of the neural network .In parallel with these investigations many researchers have similarly been involved in the design of robust controllers for robot manipulators. In [4] a modified version of the fuzzy neural network, is used to identify and control a nonlinear dynamic system. The RFNN is a recurrent multilayered connectionist network for realizing fuzzy inference and can be constructed from a set of fuzzy rules.

In [5], two different schemes are proposed—one with an adaptive state feedback controller and one with an adaptive feed forward controller .In the adaptive feedback formulation, the actual state is used to compute basis functions of a function approximator for parameter update and cancellation of nonlinearities. On the other hand, in the adaptive feed forward formulation, the desired state is used instead of the actual state. In [6], a neural network approach to on-line learning control and real time implementation is developed. The neural network learns control by updating feed forward dynamic based on feedback control input. The manipulator tracking error is reduced by 85% compared to conventional PID control. This approach possesses a high degree of generality and adaptability in various applications and will be a valuable method in learning control for robots working in unconstrained environments.

In [7], simulation and experimental results on the performance of neural network-based controllers for tip position tracking of flexible-link manipulators are presented. The controllers are designed by utilizing the modified output redefinition approach. The modified output re-definition approach requires only a priori knowledge about the linear model of the system and no a priori knowledge about the payload mass.In [8], a neural network controller is employed as a feedback controller to compute the torque needed by the manipulator system. The neural network is made up of two parts. A dynamic recurrent identification network is used to identify the output of the manipulator system, and a dynamic recurrent learning network is employed to automatically learn the weighting factor of the fuzzy logic controller and to compute a suitable value for correct operation of the fuzzy logic controller.In [9], it is shown that the velocity controlled actuator regulation and tracking performance is superior than torque controlled actuator of a flexible one-link robot.

In this paper PID, LQR and ANFIS control of flexible manipulator is taken up. The ANFIS controller is a combination of PID controller and fuzzy neural network controller that is adapted based on the output of PID controller [10].

II.FLEXIBLE LINK MANIPULATOR

The conventional approach to the design of an automatic control system often involves the construction of a mathematical model which best describes the dynamics behaviour of the plant to be controlled, and the application of analytical techniques to this plant model to derive an appropriate control law. Usually, such a mathematical model consist of a set linear or non-linear differential equations, most of them are derived using some form of approximation and simplification. The traditional model-based control techniques break down, when a representative model is difficult to obtain due to uncertainty or sheer complexity. It is known that robot system is highly non-linear and heavily coupled system, and accurate mathematical model is difficult to obtain, thus it making difficult to control using conventional techniques. This paper presents the mathematical modelling of a single link flexible manipulator. The system is modelled by the Lagrange formulation and model expansion method.

A. MATHEMATICAL MODELLING OF FLEXIBLE LINK MANIPULATOR

The manipulator is illustrated in fig. 1, and is modelled as a pinned-free flexible beam with payload at one end. The beam can bend freely in the horizontal plane but is considered stiff with respect to vertical bending and torsion. The model is developed using the Lagrange formulation and model expansion method. The length of the manipulator is assumed to be constant, and deformation due to shear, rotary inertia and the effects of axial forces are neglected. The moment of inertia about the hub O is denoted by jf and p is the linear mass density The arm has length l and the payload mass is given by Me The control torque T is applied at the hub of the manipulator by way of the rotary actuator. The angular displacement of the manipulator, moving in the xOy plane, is denoted by θ The width of the arm is assumed to be much greater than it’s the thickness, thus allowing it to vibrate dominantly in the horizontal direction. The shear deformation and rotary inertia effects are ignored

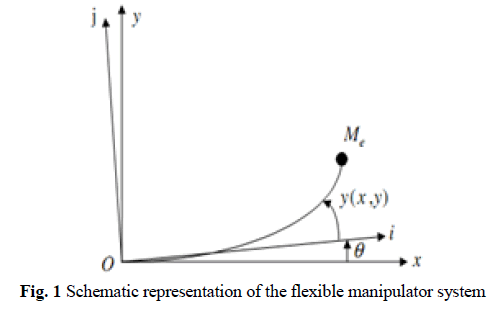For an angular displacement θ and an elastic deflection y(x,t) the total displacement u(x,t) of a point, measured at a distance x from the hub can be described as a function of the above, measured from the direction of Ox.

(x, t) = u(x, t) +θ (t) x (1)

The kinetic energy of the system can be written as

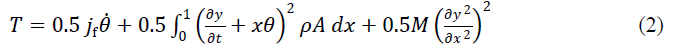In eqn. (2), the first term on the right hand side is due to the hub inertia, the second term is due to the rotation of the manipulator with respect to the origin, and the third term is due to the payload mass.

The potential energy is related to the bending of manipulator. Since the width of the manipulator under consideration is assumed to be significantly larger than its thickness, the effects of the shear displacement can be neglected. In this way, the potential energy of the manipulator can be written as

where

E is the modulus of the elasticity for the beam material, and

I denote the second moment of area of the beam cross-section

The non-conservative work for the input torque T can be written as

W= Tθ (4)

The Lagrangian for the system is formulated as

L=T-V (5)

To obtain the equation of the motion of the manipulator, Hamilton extended principle is used as described in eqn. (6)

where

t1 and t2 are two arbitrary times and

Manipulating Eqn. (1) - (6) yields the equation of motion of the manipulator aswrepresents virtual work.

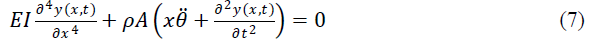The dynamic equation of the manipulator is described as

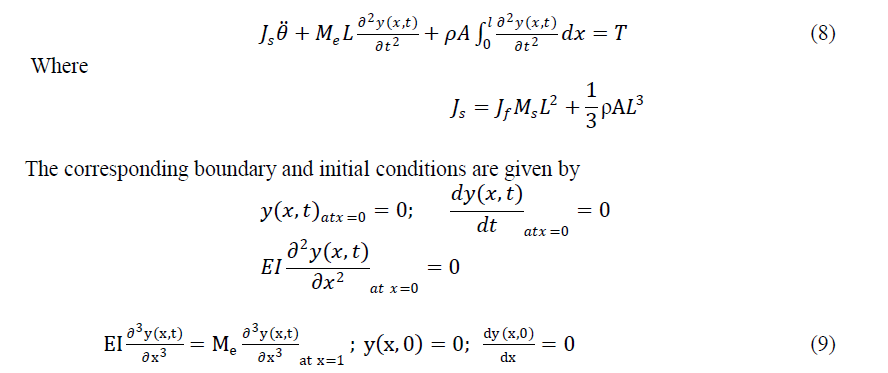Using the assumed mode method, the solution of the dynamic equation of motion of the manipulator can be obtained as linear combination of the product of the admissible function i (x) and the time-dependent generalized coordinates qi (t), as follows, where

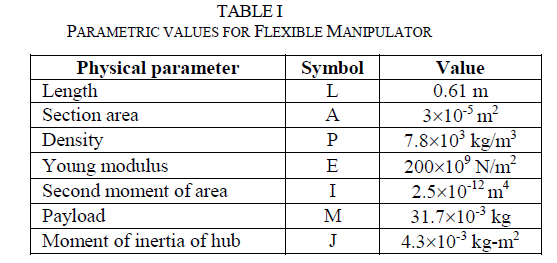Substitution of eqn. (10) into eqn. (7) by apply boundary and initial conditions of eqn. (9), the following ordinary differential equations can be derived

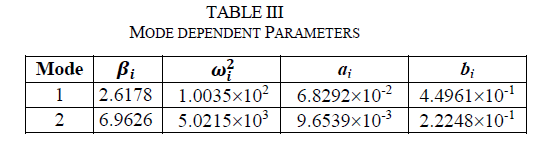III.ADVANCED CONTROLLER

The following PID, LQR and ANFIS different types of advanced controllers are discussed below

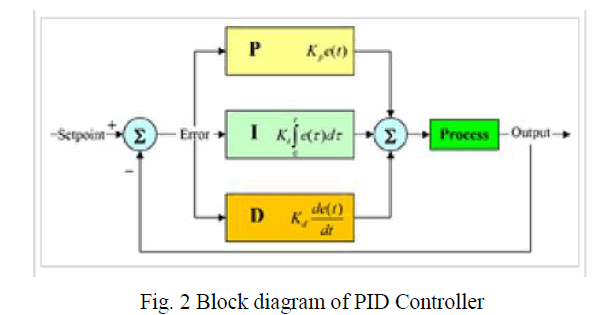
A. PROPORTIONAL-INTEGRAL-DIFFERENTIAL (PID) CONTROLLER

A PID controller is a generic loop feedback (controller) widely used in industrial control systems. A PID controller attempts to correct the error between a measured process variable and a desired set point by calculating and then instigating a corrective action that can adjust the process accordingly and rapidly, to keep the error minimal.

If the PID controller parameters are chosen incorrectly, the controlled process input can be unstable, i.e. its output diverges, with or without oscillation and is limited only by saturation or mechanical breakage. Tuning a control loop is adjustment of its control parameters to the optimum values for the desired control response.

There are several methods for tuning a PID loop. The most effective methods are generally involve the development of some form of process model, then choosing P, I and D based on the dynamic model parameters. Manual tuning methods can be relatively inefficient. The choice of the method will depend largely on whether or not the loop can be taken offline for tuning, and the response time of the system. If the system can be taken offline, the best tuning method often involve subjecting the system to a step change in input, measuring the output as a function of time, and using this response to determine the control parameters.

The PID controller calculation involves three separate parameters; the proportional, the integral and derivative values. The proportional value determines the reaction to the current error, the integral value determines the reaction based on the sum of recent errors, and the derivative value determines the reaction based on the rate at which the error has been changing. The weighted sum of these three actions is used to adjust the process via a control element such as the position of a control valve or the power supply of a heating element.

Some applications may require using only one or two modes to provide the appropriate system control. This is achieved by setting the gain of undesired control outputs to zero. A PID controller will be called a PI, PD, P or I controller in the absence of the respective control actions. PI controllers are particularly common, since derivative action is very sensitive to measurement noise, and the absence of an integral value may prevent the system from reaching its target value due to the control action.

B. LINEAR QUADRATIC REGULATOR CONTROLLER

The theory of optimal control is concerned with operating a dynamic system at minimum cost. The case where the system dynamics are described by a set of linear differential equations and the cost is described by a quadraticfunctionalis called the LQ problem. The optimal control problem for a linear multivariable system with the quadratic criterion function is one of the most common problems in linear system theory. it Is defined below:

Given the completely controllable plant

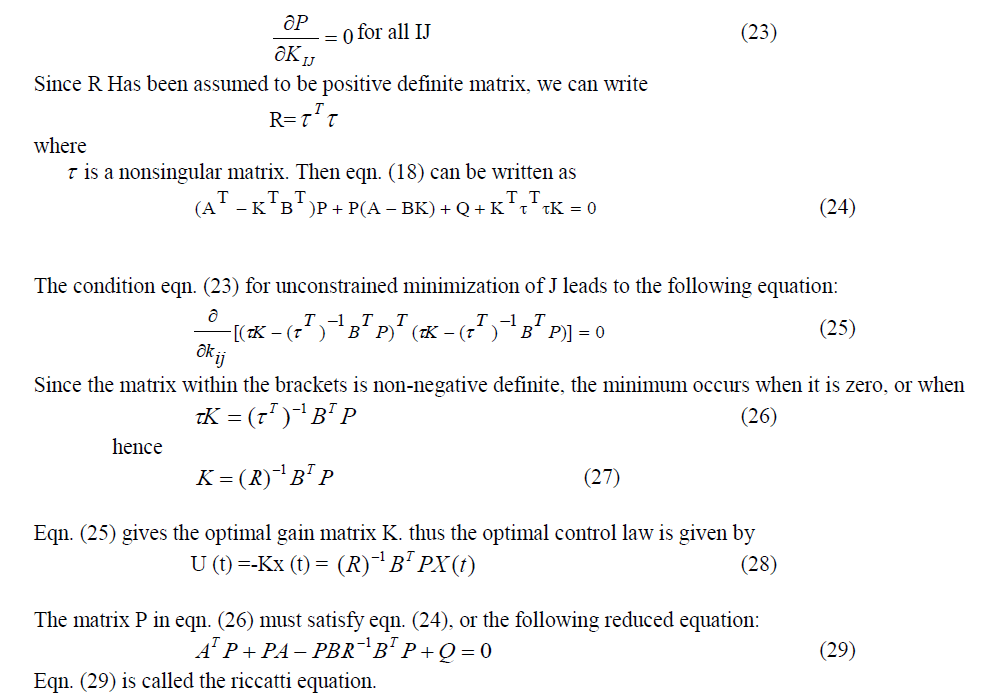We have assumed Q to be a positive definite matrix. For this choice of Q, V (x) in eqn. (19) is always negative definite; therefore the optimal feedback system is asymptotically stable. Controllability of the (A, B) pair and positive definiteness of Q are sufficient conditions for the existence of asymptotically stable optimal solution to the control problem.

The design steps may be stated as follows:

Solving the matrix riccatti eqn. (29) for the positive definite matrix P.

Substitute the matrix P into eqn. (28) and the resulting equation gives optimal control law.

This is a basic and well-known theory of optimal control. Once Q and R has been specified, the solution of eqn. (29) specifies the optimal control law eqn. (18). This yields the optimal closed-loop system.

C. ADAPTIVE NEURO-FUZZY INFERENCE SYSTEM (ANFIS) CONTROLLER

The fuzzy logic is closer in spirit to human thinking and natural language than conventional logical systems. This provides a means of converting a linguistic control strategy based on expert knowledge into an automatic control strategy. The ability of fuzzy logic to handle imprecise and inconsistent real-world data made it suitable for a wide variety of applications. In particular, the methodology of the fuzzy logic controller (FLC) appears very useful when the processes are too complex for analysis by conventional quantitative techniques or when the available sources of information are interpreted qualitatively, inexactly, or with uncertainty. Thus fuzzy logic control may be viewed as a step toward a rapprochement between conventional precise mathematical control and human – like decision making.

One of the major problems in the not so widespread use of the fuzzy logic control is the difficulty of choice and design of membership functions to suit a given problem. A systematic procedure for choosing the type of membership function and the ranges of variables in the universe of discourse is still not available. Tuning of the fuzzy controller by trial and error is often necessary to get a satisfactory performance. However, the neural networks have the capability of identification of a system by which the characteristic features of a system can be extracted from the input output data. This learning capability of the neural network can be combined with the control capabilities of a fuzzy logic system resulting in a neuro- fuzzy inference system. Recently an adaptive neuro- fuzzy inference system (ANFIS) has been proposed [7] which has been shown to have very good data prediction capabilities.

Adaptive network based fuzzy inference system serves as a basis for constructing a set of fuzzy if-then rules with appropriate membership functions to generate the stipulated input-output pairs. A Hybrid controller is a combination of ANFIS and PID controller of the system. The architecture is referred to as ANFIS, which stands for Adaptive Neuro- Fuzzy Inference System.

The ANFIS from topology point of view, an implementation of a representative fuzzy inference system using a BP neural network-like structure shown in fig. 3. It consists of five layers. Let ÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ÃÂ¯ÃÂ¿ÃÂ½ 1 denotes the output of the node i in layer l, and xi is the i th input of the ANFIS ,i=1,2,3,...p. in layer1,there is a node function M associated with every node

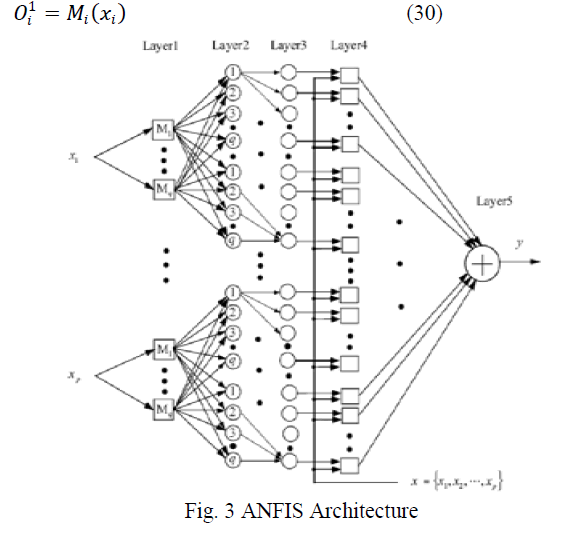The role of the node function M1, M2....Mq here is equal to that of the membership function μ(x) used in the regular fuzzy systems and q is the number of nodes for each input. Gaussian shape functions are the typical choices. The adjustable parameters that determine the positions and shapes of these node functions are referred to as his premise parameters. The output of very node in layer2 is the product of all the incoming signals.

Each node output represents the firing strength of the reasoning rules. In layer 3, each of these firing strengths of the rules is compared with the sum of all the firing strengths. Therefore, the normalized firing strengths are computed in this layer as

Layer 4 implements the sugeno-type inference system, i.e a linear combination of the input variables of the ANFIS,x1,x2,...xp plus a constant term c1,c2,c3...cp from the output of the each IF-THEN rule. The output of the node is a weighted sum of these intermediate outputs

where parameters P1, P2,...., Pp and c1 , c2 ......cp in this layer are referred to as the consequent parameters. The node in layer 5 produces the sum of its inputs i.edefuzzification process of the fuzzy system using weighted average method.

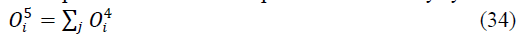Two of the difficulties with the design of any fuzzy control systems are the shape of the membership functions and choice of the fuzzy rules. In fact, the decision-making logic is the way in which the controller output is generated. It uses the input fuzzy sets, and the decision is taken according to the values of the inputs. Moreover, the knowledge base comprises knowledge of application domain and the attendant control goals. It consists of a database and a fuzzy control rule base.

A control system is said to be an adaptive fuzzy control system if either a set of fuzzy rules are used to modify membership functions and/or rules. The fuzzification uses membership functions to determine the degree of inputs. The aim of control action is to minimize the rotation error. The higher the error, the higher the control input. However, the rate of change of error also affects the value of the control input.

The fuzzification uses membership functions to determine the degree of inputs. The aim of control action is to minimize the rotation error. The higher the error, the higher the control input. However, the rate of change of error also affects the value of the control input. In the fuzzy logic controller, error is used in control rules as linguistic variables This is defined as:

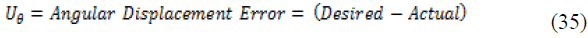In adaptive network based fuzzy inference system (ANFIS), number and type of membership functions are created by user. Then fuzzy inference system rule base is obtained automatically by ANFIS. Gauss type membership functions are used for fuzzy inputs in fuzzification process of the system. Sugeno type fuzzy inference system is adopted so these outputs by given training and checking data sets.

IV.SIMULATION RESULTS AND DISCUSSION

In this paper simulation is done for two modes of operation of single flexible-link manipulator. The reason for choosing two these modes is to show the controller conformance with different state of the single flexible-link manipulator. The two mode of performance is observed by using the PID, LQR and ANFIS controllers design. To eliminate the link vibrations at end point a controller which is combination of ANFIS and PID controller has been applied. The training of the ANFIS has been carried out by using adaptive learning algorithm.

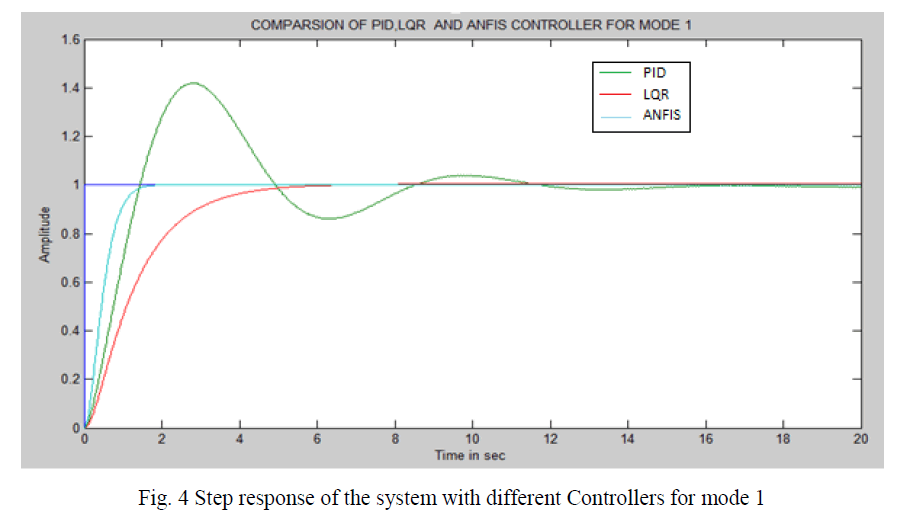
The simulation performance of the single flexible link manipulator with mode 1 and mode 2 step response operations are shown in the following fig. 4 and fig. 5 respectively.

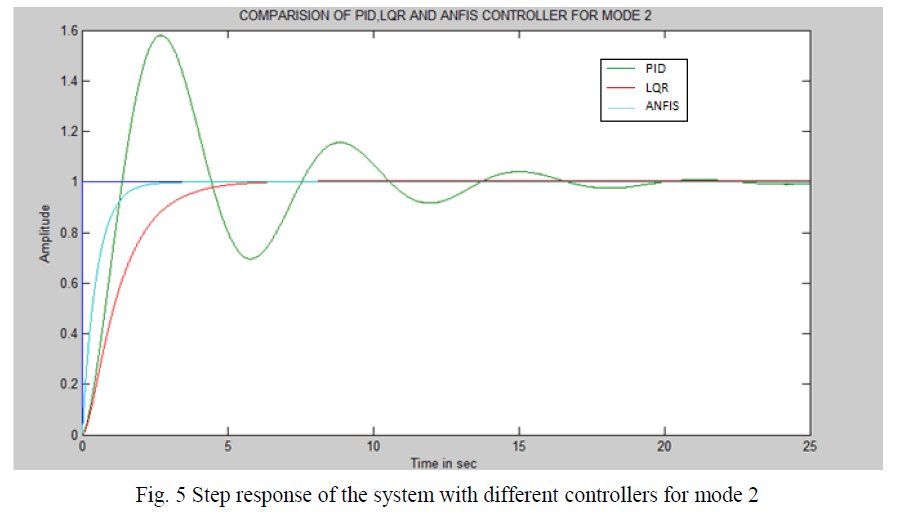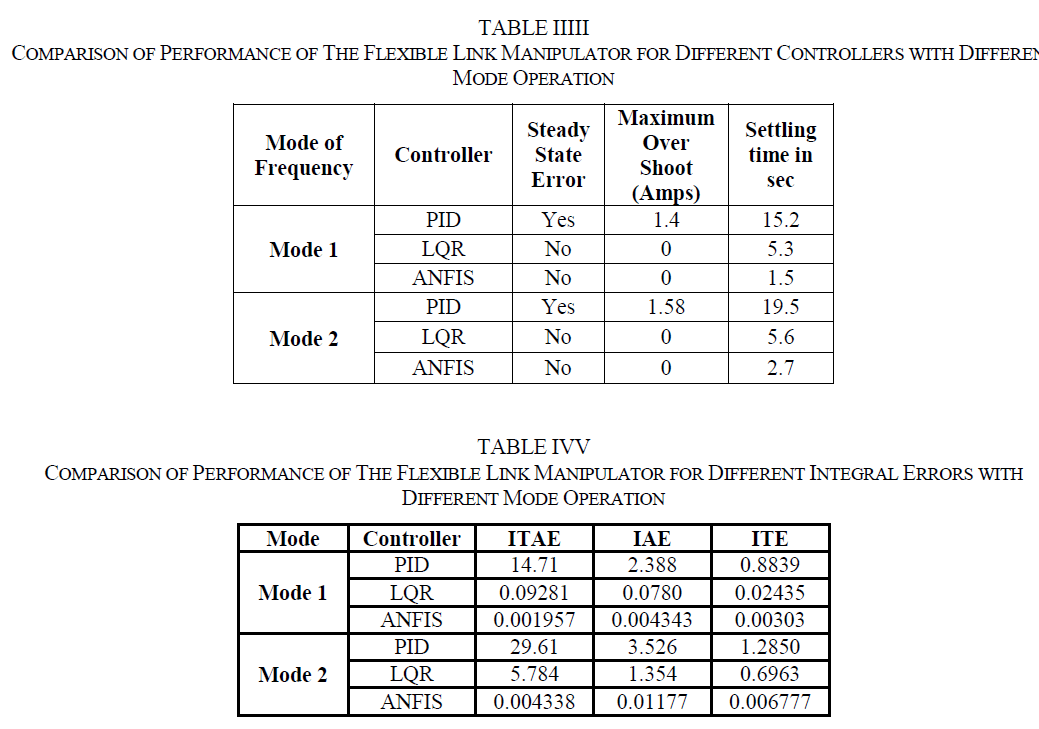
The Single Flexible Link Manipulator performance observed the steady state error, maximum over shoot in amperes and settling time in seconds with the different controllers with different mode operations and is shown in Table III. It has been observed that the stead state error and maximum over shoot eliminated with the advanced controllers LQR and ANFIS for the both the mode of operation whereas the minimum settling time achieved with the help of the ANFIS controller which has been built on the fuzzy and PID controllers. The Table IV shows the integral of Time Absolute Error (ITAE), Integrated Absolute Error (IAE) and Integrated Time Error (ITE) of the each controller and as well as the each mode of operation. It has been observe red from the Table IV, all the integral errors are very less when the controller is ANFIS in both mode of operation of step response of the single flexible link manipulator.

V.CONCLUSION

In this paper, it has been observed that the PID controller doesn’t create a suitable step response for the system. Intense transient oscillation and high over shoot are the shortcoming of such controller. Moreover the parameters of this controller are constant, no adaption with system dynamical changes. In LQR controller, even though there is no over shoot settling time is somewhat higher. With ANFIS control, the amplitude of oscillation around zero for mode 1 is about .001 and damp out after sometime, the amplitude of oscillation around zero for mode 2 is about 0.0025. Since the amplitude of oscillation persists and in order improves the transient response of the system, an ANFIS controller has been designed and simulated along with the system. It is clear that with ANFIS control the vibration of the single link flexible manipulator has been reduced.

References

KorayemM. H. and Basu A., Formulation and numerical solution of elastic robot dynamics motion with maximum load carryingcapacity,Robotica, Vol. 12, pp. 253-261, 1999.

Cheng W. and Wen J. T., ÃÂ¢Ãâ¬Ãâ¢A neural controller for the tracking control of flexible armsÃÂ¢Ãâ¬Ãâ,IEEE International Conference on Neural Network,Vol. 2, pp. 749-754, 1993.

Donne J. D. andOzguner U., ÃÂ¢Ãâ¬Ãâ¢Neural control of a flexible-link manipulatorÃÂ¢Ãâ¬Ãâ,IEEE International Conference on Neural Network, Vol. 4, pp.2327-2332, 1994.

Lee C. H. and Teng C. C., ÃÂ¢Ãâ¬Ãâ¢Identification and Control of dynamic systems using recurrent fuzzy neural networksÃÂ¢Ãâ¬Ãâ,IEEE Transactions onFuzzy Systems, Vol. 8, No. 4, pp. 349-366, 2000.

Nakanishi J. and Schaal S., ÃÂ¢Ãâ¬Ãâ¢Feedback error learning and nonlinear adaptive controlÃÂ¢Ãâ¬Ãâ, Neural Network, Vol. 17, No. 10, pp. 1453-1465, 004.

Todd Newton R. and YangshengXu, ÃÂ¢Ãâ¬Ãâ¢Real-time implementation of Neural Network learning control in a flexible space manipulatorÃÂ¢Ãâ¬Ãâ,IEEEInternational Conference Robotics Automation, pp. 135- 141, 1993.

Tain, L. and Collins C., ÃÂ¢Ãâ¬Ãâ¢Adaptive neuro-fuzzy control of a flexible manipulator,ÃÂ¢Ãâ¬Ãâ Mechatronics, Vol. 15, No. 10, pp. 1305-1320, 2005.

Torfs D. E., Vuerinckx R., SeweversJ. andSchoukens J., ÃÂ¢Ãâ¬Ãâ¢Comparison of two feed forward design methods aiming at accurate trajectoryracking of the end point of a flexible robot armÃÂ¢Ãâ¬Ãâ, IEEE Transactions Control Systems, Vol. 6, No.1, pp. 2-14, 1998.

Talebi H. A., KhorasaniK. and Patel R. V., ÃÂ¢Ãâ¬Ãâ¢Neural network based control schemes for flexible-link manipulator: Simulations andexperimentsÃÂ¢Ãâ¬Ãâ,Neural networks, Vol. 11, No. 7-8, pp. 1357-1377, 1998.

Farivar F., AliyariShoorehdeli M.,TeshnehlabM. andNekoui M. A., ÃÂ¢Ãâ¬Ãâ¢Hybrid control of flexible manipulatorÃÂ¢Ãâ¬Ãâ, Journal of Applied Sciences,Vol. 9, No. 4, pp. 639-650, 2009.