Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Performance Evaluation of DWTand DT-CWT with SPIHT Progressive Image Coding for Natural Image Compression

S. A. Wagh1, S. O. Rajankar2, D. G. Ganage3, O. S. Rajankar4
  1. PG Student, Department of E&TC Engineering, Sinhgad College of Engineering, Pune, India
  2. Assistant Professor, Department of E&TC Engineering, Sinhgad College of Engineering, Pune, India
  3. Assistant Professor, Department of E&TC Engineering, Sinhgad College of Engineering, Pune, India
  4. Principal, Dnyanganga Polytechnic, Narhe, Pune, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Wavelet based analysis plays a wide vital role in the image processing applications such as an image compression. The Set Partitioning Hierarchical Trees (SPIHT) is a lossy compression method that uses the progressive coding technique of an image to compress in the specified level. Decomposing the image at various levels by using Discrete Wavelet Transform (DWT) or Dual-Tree Complex Wavelet Transform (DT-CWT), then SPIHT algorithm are used to encode the larger magnitude coefficients of insignificant regions of an image with less number of bits. The performance of this algorithm is verified by achieving high peak signal to noise ratio (PSNR) for better compression levels with fewer numbers of bits per pixel. The result shows that at 40 to 70% of compression, a very high value of PSNR can achieve.

Keywords
Image Compression, DWT, DT-CWT, SPIHT, PSNR

INTRODUCTION
Digital image compression is to represent images with less data by reducing the redundancy of the image data in order to save storage cost and transmission time requirement. Without compression, file size is significantly larger, usually several megabytes, but with compression it is possible to reduce file size to 10 to 20 percent from the original without noticeable loss in quality [1]. In case of image compression, they are generally classified as, lossless or lossy. In lossless compression schemes, the reconstructed image, after compression, is numerically identical to the original image. However lossless compression can only achieve a modest amount of compression. Lossless compression is sometimes preferred for artificial images such as drawings or comics. It may also be preferred for high value content, such as still images or scan images. This is because lossy compression methods, especially when used at low bit rates; introduce compression artifacts [2].
An image reconstructed following lossy compression contains degradation relative to the original. Often this is because the compression scheme completely discards redundant information. However, lossy schemes are capable of achieving much higher compression [2]. Lossy methods are suitable for natural images such as photos where small loss of quality is acceptable to achieve a reduction in bit rate. The lossy compression produces images which is visually lossless. The basic measure for the performance of a compression algorithm is compression ratio. In lossy compression scheme, the image compression algorithm should achieve a trade-off between compression ratio and image quality. Higher compression ratios will produce lower image quality and vice versa [3]. Quality andcompression can also vary according to input image characteristics and content [3].
This paper is organized as follow: Section I gives the introduction of image compression. Section II describes the image compression process flow. Section III describes the DWT and DT-CWT used for image decomposition. Section IV explores the SPIHT image encoding scheme. Section V shows the performance ofproposed techniqueand the lastsection VI concludes the paper and followed by thereferences.

IMAGE COMPRESSION PROCESS FLOW
The DWT and DT-CWT based image compression method using progressive SPIHT encoding and decoding is shown in the Fig.1 operates by transforming data to remove redundancy.
On input image DWT with bior4.4 wavelet or Q-shift DT-CWT is used for image decomposition. Because of the superior energy compaction properties and correspondence with human visual system, wavelet compression methods have produced superior objective and subjective results.
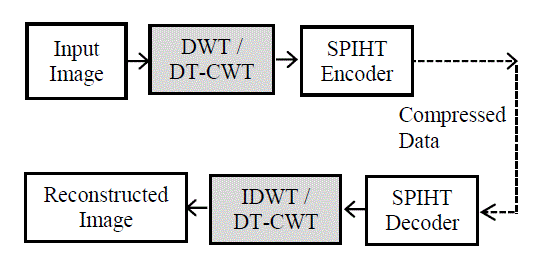
image
Fig. 1 Image compression process flow
Since wavelet basis consists of functions with both for high frequencies and low frequencies, large smooth areas of an image may be represented with very few bits. DWT & DT-CWT which produces a multi-scale image decomposition by using filtering and subsampling, a result in the form of the dyadic approach for effectively revealing data redundancy in several scales. According to image compression process flow, first image is decomposed using DWT or DT-CWT followed by a SPIHT coding process. The SPIHT coding algorithm will be used to encode the wavelet coefficients. Output of SPIHT coder is compressed image. Now reverse processing is carried out for decomposition part to obtain the reconstructed image. The SPIHT decoder will be used to decode the encoded coefficients and with inverse DWT or DT-CWT used to get the reconstructed image

WAVELET TRANSFORM
A. DWT
In the DWT, an image signal/image can be analysed by passing it through an analysis filter bank followed by decimation operation. The analysis bank consists of a LPF and HPF at each decomposition stage. When the signal passes through these filters, it splits into two bands. The LPF, which corresponds to an average operation, extracts the coarse information of the signal. The HPF, which corresponds to a differencing operation, extracts the detail information of the signal. The output of filtering operation is then decimated by two. A 2-D transform is accomplished by performing two separate 1-D transforms [4].
First, the image is filtered using LPF along the row and decimated by two for getting the low frequency components of row. But since the LPF is a half band filter, the output data contains frequencies only in the first half of the original frequency range. So, by Shannon’s sampling theorem, they can be subsampled or decimated by two, so that the output data contains only half the original number of samples. Now, the HPF filter is applied for the same row of data, and simultaneously the high pass components are separated, and placed by the side of the low pass components. This procedure is done for the all rows. Next, the filtering is done for sub-image to each column and decimated by two. The resulting is 2-D array of coefficients of four bands. This operation splits the image into four bands, namely LL, LH, HL and HH respectively as shown in Fig. 2.
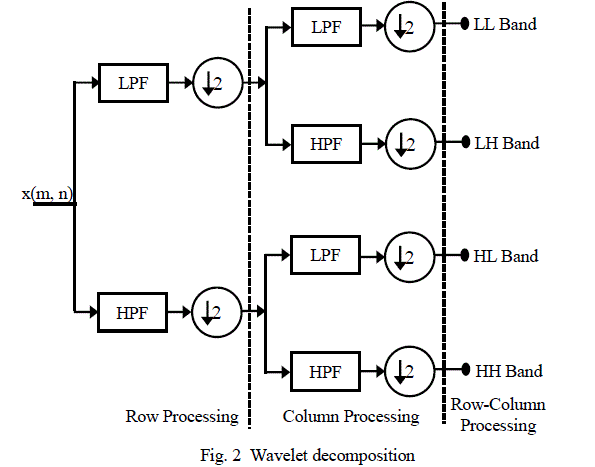image
Although Image compression algorithms based on DWT provide high coding efficiency for natural (smooth) images, the standard DWT has three major disadvantages that weaken its application. These disadvantages such as lack of shift invariance, poor directional selectivity and absence of phase information[4].
B. DT-CWT
The DT-CWT also improves PSNR and the definition of reconstruction image compared those obtained from DWT. The DTCWT, proposed by Kingsbury in 1999, has the following properties [5] [6]:
a) Approximate shift invariance
b) Good directional selectivity in 2-dimensions
c) Perfect reconstruction using short linear phase filters
d) Limited redundancy
One of the shortcomings of general DWT is shift variance. However the DT-CWT overcomes this shortcoming which has approximate shift invariance. On the other side, it also has better directional selectivity mentioned above. There are two filter banks to perform 1-D DT-CWT, so DT-CWT implements two real DWTs in parallel on the same signal, as shown in Fig.3. The upper tree gives the real part of complex transform while the lower tree gives the imaginary part [7].
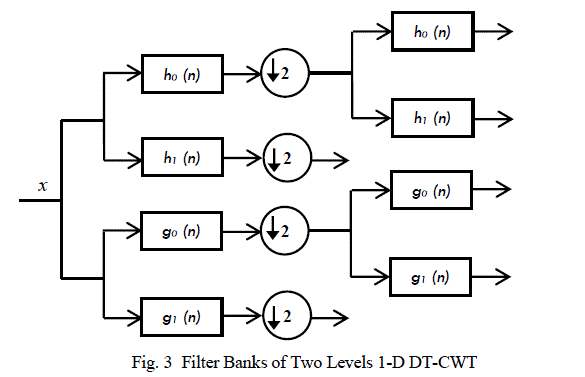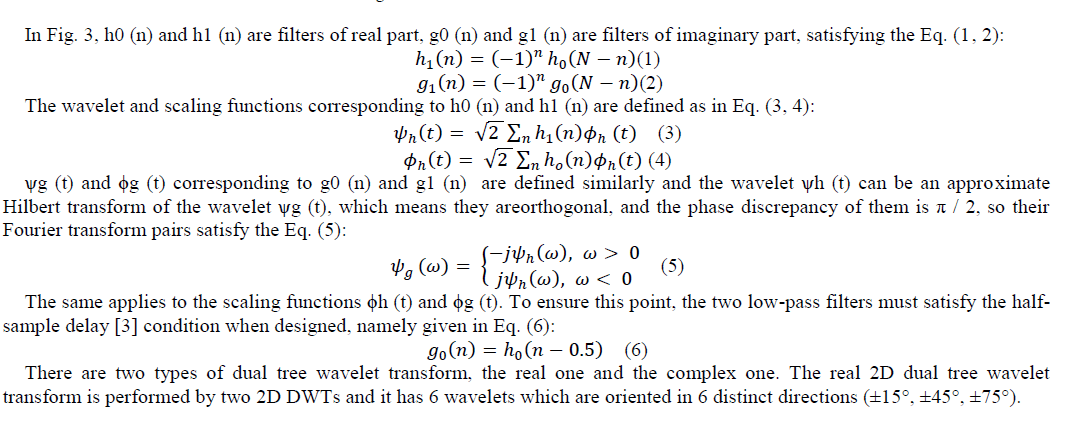image
image

SPIHT ENCODING
SPIHT stands for Set Partitioning in Hierarchical Trees. SPIHT algorithm, introduced by Said and Pearlman in 1993, is a highly advanced version of the EZW algorithm [8]. The term Set Partitioning refers to the way these quadtrees divide or partition and the wavelet transforms at a given threshold
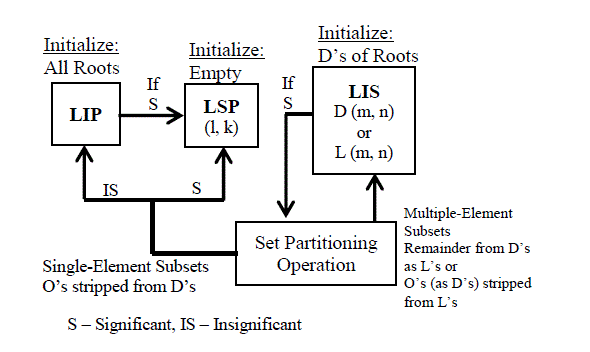
image
Fig. 4SPIHT algorithm
The SPIHT algorithm operates on a wavelet-transformed image with equal length and width of an integer power of 2. It encodes the wavelet coefficients in a way that uses a hierarchical organization of the coefficients. This encoding sends highorder bits of coefficients before low order bits. It is a very fast coding/decoding (nearly symmetric) algorithm [9].
The SPIHT multistage encoding process employs three lists and sets that will be used to keep track of important pixels [10]:
(a) List of Insignificant Pixels (LIP) contains individual coefficients that have magnitudes smaller than the threshold.
(b) List of Insignificant Sets (LIS) contains sets of wavelet coefficients that are defined by tree structures and found to have magnitudes smaller than the threshold (insignificant).
(c) List of Significant Pixels (LSP) is a list of pixels found to have magnitudes larger than the threshold (significant).
In Fig. 4 the term significant pixel is used to indicate that the magnitude of a pixel exceeds or equals the current threshold. An insignificant pixel is a pixel whose magnitude is less than the current threshold. An insignificant set can be one of two types ofsets. The set H contains all the pixels in the last level of the wavelet transform that was performed, including the coarse and detail coefficients. The sets can represent the corresponding tree representations as: O (i, j): set of coordinates of all offspring of node (i, j), D (i, j): set of coordinates of all descendants of node (i, j), H (i, j): set of all tree roots (nodes in the highest pyramid level) andL (i, j): D (i, j) – O (i, j).
A general procedure for the code is as follows [8]-[11]:
Step 1: Initialize the threshold and order list
Assign coefficients of all the root node in low-pass sub-band to LIP, all the trees (designated as D-tree) are assigned to LIS and LSP is initialized to be an empty set.
Step 2: Sorting Pass
The aim is to encode the important coefficient of current bit. There are two main steps:
a) Check all the wavelet coefficients in LIP to determine whether they are important coefficients:
• If it is yes, then output “1” and the sign bit, positive or negative sign bits of wavelet coefficients are represented by “1” and “0”, and then remove the coefficient from LIP and add to the end of order list LSP.
• If it is not, we do not need to remove it from the list of LIP and give a direct output of “0”.
b) According to the type of trees, we shall check all the important trees in LIS:
• D-type tree: If the tree is important, we need to give output of “1”, and then encode the coefficients on sub-node. If the coefficient of child node is important, we need to make output of “1” and sign bit, then move it into LSP. If the coefficient of child node is not important, the output shall be “0”, and then move it in LIP. If the child node has offspring, put the tree to the end of LIS list and regard it as L-tree. If the tree is not important, then we need to make output of “0”.
• L-type tree: If the tree is important, then make output of “1” and move each child node to the end of LIS as a D-tree, then delete the parent tree from LIS. If the tree is not important, then the output shall be “0”. Algorithm provides that if there are coefficients which can make inspections on, the SPIHT must check the coefficients in LIP; if there is no coefficient for inspection in LIP, then remove the untreated coefficients from LIS and put in LIP.
Step 3: Refinement Pass
The aim is output but not the improving position of important factor in generated in the process of scanning. For each node (i, j) in LSP, if (i, j) is not just added during the scanning process, then absolute value |Ci, j| of the output of this node coefficient can be transmitted.
Step 4: Update the threshold by decrement n by 1 and conduct the next level coding (back to step 2).

RESULTS
We conducted several simulations on a group of images in order to test the effect of the coding algorithm. The results are mostly measured via PSNR computed from MSE. By varying bits per pixel (bpp) in the image, compression ratio and PSNR is measured on “girl face and woman” image with dimensions 512×512 pixels. The measurements were performed for a decomposition of depth 3, using bior4.4 wavelet for DWT and Q-shift DT-CWT with 13/19 tap filter in first stage and 14/14 tap filter beyond level one. The results are presented in Table I and Table II.Fig.5 and Fig.6 shows the reconstructed image at various bit rates respectively.
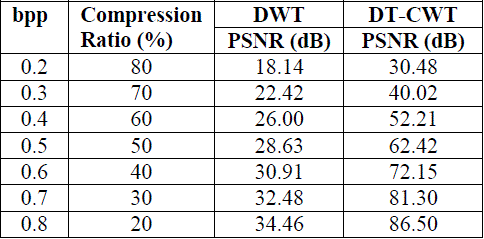
image
TABLE I COMPRESSION PERFORMANCE OF “GIRLFACE.BMP”
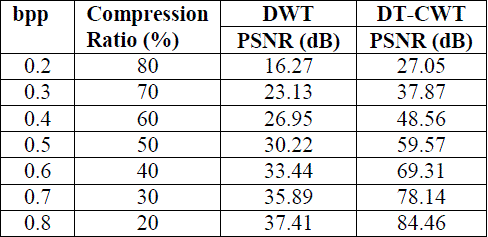
image
TABLE II COMPRESSION PERFORMANCE OF “WOMAN.BMP”

CONCLUSION
In this paper, we presented a system for an image compression using DWT or DT-CWT with SPIHT progressive coding technique. DT-CWT with SPIHT coding reconstructs the image at 70% of compression ratio whereas DWT with SPIHT coding reconstructs the image at 40% of compression ratio. DT-CWT improves the value of PSNR and compression ratio far better than DWT. Which means it can improve the performance of compression and coding. But cost of computational complexity using DT-CWT is approximately twice that of DWT. In the future much more effort must be emerged in order to make the coder more better for visual quality at high compression ratio using dual-tree complex wavelet transform with slightly modification in traditional SPIHT.

ACKNOWLEDGMENT
We would like to thank Dr. A. D. Jadhav, Head (PG Programmes), Dept. of E&TC, SCOE, Pune and Dr. S. D. Lokhande (Principal), SCOE, Pune for providing necessary guidance and infrastructure for completion of work.
image
Fig. 5 Reconstructed girlface image(a) DWT and (b) DTCWTFig. 6 Reconstructed woman image(a) DWT and (b) DTCWT

References