pH-metric Investigation on Mixed-Ligand Complexes of Ca(II), Mg(II) and Zn(II) with L-Dopa and 1, 10-Phenanthroline in Propylene glycol -Water Mixtures

Abstract

The stability constants of ternary complexes of Ca(II), Mg(II) and Zn(II) with L-dopa as primary ligands and 1, 10-phenantbroline as a secondary ligand were determined pH-metrically. The study was conducted in varying concentrations (0-60% v/v) of propylene glycol-water mixtures and at an ionic strength of 0.16 mol L-1 using NaCl as an electrolyte at 303.0 K. Values of log X and Δ log K was discussed on the basis of statistical considerations and the nature of the species formed. The formation of various ternary species was established by modeling studies using the computer program MINIQUAD75. The formation and distribution of different species with relative concentrations of metal and ligands (M:L:X = 1.0:2.5:2.5, 1.0:2.5:5.0, 1.0:5.0:2.5) with varying pH were represented in the form of distribution diagrams. Influence of the solvent on the speciation was discussed based on the dielectric constant of the medium. The stability of the mixed ligand complexes are discussed in terms of the molecular structure of dopa and phen as well as the nature of the metal ion.

Keywords

Ternary complexes, Speciation, pH-metric study, L-dopa, 1, 10-phenantbroline

Introduction

L-Dopa (dopa) has been used for the treatment of Parkinson disease. For its better therapeutic effect it must be administered daily in high doses, for a long time. Considerable proportion of it is decarboxylated in the peripheral regions, and accordingly it does not reach the brain, where its action is to be increased. To avoid this extra cerebral decarboxylation, L-dopa is generally used in combination with peripheral dopa decarboxylase inhibitors. Rajan et al., investigated an alternative possibility, of applying metal complexes of dopa [1]. They also dealt with the coordination chemistry aspects of ternary metal complexes of dopa [2,3]. Clearly, the metal complexes that may be of therapeutic importance are those in which metal ion is coordinated to the amino acid side-chain at physiological pH.

The protonation equilibria and complex forming properties of dopa and phen with certain transition metal ions were studied in this laboratory [4,5,6,7,8]. Subsequently the stability and bonding conditions relating to the complexes formed in the ternary systems of dopa and phen were also dealt with results. Basing on these it is concluded that the L-dopa ligand is an ambidentate ligand in these ternary complexes which can bound to the metal ion via the (N,O) donor groups at physiological pH.

In this work we report speciation of the ternary complexes of Ca(II), Mg(II) and Zn(II) with L-dopa and l,10-phenanthroline in PG-water mixtures. The pH-metric method was used to determine the stoichiometries and stability constants of the ternary complexes.

Experimental

0.05 mol L^-1 solutions of L-Dopa (Loba, India) and 1,10-phenanthroline mono hydrate (Finar, India) were prepared in deionised triple-distilled water by maintaining 0.05 mol L^-1 concentration of hydrochloric acid to increase the solubility. 0.2 mol L^-1 stock solution was prepared from Hydrochloric acid (Qualigens, India). 1,2-propanediol (Finar, India) was used as received. 2 mol L^-1 Sodium chloride (Qualigens, India) was prepared to maintain the ionic strength in the titrand. 0.1 mol L^-1 solutions of Ca(II), Mg(II) and Zn(II) chlorides were prepared by dissolving G.R. Grade (Merck, India) salts in triple distilled water maintaining 0.05 mol L^-1 concentration of HCl to suppresses the hydrolysis of metal salts. Sodium hydroxide (Qualigens, India) of 0.4 mol L^-1 and Hydrochloric acid (Qualigens, India) of 0.2 mol L^-1 were prepared. All the solutions were standardized by standard methods. To assess the errors that might have crept into the determination of the concentrations, the data were subjected to analysis of variance of one way classification [9]. The strengths of alkali and mineral acid were determined using the Gran plot method [10,11].

Procedure

ELICO (Model LI-120) pH meter of readability 0.01 was used for pH metric titrations. The effect of variations in asymmetry, liquid junction potential, activity coefficient, sodium ion error and dissolved carbon dioxide on the response of glass electrode were accounted for in the form of correction factor [12,13,14]. For the determination of stability constants of ternary species, the establishment of equilibration of the glass electrode was checked by titrating strong acid against alkali at regular intervals. The calomel electrode was refilled with PG-water mixture of equivalent composition as that of the titrand. All the titrations were performed pH metrically at 303.0±0.1 K in media containing varying concentrations (0-60% v/v) of PG-water mixtures. Titrations were carried out in the presence of different relative concentrations of the metal ion (M) to dopa (L) and phen (X) with 0.4 mol L^-1 sodium hydroxide. The concentrations of the ingredients are given in Table 1. The details of experimental procedure and titration assembly are given elsewheare [15].

Results and Discussion

Modeling of Chemical Speciation

A preliminary investigation of alkalimetric titrations of mixtures containing different mole ratios of dopa and phen in the presence of mineral acid and inert electrolyte inferred that no condensed species were formed. The best fit models were chosen based on the statistical parameters [14] like χ², R-factor, skewness and kurtosis given in Table 2. The ternary complex species detected are MLXH, MLX₂H, MLX and ML₂X for Ca(II) and Zn(II) and MLXH, MLX, MLX₂ and ML₂X for Mg(II). A very low standard deviation (SD) in log values of overall stability constants (log β) indicates the precision of these parameters. The small values of U_corr (sum of squares of the deviations in the concentrations of the ligands and the hydrogen ion at all the experimental points corrected for degrees of freedom) indicate that the models represent the experimental data. Small values of mean, standard deviation and mean deviation for these systems corroborate that the residuals are around a zero mean with little dispersion. For an ideal normal distribution, the values of kurtosis and skewness should be three and zero, respectively. The kurtosis values in the present study of Ca(II) and Mg(II) indicate that most of the residuals are very nearer to mesokurtic and a few form leptokurtic patterns while Zn(II) indicates leptokurtic patterns. The values of skewness recorded in Table 2 are between –0.49 and 1.64. These data indicates that the residuals form a part of normal distribution. Hence the least–squares method can be applied to the present data. The sufficiency of the model is further evident from the low crystallographic R-values recorded.

Effect of Dielectric Constant on the Stability of Ternary Complexes

PG is an amphiprotic solvent. It is a structure former and it enhances the water structure in PG-water mixtures. Hence it removes water from the coordination sphere of the metal ions, making them more reactive towards the ligands. As a result, the stability of the complexes is expected to increase. At the same time, it is a coordinating solvent which competes with the ligands for coordinating with the metals. This decreases the stability of the complexes. Hence, the stability of the complexes is expected to either increase or decrease linearly. The variation of overall stability constants with co-solvent content depends upon the electrostatic and the non-electrostatic factors. Born’s classical treatment holds good in accounting for the electrostatic contribution to the free energy change [16]. According to this treatment, the energy of electrostatic interaction is related to dielectric constant. Hence, the log β values should vary linearly as a function of reciprocal of the dielectric constant (1/D) of the medium, which is observed in the present study (Figure 1). The linear variation indicates that the electrostatic forces are dominating the equilibrium process under the present experimental conditions. The linear increase in the stability of the complexes indicates the dominance of structure forming nature of PG over its complexing ability. The cation stabilizing nature of co solvents, specific solvent-water interactions, charge dispersion and specific interactions of co solvent with solute (indicated by the changes in the solubility of different species in the aqua-organic mixtures) account for the little deviation of linear relationship.

Stability of Ternary Complexes

The complexes formed can be characterized with the following general equilibrium process and stability constant:

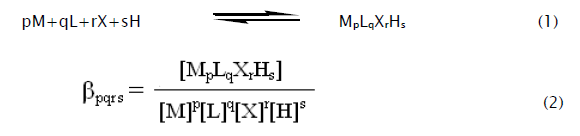
The stability constants defined by Eq. (2) were calculated from the pH-metric titration curves in the usual way with the aid of the computer programme MINIQUAD75 [17]. The computer program SCPHD [18] was used to calculate the correction factor. During the refinement of ternary systems, the correction factor, protonation constant and binary formation constant of dopa and phen were fixed. The variation of stability constants with the dielectric constant of the medium was analyzed on the basis of electrostatic/nonelectrostatic, solute-solute and solute –solvent interactions.

The formation of mononuclear unprotonated binary and ternary complexes from a mixture of metal ion (M) and primary (L) and secondary (X) ligands can be shown as the equilibria given in Equilibria (3)

The change in the stability of the ternary complexes as compared to their binary analogues was quantified based on the disproportion constant (log X) given by Equation [19,20,21,22] which corresponds to equation (5).

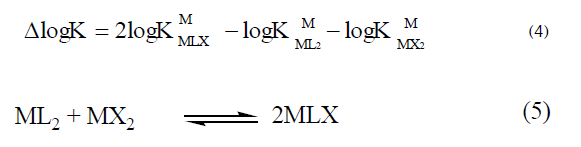
Under the equilibrium conditions one can expect the formation of 50% ternary complexes and 25% each of the binary complexes statistically and the value of log X shall be 0.6, [23] a value greater than these accounts for the extra stability of MLX.

Another approach to quantify the stability of ternary complexes was based on the difference in stability (Δ log K) for the reactions ML with X and M_(aq) with L and X, [20-24] where L is the primary ligand (Dopa) and X is the secondary ligand (Phen). It is compared with that calculated purely on the statistical grounds as given in Equation (6)

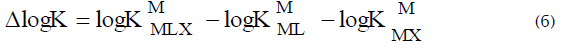
The electrostatic theory of binary complex formation and statistical arguments suggest the availability of additional coordination positions of the hydrated metal ion for the first ligand than for the second. Hence, the usual order of stability 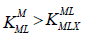applies. This suggests that Δ log K should be negative, although several exceptions have been found. [25] .

The statistical values of Δ log K for bi-dentate ligands L and X are –0.4, –0.6 and between –0.9 and –0.3 for octahedral, square planar and distorted octahedral complexes, respectively. Negative values of Δ log K can be understood as the secondary ligand forms a more stable complex with ML than hydrated metal ion. Whenever the experimental values of Δ log K exceed the statistical values, it can be inferred that the ternary complex is formed as a result of interaction of ML with X or MX with L. Δ log K values of ternary complexes are positive for O-donors (malonic acid, pyrocatechol etc.), [20] negative for N-donors (ethylene diamine) and intermediate or negative for amino acids with both N and O coordination sites. [26,27] However, a very high negative value (–2.3) for Cu(ethylene diamine)(iminodiacetic acid) and a positive value (0.82) for Cu(o-phen)-(6,7-dihydroxynaphthalene-2-sulphonate) were also observed.

The log X and Δ log K values calculated from binary and ternary complexes are included in Table 3. The equations for the calculation of Δ log K and log X are given in Table 4. These values could not be calculated for some systems due to the absence of relevant binary species. In the present study, the log X values range from -1.93 to 23.48 and these values are found to be higher than those expected on the basis of statistics (0.6). These higher values account for the extra stability of the ternary complexes. Δ log K values are in the range from -4.11 to 11.62 which indicate that the ternary complexes formed by the Ca(II) and Mg(II) were more stable compared to Zn(II). The reason for the extra stability of these complexes may be due to interactions outside the coordination sphere such as the formation of hydrogen bonds between the coordinated ligands, charge neutralization, chelate effect and stacking interactions. [28]

Effect of Influential parameters on stability Constants

Any variation in the parameters like concentration of ingredients affects the magnitude of equilibrium constants. Such parameters are called influential parameters. In order to rely upon the best chemical model for critical evaluation and application under varied experimental conditions with different accuracies of data acquisition, an investigation was made by introducing pessimistic errors in the concentrations of alkali, acid, ligands, metal ions and correction factors. The results of typical samples given in Table 5 emphasise that the errors in the concentrations of alkali and acid affect the stability constant more than those of the ligands and metal ion.

Chemical Speciation

Distribution diagrams drawn using the formation constants of the best fit model are shown in Figure 2 which contain protonated and unprotonated species like MLXH, MLX2H, MLX and ML₂X for Ca(II) and Zn(II) and MLXH, MLX, MLX₂ and ML₂X for Mg(II). The distribution diagrams indicate the relative abundance of various forms of metal (chemical speciation) at different pH and dielectric conditions. A stable ternary complex shall be responsible for metal ion transportation in biological systems and the weak binary metal complexes make the essential metals bioavailable. The increased concentrations of complexing agents make the essential metal ions unavailable due to the formation of stable binary metal complexes. The formation of the complex species can be represented by the following equilibria.

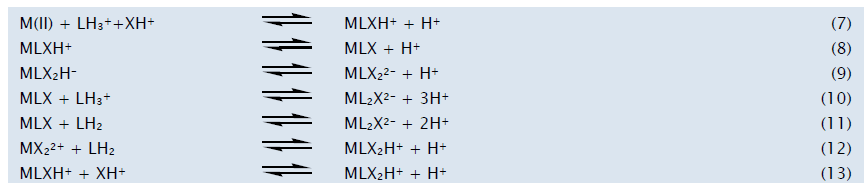
Some typical distribution diagrams in 20% PG-water mixture are shown in Figure 2. Figure 2a shows the formation of dopa-Ca(II)-phen complexes, MLXH, MLX₂H, MLX and ML₂X in the pH range 4.5-10.5. At lower pH concentration of MLXH species is high (Equilibtium 7). As the concentration of MLXH decreases with increasing the concentration of MLX₂H (Equilibtium 13). As the pH increases the concentration of MLXH and LH₂ decreased and the concentration of MLX and ML₂X are increased (Equilibria 8,10, and 11).

Figure 2b shows the formation of dopa-Mg(II)-phen Complexes, MLXH, MLX₂, MLX, and ML₂X in the pH range 6.0-10.0. At lower pH the concentration of MLXH is high (Equilibrium 7). As the pH increases the concentration of MLXH decreases with increasing concentration of MLX₂, MLX, and ML₂X species (Equilibria 8,9,10 and 11).

Figure 2c shows the formation of dopa-Cu(II)-phen Complexes, MLXH, MLX₂H, MLX and ML₂X in the pH range 1.8-10.0. At lower pH the species MLXH has high concentration (Equilibrium 7). As the pH increases the concentration of MLXH, LH3 and XH decreased and the concentration of MLX and MLX₂H are increased (Equilibria 8 and 13). Above a pH 8.0 the concentration of MLXH and MLX species decreases with increasing ML₂X species indicating the formation of ML₂X through Equilibria 10 and 11.

Depending upon the nature of the ligands and the metal ions and based on the basic chemical knowledge the structures of the ternary complexes are proposed as shown in Figure 3. Dopa and phen form strong bidentate complexes with transition metals. Dopa at higher pH favors the (O,O) coordination. At physiological pH it is bound only through the amino acid side chain [29,30,31,32].

Conclusions

A study of the speciation of ternary complexes of Ca(II), Mg(II) and Zn(II) with dopa and Phen PG–water media reveals the compartmentalization of metabolic reactions. The following conclusions have been drawn from the modeling studies:

➢ The species detected are MLXH, MLX₂H, MLX and ML₂X for Ca(II) and Zn(II) and MLXH, MLX, MLX₂ and ML₂X for Mg(II). Where L = Dopa and X = Phen. Only these species are refined due to the restricted pH ranges and the possible active forms of ligands like LH₃⁺, LH₂ and LH^- for dopa and XH⁺ for Phen.

➢ The values of Δ log K indicate that the ternary species have extra stability compared to their binary species, may be due to the interactions outside the coordination sphere, such as the formation of hydrogen bonds between the coordinated ligands, charge neutralization, chelate effect, stacking interactions and the electrostatic interaction between non-coordinated charge groups of the ligands.

➢ The linear increase in the stabilities of ternary complexes with decreasing dielectric constants is due to the dominance of electrostatic forces.

➢ The order of the ingredients that influence the magnitudes of stability constants due to incorporation of errors is alkali > acid > Dopa > Phen> metal.

➢ The study also gives an insight into the metal availability/metal transport in biofluids and toxicity of these metals. The ternary complexes are more amenable for ‘metal transport’ because of their extra stability and the binary complexes make the ‘metal available’ in biological systems due to their decreased stability.

References

1. Rajan KS, Mainan AA, Davis JM, Dekirrnenjian H. Metal chelates of L-DOPA for improved replenishment of dopaminergic pools. Brain Res. 1976;107:317-31.
2. KS Rajan, S Mainer, JM Davis.Formation and stabilities of the ternary metal chelates of l-3,4-dihydroxyphenyl alanine (l-dopa)J Inorg Nucl Chem. 1978; 40(12):2089-2099.
3. Rajan KS, Mainer S, Davis JM. Studies on chelation of L-DOPA with metal ions and metal-ATP systems. Bio Inorg Chem. 1978;9:187-203.
4. Rao GN, Ramana KV, Rao RS. Computer augmented modeling of complexes of amino acids in aquo-organic mixtures. Part I. Acido- basic equilibria of L-alanine and L-DOPA in aquo-DMSO media. J Indian Chem Soc. 1991;68:34-41.
5. Devi KVS, Raju BR, Rao GN. Effect of dielectric constant on protonation Equlibria of L-Dopa and 1, 10 –Phenanthroline in Dioxan- Water Mixtures. Acta Chim Slov. 2010;57:398-404.
6. Devi KVS, Raju BR, Rao GN. Speciation of binary complexes of Ca(II), Mg(II) and Zn(II) with L-dopa in Dioxan-water Mixtures. Chem Speciat Bioavail. 2010;22:191-199.
7. Devi KVS, Raju BR, Rao GN. Speciation of complexes of Ca(II), Mg(II) and Zn(II) with 1, 10 –Phenan-throline in dioxan-water Mixtures. J Indian Chem Soc. 2011;88:567-571.
8. Raju BR, Devi KVS, Rao GN. Formation of binary complexes of Co(II), Ni(II) and Cu(II) with L-Dopa in dioxan-water mixtures. Bull Chem Soc Ethiop. 2011;25:43-52.
9. Rao RS, Rao GN, Computer Applications in Chemistry, Himalaya Publishing House, Mumbai: India;2005.
10. Gran G. Determination of the equivalence point in potentiometric titrations. Analyst. 1952;77:661-671.
11. Gran G. Equivalence volumes in potentiometric titrations. Anal Chim Acta 1988;206:111-123.
12. Raju BR, Devi KVS, Rao GN. Chemical speciation of Ternary Complexes of L-dopa and 1, 10-Phenanthroline with Co(II), Ni(II) and Cu(II) in low dielectric media. Chem Speciation Bioavail. 2012;24:89-96.
13. Raju BR, Devi KVS, Rao GN. Chemical Speciation of Ternary Complexes of Co(II), Ni(II) and Cu(II) with L- dopa and 1,10- phenanthroline in low dielectric media. Chin J Inorg Chem. 2012;28:785-794.
14. Srikanth B, Rao PS, Rao VSS, Sastry CK, Rao GN. Effect of micelles on chemical speciation of binary complexes of Co(II), Ni(II), Cu(II) and Zn(II) with succinic acid. J Serb Chem Soc. 2009;74:745-754.
15. Lavanya KV, Rao GN, Rajesh M, Babu MS. Micellar effect on protonation equilibria of L-arginine and L-histidine. J Indian Chem Soc. 2004;81:384-387.
16. Born M. Volume and hydration heat of ions. Z Phys. 1920;1:45-48.
17. Gans P, Sabatini A, Vacca A. An improved computer program for the computation of formation constants from potentiometricdata.Inorg Chim Acta. 1976;18:237-239.
18. Rao GN. Complex Equilibria of Biological importance in Aquo-organic media-Computer augmented modeling studies. Ph.D. Thesis, Andhra University;Visakhapatnam:India 1989.
19. Griesser R, Sigel H. Ternary complexes in solution. VIII. Complex formation between the copper(II)-2,2'-bipyridyl 1:1 complex and ligands containing oxygen and/or nitrogen donor atoms. Inorg Chem. 1970;9:1238-1243.
20. Griesser R, Sigel H. Ternary complexes in solution. XI. Complex formation between the cobalt(II)-, nickel(II)-, copper(II)-, andzinc(II)-2,2'-bipyridyl 1:1 complexes and ethylenediamine, glycinate, or pyrocatecholate. Inorg Chem. 1971;10:2229-2232.
21. Sigel H, Caraco R, Prijs B.Ternary complexes in solution. XVI. Influence of the size of the chelate rings on the stability of mixed- ligand copper(II) complexes containing aliphatic ligands. Inorg Chem. 1974;13:462-465.
22. Sigel H, Huber PR, Greisser R, Prijs B. Ternary complexes in solution. XV. Mixed-ligand copper(II) complexes with 2,2'-bipyridyl or 1,10-phenanthroline and pyrocatecholate or derivatives thereof. Inorg Chem. 1974;12:1198-1200.
23. Kida S. Investigation on Mixed Complex. I. Spectrophotometric Study of Mixed Complexes Formed by Cupric Ion and Bidentate Ligands. Bull Chem Soc Jpn. 1956;29:805-811.
24. Martin RB, Prados RJ. Some factors influencing mixed complex formation. Inorg Nucl Chem. 1974;36:1665-1670.
25. Sigel H. Ternary Cu2+ Complexes: Stability, Structure and Reactivity. Angew Chem Int Ed Engl. 1975;14:394-402.
26. Sigel H. Ternare Komplexe in Losung. Chimia. 1967;21:489-500.
27. Griesser R, Sigel H. Ternare Komplexe in Losung I I†. Einfluss von 2,2′-Bipyridyl auf die Stabilitat des Cu2+-Glycin-1:1- Komplexes. Helv Chim Acta. 1967;50:1842-1845.
28. Sakurai T, Yamauchi O, Nakahara A. Mixed Ligand Copper(II) Complexes of α-Amino Acids with Ligand-Ligand Interactions. Bull Chem Soc Jpn. 1976;49:169-173.
29. Patel VK, Bhattacharya PK. Study of copper(II) and nickel(II) ternary complexes involving tertiary amines and phenyl or hydroxylphenyl substituted amino acids.J Inorg Biochem. 1984;21:169-177.
30. Gergely A, Kiss T.Complexes of 3, 4-dihydroxyphenyl derivatives. I. Copper(II) complexes of DL-3,4-dihydroxyphenylalanine.Inorg Chim Acta. 1976;16:51-59.
31. Gergely A, Kiss T, Defik G.Complexes of 3,4-dihydroxyphenyl derivatives. II. Complex formation processes in the nickel(II)-L- DOPA and zinc(II)-L-DOPA systems. Inorg Chim Acta. 1979;36:113-120.
32. Kiss T, Defik G, Gergely A. Complexes of 3,4-dihydroxyphenyl derivatives. VII. Mixed ligand complexes of L-dopa and related compounds.Inorg Chim Acta. 1984;91:269-277.