International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Pitch Control of DFIG based Wind Energy Conversion System for Maximum Power Point Tracking

T.Salma1, R.Yokeeswaran2
  1. P.G Scholar [PSE], Dept of EEE, V.S.B. Engineering College, Karur-639111, Tamilnadu, India
  2. Assistant professor, Dept of EEE, V.S.B. Engineering College, Karur-639111, Tamilnadu, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

With the advancements in the variable speed system design and control of wind energy systems, the efficiency and energy capture of these systems is also increasing. Intelligent control techniques can play a vital role in improving the performance and the efficiency of Wind Energy Conversion Systems (WECS). This paper proposes the Pitch control of a Doubly Fed Induction Generator based wind energy system with the aim of maximizing the power output by using fuzzy controller along with Hill Climbing Search (HCS) algorithm. Pitch control is the most common means for regulating the aerodynamic torque of the wind turbine and this algorithm searches for the peak power by varying the speed in the desired direction. The generator is operated in the speed control mode with its reference speed being varied in accordance with the magnitude and direction of change of active power. The peak power points in the Power (P)-Speed (ω) curve correspond to dP/dω=0. This fact is made use of in the optimum point search algorithm. The proposed method is computationally efficient and can be easily implemented in real-time. This system is modeled using MATLAB/Simulink. Simulation results prove the efficiency of this technique.

Keywords
Wind turbine, Pitch angle, DFIG, HCS.

INTRODUCTION
In recent years, wind energy has become one of the most important and promising sources of renewable energy, which demands additional transmission capacity and better means of maintaining system reliability. Wind energy is a nonpolluting, safe renewable source. The evolution of technology related to wind systems industry leaded to the development of a generation of variable speed wind turbines that present many advantages compared to the fixed speed wind turbines. The power retrieved from wind energy systems depends on the power set point traced by maximum power point tracking.
The mechanical power from the wind turbine is affected by turbine‘s Tip Speed Ratio (TSR). It is defined as the ratio of turbine rotor tip speed to the wind speed. At optimal TSR, the maximum wind turbine efficiency occurs for a given wind speed. To maintain the optimal TSR, turbine‘s rotor speed is to be changed as the wind speed changes. Also, extracts maximum power from wind. TSR calculation requires the measured value of wind speed and turbine speed data. Wind speed measurement increases the system cost and also leads to practical difficulties. Optimal values of TSR differ from one system to another.
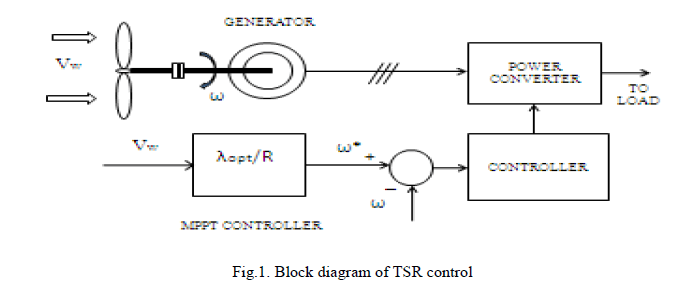image
Power Signal Feedback (PSF) needs the details of maximum power curve of the wind turbine. This curve is tracked by the control mechanisms. This curve is obtained from simulation or tests for every wind turbine. The reference power is generated either using a recorded maximum power curve or using the mechanical power equation of the wind turbine and here the wind speed or rotor speed may be used as the input. This control method increases cost of implementation and is difficult. Fig.2. shows the logic for the power signal feedback control.
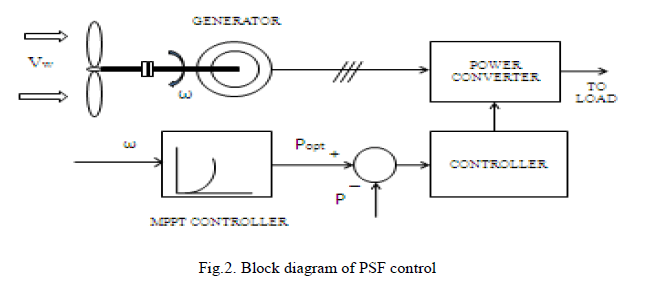image
The drawbacks of the TSR and PSF control methods are overcomed by Hill climbing search (HCS) method. The HCS control algorithm continuously searches for the peak power of the wind turbine. It can overcome some of the common problems normally associated with the other two methods. The tracking algorithm, depending upon the location of the operating point and relation between the changes in power and speed, computes the desired optimum signal in order to drive the system to the point of maximum power.
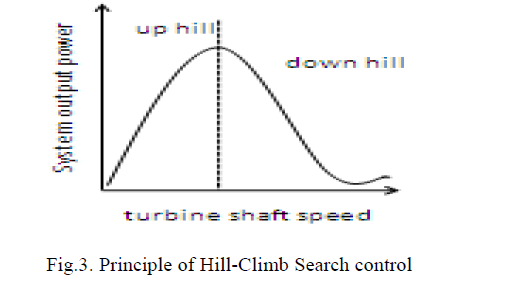image
This algorithm dynamically modifies the speed command in accordance with the magnitude and direction of change of active power in order to reach the peak power point. That is, the real power is given as the input and the optimum command (speed) signal is generated and is fed to the speed control loop of the grid side converter control. The signals proportional to Pm is computed and compared with the previous value. When the result is positive, the process is repeated for a lower speed. Based on this, the generator speed needs to be increased or decreased. For every change in operating point, the controller continues to perturb itself by running through the loop. The output power increases till dPo/dω=0 is satisfied.
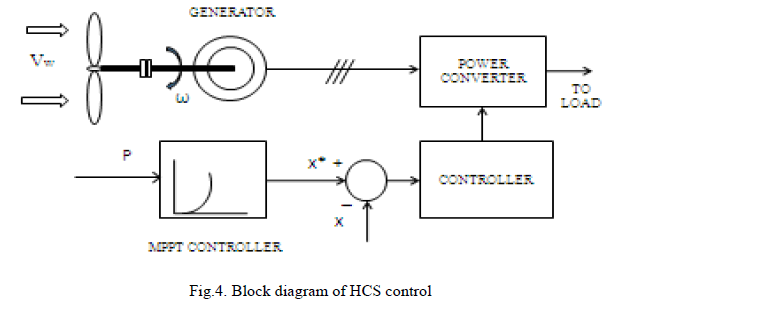image

DOUBLY FED INDUCTION GENERATOR
The studied system here is a variable speed wind generation system based on Doubly Fed Induction Generator (DFIG). The stator of the generator is directly connected to the grid while the rotor is connected through a back-to-back converter which is dimensioned to stand only a fraction of the generator rated power. The DFIG technology allows extracting maximum energy from the wind for low wind speeds by optimizing the turbine speed, while minimizing mechanical stresses on the turbine during gusts of wind.
The optimum turbine speed producing maximum mechanical energy for a given wind speed is proportional to the wind speed. Another advantage of the DFIG technology is the ability for power electronic converters to generate or absorb reactive power, thus eliminating the need for installing capacitor banks as in the case of squirrel-cage induction generator. The AC/DC/AC converter is basically a PWM converter which uses sinusoidal PWM technique to reduce the harmonics present in the wind turbine driven DFIG system. Here Crotor is rotor side converter and Cgrid is grid side converter, Where Vr is the rotor voltage and Vgc is grid side voltage. To control the speed of wind turbine gear boxes or electronic control can be used.

POWER FLOW
The grid connected doubly fed induction generator is the most reliable system to harness the wind power. As the DFIG utilizes the turns ratio of the machine, the converter need not to be rated for machine‘s full rated power. The Rotor Side Converter (RSC) controls the active and reactive power of the machine while the Grid-Side Converter (GSC) maintains the constant DC-link voltage. The GSC‘s reactive power generation is not used as the RSC independently does. But, during the steady state and low voltage periods, the GSC is controlled to take part in reactive power generation. The GSC supplies the reactive current quickly while the RSC results in delays as it passes the current through the machine. These converters can temporarily be overloaded, so that during short circuit periods, the DFIG can make a better contribution to the grid voltage.
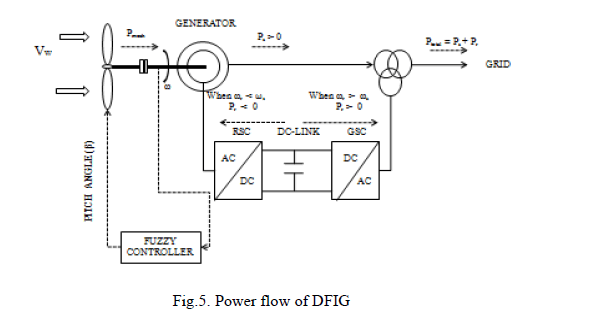image
Power flow of the rotor is bidirectional. When ωr >ωs, the power flows from the rotor to the power grid and when ωr <ωs, the rotor absorbs the energy from the power grid. Power electronic converters between the rotor and grid adjust the frequency and amplitude of the rotor voltage. The control of the rotor voltage allows the system to operate at a variable-speed while still producing constant frequency electricity. The mechanical power and the stator electric power output are computed as follows:
image

PITCH ANGLE CONTROL USING FUZZY LOGIC CONTROLLER
Wind turbine consists of three blades, a servomotor, a controller, rotor rotation sensor, a generator, and some mechanical components. The blades are developed based on NACA (National Advisory Committee for Aeronautics). A Servomotor is used to control the pitch angle of the blade. A rotary encoder is used to measure rotational speed of wind turbine rotor. Fig. 5 shows a diagram block of pitch angle control of wind turbine using a Fuzzy Logic Controller (FLC) for low rated wind speed. The pitch angle of the blade is controlled to maximize the rotational speed of wind turbine and thus the output mechanical power of wind turbine. From Fig.5, a measured rotational speed of wind turbine rotor in rpm from rotary encoder is compared to the desired rotational speed. The FLC processes error, a delta error, and wind speed data of, and v in m/s, respectively. The wind turbine mechanical power (P) is maximized.
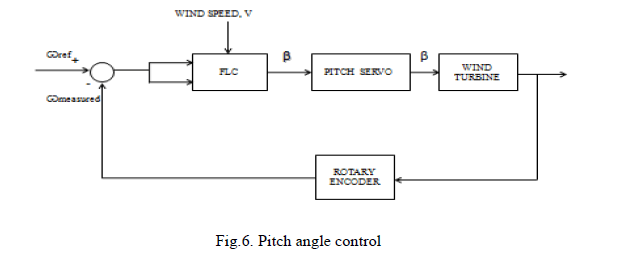image
In other words, to maximize the wind turbine mechanical power, the power coefficient of the wind turbine is optimized via controlling the pitch angle of the blade. Pitch angle (β) is the angle between the direction of wind and the direction perpendicular to the plane of blades. The wind turbine mechanical power (P) can be expressed as
image
Where, ρair - air density
A - area swept by the blades
v - wind speed velocity
CP( λ, β) - coefficient of the wind turbine with the tip speed ratio of λ and blade pitch angle of β.

SIMULATION
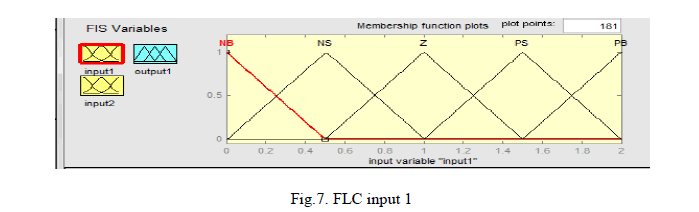
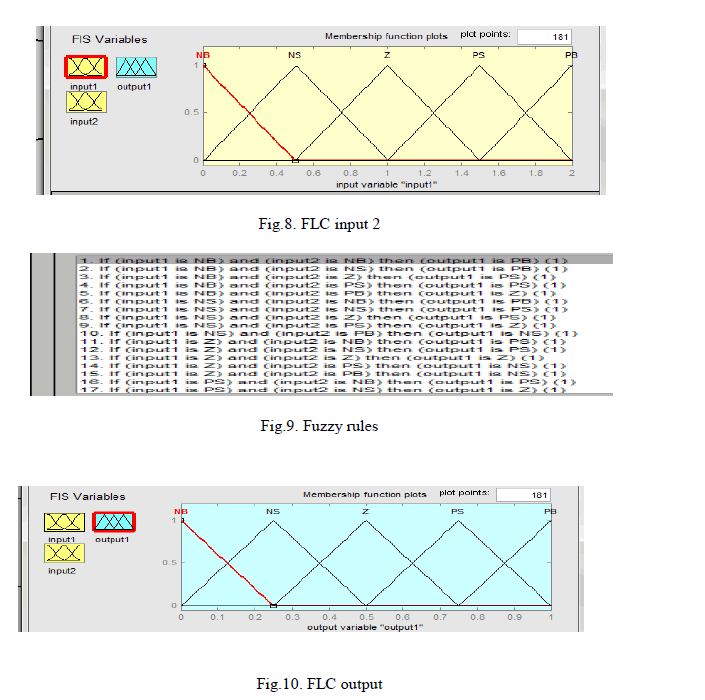
A 9 MW wind farm consist of six 1.5 MW wind turbines is connected to a 25 kV distribution system. The effect of change in wind speed and change in supply frequency are also taken into consideration for the performance analysis of DFIG. The wind turbine with pitch angle fuzzy logic-based control along with the HCS control for variable low rated wind speed is developed and demonstrated. The fuzzy inputs, rules and outputs are shown below. The analysis is also done by changing the demand of reactive power of machine. The performance analysis is done using simulated results obtained from scope, which are found using MATLAB software.
image
image

SIMULATION RESULTS
The generated active power starts increasing smoothly (together with the turbine speed) to reach its rated value. Over that time frame the turbine speed also increases. Initially, the pitch angle of the turbine blades is zero degree. Then the pitch angle is increased from 0 deg in order to limit the mechanical power. We also observed the voltage and the generated reactive power.
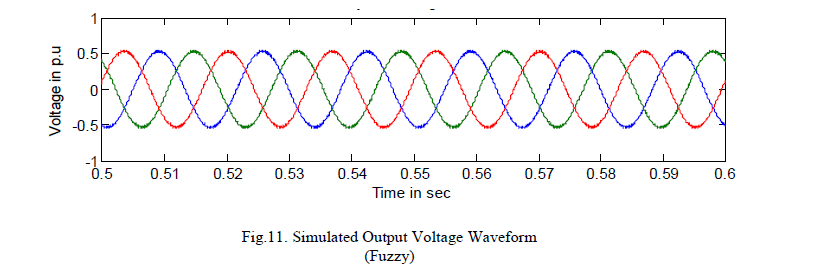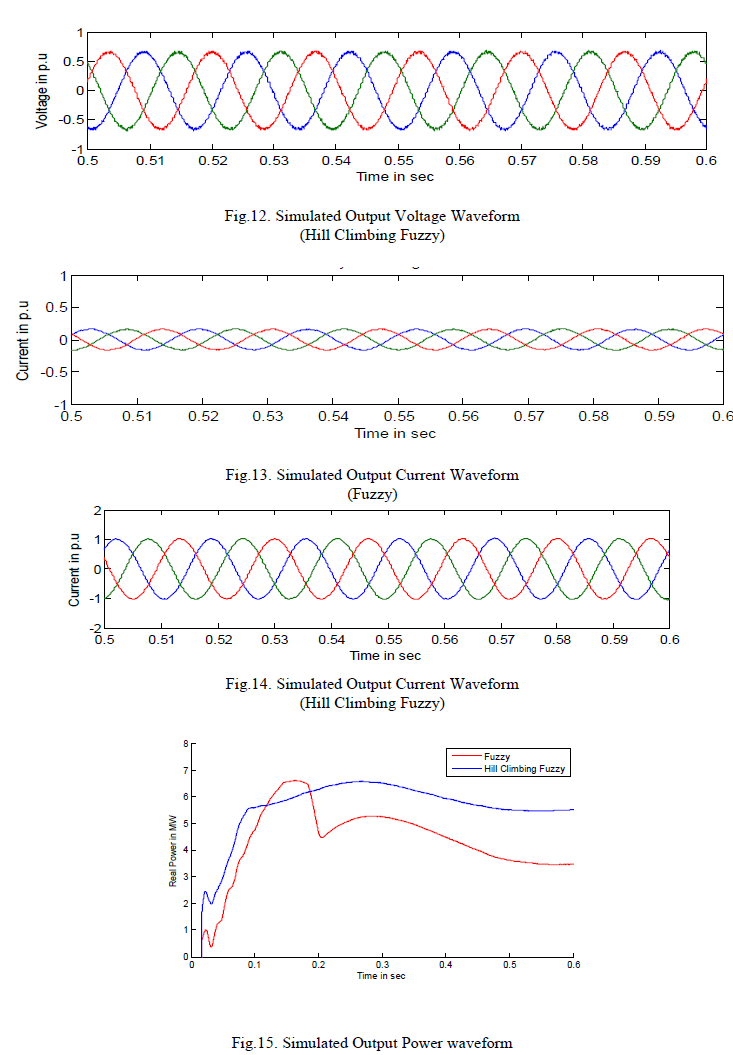image
image
The wind turbine with pitch angle fuzzy logic-based control for variable low rated wind speed has been developed and demonstrated. The use of pitch angle fuzzy logic based control can improve mechanical power response performance of wind turbine compared to the use of a fixed pitch angle or without control.
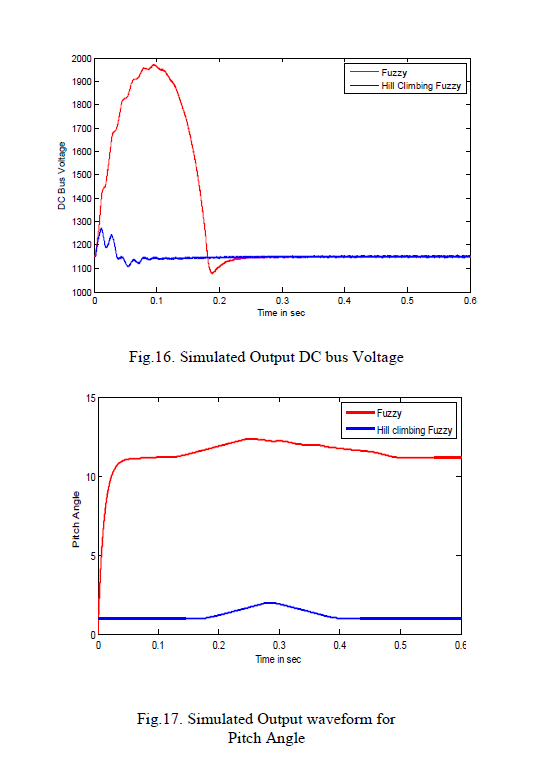image
With the HCS approach, it shows the fine tuning and the values range around 1 degree. The use of pitch angle fuzzy logic based HCS control can improve mechanical power response performance of wind turbine compared to the use of a fixed pitch angle or without control.

CONCLUSION
The mechanical efficiency of a wind turbine depends on the power coefficient. The power coefficient depends on tip speed ratio and pitch angle. Adjustable speed improves the system efficiency as the turbine speed can be adjusted as a function of wind speed to maximize output power. Using DFIG, the adjustable speed can be developed. Pitch angle control is the common method to control the aerodynamic power generated by the wind turbine rotor. Pitch angle control can be implemented by using different controlling variables. Fuzzy logic pitch angle control does not know about the wind turbine dynamics, but is supports when wind turbine contains strong non-linearities. HCS control method is well-suited where wind turbine inertia is very small. It is at this instant, turbine speed reacts to wind speed. The output power is interlinked with turbine‘s mechanical power and rate of change in mechanically stored energy for large inertia wind turbine. This leads to the ineffectiveness of HCS method.

References