Keywords
|
| Image Fusion, Fuzzy Logic, Stationary Wavelet Transform, Fuzzylet Algorithm, Performance Metrics. |
INTRODUCTION
|
| Image fusion is a process of integrating information obtained from various imaging sensors which results in a single image containing complete information. Image fusion is to reduce uncertainty and minimize redundancy in the output by maximizing relevant information from the input images of a scene into a single composite image that is much more clearly informative and is more suitable for visual perception and processing. Image Fusion has got great importance in many applications such as object detection, automatic target recognition, remote sensing, computer vision, flight vision, robotics etc. Image fusion is usually done in three different levels of image representation, they are: |
| i. Pixel level: In this method, integration is performed at a level where pixels are least processed and each pixel in the fused image is calculated from the input images |
| ii. Feature level: It requires extraction of features from the input images first, and fusion is done based on features that matches certain selection criteria |
| iii. Symbol level/Decision level: In this method, output from initial object detection and classification from source image are given as input to fusion algorithm |
| This paper deals with pixel level image fusion. There are various methods for Image Fusion like, image fusion using weighted average, HPF (High Pass Filter), IHS (Intensity Hue Saturation), PCA (Principal Component Analysis, pyramid based decomposition (such as Laplace pyramid decomposition, ratio pyramid, etc.),wavelet transform (WT), etc [1]. Among these, wavelet transform becomes an important aspect of image fusion research with the merits of multi-scale and multi-resolution. In [2], an algorithm of multi-sensor image fusion using wavelets and Principal Component Analysis (PCA) is proposed and comparison of image fusion with different techniques based on fusion quality performance metrics is done. Multi-resolution wavelet transforms provides good localization in both spatial and frequency domains. Discrete Wavelet Transform (DWT) provides directional information in decomposition levels and contains unique information at different resolutions. Wavelets are suffered with shift variant and edges are not produced in the fused image. Stationary Wavelet Transform (SWT) solves this problem which is shift invariant [3]. Since the concept of image fusion is not that certain and crisp, Fuzzy logic is implemented for image fusion in order to incorporate uncertainty to the images [4]. Fuzzy sets are to represent spatial information in images along with their imprecision. By proper tuning of membership functions and by proper formulation of rules, good quality fused image can be obtained using fuzzy logic with less execution time [5] [6]. Fuzzy logic has got application in multi-sensor image fusion also [7].Image fusion using SWT with higher levels of decomposition provides better fusion results. But the fusion rules used in SWT algorithm are very certain and crisp. It is assumed that incorporating fuzzy logic into SWT would give better results by introducing uncertainty to the fusion logic of SWT so that the fusion will preserve more detail spectral and spatial information. |
| This paper proposes a new algorithm for Pixel Level Image Fusion in which fuzzy logic is incorporated into SWT algorithm and hence named as ‘Fuzzylet Fusion Algorithm’, which comprises the advantages of both fuzzy logic and SWT. This algorithm gives better results than using SWT and Fuzzy Logic of similar conditions independently. In this paper all of the three image fusion techniques, SWT, Fuzzy and Fuzzylet are discussed and experiments are done with a set of images. |
IMAGE FUSION ALGORITHMS
|
| A. Stationary Wavelet Transform (SWT) |
| Wavelets are localized waves having finite energy, which are suited for analysis of transient signal. The irregularity and good localization properties make them better basis for analysis of signals with discontinuities. DWT is a type signal representation that can give the frequency content of the signal at a particular instant of time. It provides directional information in decomposition levels and contains unique information at different resolutions. But DWT is shift variant because of down sampling process and if there is a movement of object in the input images, the performance of this method will deteriorate. SWT solve this problem which is translation invariant, without down sampling process. Therefore, all approximation and detail coefficient sub bands have the same size as the input images. The fused image is reconstructed by performing Inverse Stationary Wavelet Transform (ISWT). |
| In the wavelet based image fusion process [2], the steps mainly involved are registering source images, performing wavelet transform on each input images, generating a fusion decision map based on a defined fusion rule and constructing fused wavelet coefficient map from the wavelet coefficients of the input images according to the Fusion decision map. Finally, transform back (ISWT) to the spatial domain. |
 |
| B. Fuzzy Logic |
| Image fusion using fuzzy logic algorithm is known as fuzzy image fusion. The theory of fuzzy sets and fuzzy logic is based on membership functions, usually indicates as μA(x), which describes the degree of membership of element x in fuzzy set A. A Fuzzy Inference System (FIS) is a system that uses fuzzy set theory to map inputs to outputs. The general structure of a FIS used for image fusion is shown in Fig.1. |
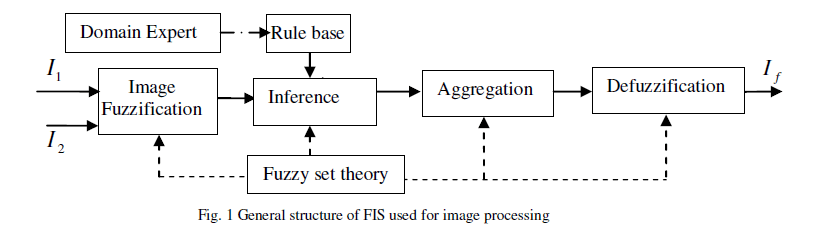 |
| For getting the fused image, the input images must go through the following stages (as shown in Fig. 1): |
| ïÃâ÷ Development of Rule base: Determining a set of fuzzy rules |
| ïÃâ÷ Input Fuzzification: Fuzzifying the inputs using the input membership functions |
| ïÃâ÷ Inference: Combining the fuzzified inputs according to the fuzzy rules to establish a rule strength and finding the consequence of the rule from the rule strength and the output membership functions |
| ïÃâ÷ Aggregation: Combining the consequences to get an output distribution |
| ïÃâ÷ Defuzzification: Defuzzifying the output distribution to get a crisp output |
| In the case of image fusion, the value of each pixel falls under a level of brightness. In this paper the linguistic variables for different membership functions are given according to the pixel value. Algorithm for fuzzy image fusion is given in [5] and [6]. In fuzzy image fusion, selection of membership function and formulation of rules has got great role. FIS toolbox is available in Matlab and can be used for coding as a ‘fis’ file. In this paper ‘Sugeno’ FIS is used, since it takes less execution time than ‘Mamdani’ FIS because the output of Sugeno inference system is a crisp set hence defuzzification is not required for this type. |
| Rule tables for 3 & 5 membership functions are shown in Table I. The linguistic variables for inputs and output membership functions (5 membership functions for each) are taken as Very Low (VL), Low (L), Medium (M), High (H) and Very High (VH) according to the pixel value. For three membership functions, there are only three (L, M and H) linguistic variables. |
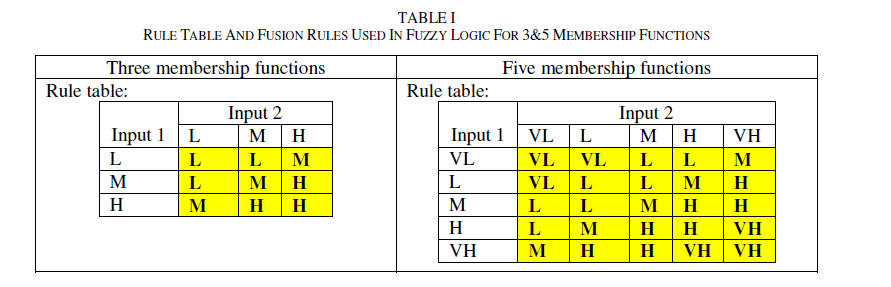 |
| For n number of membership functions, n2 rules are there (ie, for 3 membership functions, 9 rules are there and for 5 membership functions, 25 rules are there). From the rule table, the rules can be formulated using ‘if…..then….’ conditions. For example, consider the first output cell (shaded with yellow) in 3 membership function rule table. For that particular condition, both the inputs are ‘L’ and the output also ‘L’. Hence, the rule can be defined as: |
| If input1 is L and input2 is L then output is L |
| Similarly second rule can be defined as (consider second output cell in 3 membership function rule table): |
| If input1 is L and input2 is M then output is L |
| All other rules can be defined in the same way. |
| The steps involved in fuzzy image fusion algorithm (abbreviated as ( , ) 1 2 F I I ) are: |
| Step 1: Read the images ( 1 2 I &I ) to be fused and convert them into column vector |
| Step 2: Make a fis (Fuzzy) file in Matlab having two input images (in vector form) |
| Step 3: Decide number and type of membership functions for both the input images by tuning the membership functions |
| Step 4: Make rules for input images, which resolve the two antecedents to a single number from 0 to 1 |
| Step 5: Apply fuzzification using the rules developed above on the corresponding pixel values of the input images which gives a fuzzy set represented by a membership function and results in output image in column format |
| Step6: Convert the column form into matrix form to get the fused image f I |
| As the number of membership function increases finer details are taken into consideration. But on the same time, number of rules also increases. So their formulation becomes very difficult. |
| C. FUZZYLET |
| SWT is translation invariant without down sampling process. Fuzzy logic helps in including uncertainties to the fusion logic. To combine the advantages of both fuzzy logic and SWT, fuzzy logic is incorporated into SWT to get a new algorithm and it is named as “Fuzzylet”. It is assumed that Fuzzylet would provide better fusion results than that are obtained by using fuzzy logic and SWT independently. The information flow diagram of image fusion using Fuzzylet is shown in Fig. 2. |
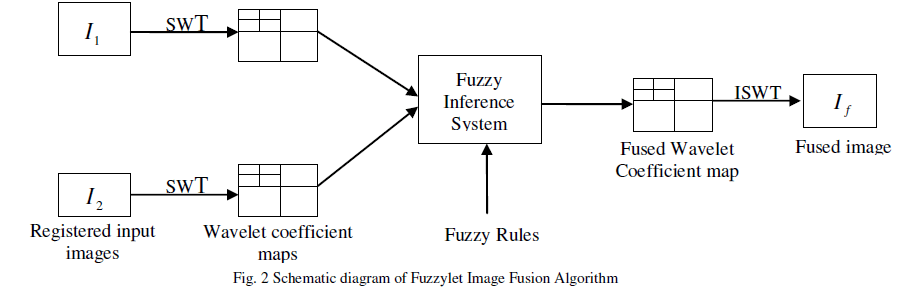 |
 |
PERFORMANCE EVALUATION METRICS
|
| The comparison of the algorithms will be clearer by using fusion quality performance evaluation metrics. The fused images are evaluated by taking the following parameters into consideration. |
| A. Entropy (H) |
| Entropy H is a scalar value representing the entropy of grey scale image. Entropy is a statistical measure of randomness that can be used to characterize the texture of the input image. Entropy is defined as: |
 |
RESULTS AND DISCUSSIONS
|
| Image fusion algorithms (SWT, Fuzzy Logic and Fuzzylet) described in section II are implemented on Matlab and tested on a set of images using numerous fusion quality evaluation metrics (explained in section III). For experimentation, CSIR-NAL indigenously developed SARAS image has been taken as true image r I (reference image) of dimensions 512x512 as shown in Fig. 3. Input (source) images, which are to be fused ( 1 I and 2 I ) are obtained by blurring the true image as shown in Fig. 4. |
 |
| Fused image quality evaluation metrics using SWT based fusion algorithm are shown in Table II. From the table, it is observed that higher level of decomposition in fusion process provides better results at the cost of execution time. The execution time increases as the number of decomposition levels increases. It is also observed that ‘Mean’ metric does not provide any information and hence it may not be useful for evaluating the performance of the fusion algorithm. For this particular dataset, fusion with 4 levels of decomposition provides better results than other levels as shown in Table. Even though level 5 is a higher level, it does not show much difference from Level 4. The best values are indicated as bold. The fused image and error image are shown in Fig. 5. It is observed that the fused image is identical to reference image and error image is almost zero. It shows that SWT with 4 levels of decomposition provides good results. |
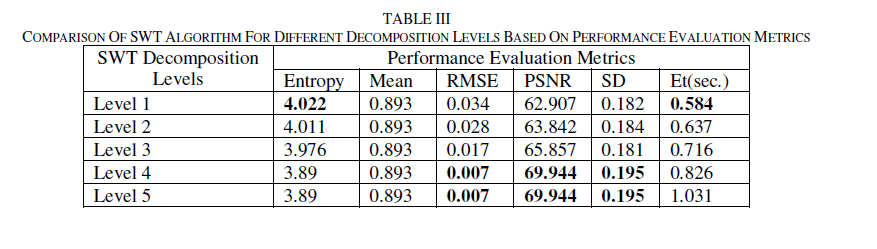 |
 |
| In Fuzzy logic algorithm, the tuning parameters are its membership function and rules. As the number of membership function increases finer details are taken into consideration. But with the increase in number of membership functions, number of rules also increases. For n number of membership functions, n2 rules will be there. So their formulation becomes very difficult. Experiments are done on the source images and fusion quality metrics are analysed with different number of membership functions to find the one which gives better results. Table III gives the performance metrics results for different number of membership functions using Fuzzy logic algorithm. |
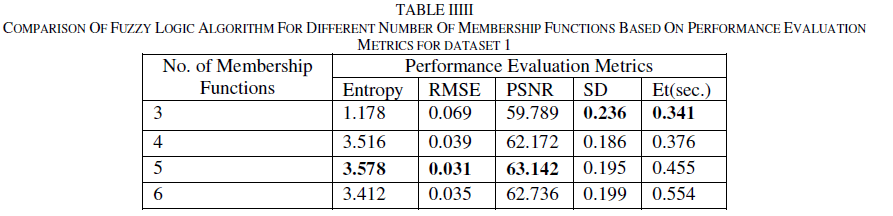 |
| From Table III, it is clear that fuzzy system with 5 membership functions gives best performance. It can be observed that Execution time is lesser for fuzzy logic algorithm compared to SWT (see Table II). Fig. 6 shows the fused and error images using fuzzy algorithm (Sugeno) with 5 membership functions. |
 |
| In Fuzzylet Algorithm, as explained earlier fusion detail coefficients of SWT are obtained from fuzzy logic. So for evaluation, different combinations of fuzzy and SWT are taken. For simplicity only RMSE and PSNR are taken because they are more significant metrics which gives information about how much the fused image resembles reference image. Table IV gives comparison of Fuzzylet algorithm with different combinations of fuzzy membership functions and SWT decomposition levels. |
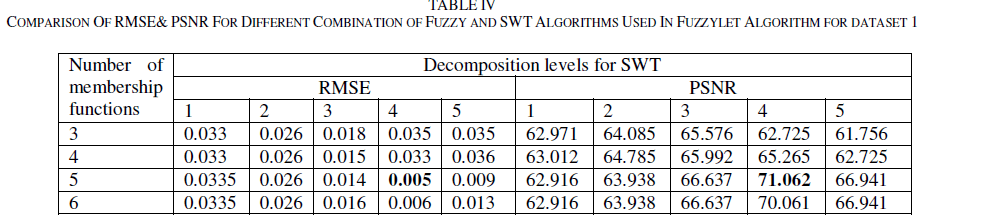 |
| From the Table IV, it is clear that Fuzzylet algorithm gives better results than corresponding Fuzzy and SWT algorithms alone (see Tables II & III). The best results are obtained with 5 fuzzy membership functions and 4 levels of decomposition of SWT with an execution time of 3.32 seconds. And it gives better RMSE and PSNR than the best results with other two methods on cost of execution time. Fused and error images using Fuzzylet algorithm with 5 fuzzy membership functions and 4 SWT decomposition levels are shown in Fig 7. It shows that fused image is identical to reference image and error image is almost zero. |
 |
| Hence from the above discussions, it is clear that Fuzzylet Image Fusion Algorithm gives better results than Fuzzy logic and SWT algorithms at the cost of execution time. |
CONCLUSION
|
| Image fusion algorithms based on SWT and fuzzy logic were developed and demonstrated. It was observed that fusion using SWT with higher levels of decomposition provides better results. Similarly, fuzzy image fusion with more number of membership functions provides better results. SWT based image fusion produces better quality of fused images at the cost of execution time when compared to fuzzy logic based image fusion algorithm. A novel image fusion algorithm (Fuzzylet) had been developed by combining the features of SWT and fuzzy logic. Fuzzylet base image fusion algorithm outperformed compared to SWT and fuzzy based fusion algorithms at the cost of execution time.c |
ACKNOWLEDGMENT
|
| We would like to thank Mr. N Santhakumar, FMCD Department, CSIR-NAL and Prof. K Radhakrishnan, Head of the Department, Electrical & Electronics, M.A College of Engineering, for their constant encouragement and support to carry out this work. |
References
|
- Yanfen Guo, Mingyuan Xie, Ling Yang, “An Adaptive Image Fusion Method Based on Local Statistical Feature of WaveletCoefficients” 978-1-4244-5273-6/9 2009 IEEE.
- VPS Naidu and J.R. Raol, “ Pixel-level Image Fusion using Wavelets and Principal Component Analysis,” in defence journal,vol. 58,No.3, May 2008, pp. 338-352.
- PusitBorwonwatanadelok, WiratRattanapitakandSomkaitUdomhunsakul, “Multi-Focus Image Fusion based on Stationary WaveletTransform and extended Spatial Frequency Measurement”, International Conference on Electronic Computer Technology,2009, pp. 77-81.
- R. Maruthi and K. Sankarasubramanian, “Pixel Level Multifocus Image Fusion Based on Fuzzy Logic Approach”, Asian Journal ofInformation Technology 7(4): 168-171, 2008 ISSN: 1682-3915.
- Harpreet Singh, Jyoti Raj and Gulsheen Kaur, “Image Fusion using Fuzzy Logic and Applications”, Budapest Hungary, 25-29 July. 2004.
- Rahul Ranjan, HarpreetSingh,ThomasMeitzler and Grant R. Gerhart, “Iterative Image Fusion Technique using Fuzzy and Neuro Fuzzylogic and Applications”, Annual Meeting of the North American Fuzzy Information Processing Society,NAFIPS 2005.
- Yi Zheng, Ping Zheng, “Multisensor Image Fusion Using Fuzzy Logic for Surveillance Systems”, 7th International Conference onFuzzy Systems and Knowledge Discovery,2010.
- www.mathworks.in/matlabcentral/fileexchange/authors/104729viewed on 10/10/2013.
|