International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Point Spread Functions of Defocused Optical Systems with Hanning Amplitude Filters

K. Vinod Kumar1, B. Sambaiah2, D. Karuna Sagar3 and R. Sayanna4
  1. Research Scholar, Department of Physics, Osmania University, Hyderabad - 500 007, India
  2. Professor, Department of Physics, Nizam College, (O.U.), Hyderabad - 500 001, India
  3. Professor, Department of Physics, Osmania University, Hyderabad - 500 007, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

The point spread function of defocused optical systems in the presence of primary spherical aberration has been investigated. Significant reduction in the intensity of the central lobe along with the existence of non-zero first minimum results in a severe restriction for Rayleigh criterion to be applied for two-point resolution studies for these systems.

Keywords
PSF, Hanning pupil, Defocusing, Super-resolution.

INTRODUCTION
It is a known phenomenon that the diffraction image of a point object is never a point image. It is a patch of light distributed over a finite region in the image plane. This is known as the Point Spread Function (PSF) of the optical system and is commonly known as Airy pattern when the optical system is purely diffraction-limited. The PSF of an optical system is an important parameter for studying its imaging characteristics. In other words, the performance of an optical system significantly depends on its PSF [1]. The study of imaging properties of optical systems suffering from aberrations from the knowledge of the PSF has become an important method in the design and testing of such systems [2]. In our present study, we have investigated the PSF of a defocused optical imaging system suffering from primary spherical aberration with Hanning amplitude filters.

THEORY
The far-field diffraction characteristics in the case of a circular aperture of an optical system can be derived from its amplitude response or the amplitude PSF. The diffracted light amplitude associated with a rotationally symmetric pupil is given by [3],
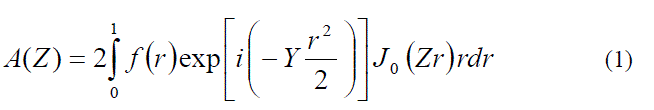image
where f(x) is the pupil function of the optical system; Y is the defocusing parameter in dimensionless coordinates and J0(Zr) is the zero order Bessel function of the first kind; „r‟ is the reduced co-ordinate on the exit-pupil of the system. In the present study, we have considered the Hanning amplitude filters of the first order whose pupil function can be represented by
image
where β is the apodising parameter which controls the non-uniform transmission of the pupil. =0 corresponds to the Airy case. The intensity PSF, B(Z) which is the real measurable quantity can be obtained by taking the squared modulus of A(Z). Thus,
image

RESULTS AND INTERPRETATIONS
Expression (3) has been employed to compute the intensity distribution of the point spread functions of the apodised optical system using twelve point Gaussian quadrature integration methods. Results has been tabulated for apodised aperture with β = 1 and this has been compared with the Airy case (β = 0).
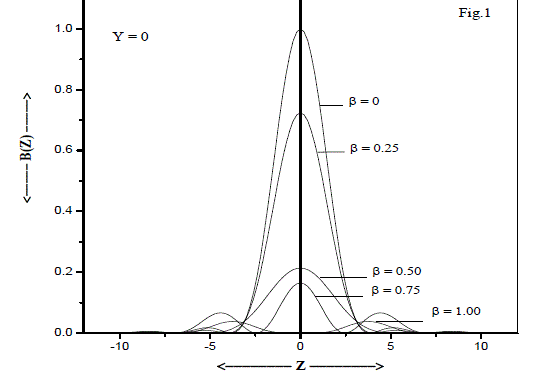image
Fig.1 depicts the intensity distribution curves for the optical system which is at perfectly focused plane (Y = 0). The intensity in the central maximum decreases with the apodisation parameter β. However, for β = 0.5, the optical side lobes are completely suppressed and for β= 1 the diffraction pattern converges towards the centre, thereby rendering the super-resolving nature of the point spread function. The intensity distribution curves for defocused planes Y = π and Y = 2π have been shown in Figs. 2 and 3.
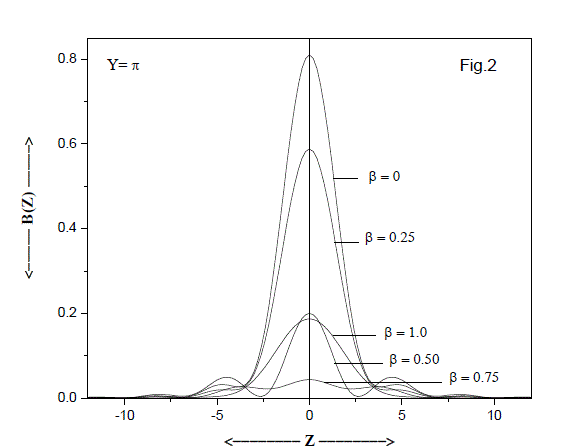image
Table.1 shows the computed values of the positions and respective values of the intensity distribution in terms of central maximum, first minima, first maxima and second minima when there is no apodisation (β = 0). Similarly, Table.2 gives the corresponding tabulated results when the optical system is apodised with β = 1.
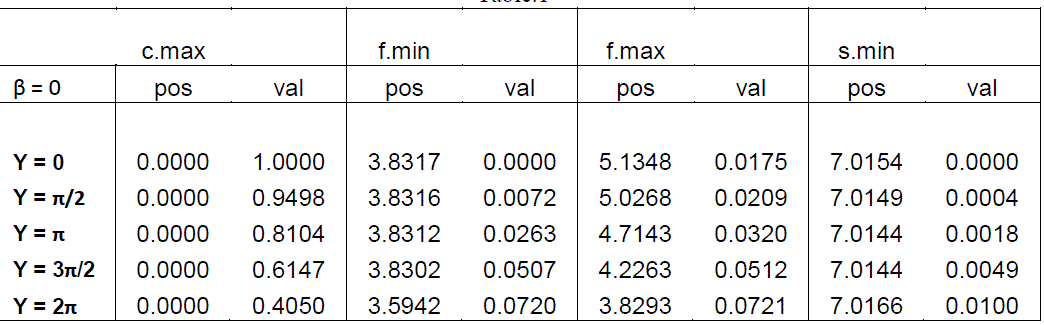image
It can be seen that from both the tables, for Y = 2π the radius of the first dark ring reduces with apodisation. This feature is also found to be seen with defocusing parameter for Airy as well as apodised apertures. Hence the optical systems when apodised with Hanning amplitude filters, there results in the super resolving nature of the point spread functions.

CONCLUSIONS
The process of apodising the optical system with generalized Hanning amplitude filter, suppresses fully or partially the optical side-lobes. For β = 0.5 these side-lobes are totally eliminated for the optical filter considered. The defocusing parameter is effective in shaping the point spread function so that first minima is reduced beyond the Airy case resulting in super-resolving nature of the optical system. Hence, employed Hanning amplitude filters are effective in shaping the point spread function of the given optical systems.

References
  1. K.Surendar, Ph.D. Thesis, Osmania University, Hyderabad, India, 1993.
  2. T.R.Corle and G.S.Kino, “Confocal scanning Optical Microscopy and Related Imaging Systems”, Academic Press, San Diego, 1996.
  3. A.Boiivin, “Theorie et calcul des Figures de Diffraction de Revolution”, Gauthier villars, Paris, 1964.
  4. Jacquint P and Roizen-Dossier B 1964 Progress in Optics ed. E. Wolf (North-Holland Publishing Company, Amsterdam) Vol III, Chapter 2.
  5. Abdul Muhith and D. Karuna Sagar, Defocused point spread functions of two annulus apertures apodised with Hanning amplitude filters, J. P. A. P. Vol.21, No.3, July-Sept., 2009, pp 493-495.