International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Poisson Noise Removal in Biomedical Images using Non-Linear Techniques

Jisha J U1, Sureshkumar V2
  1. PG Scholar, Dept. of Electronics and Instrumentation, Valliammai Engineering college, Chennai, India
  2. Asst.Professor, Dept. of Electronics and Instrumentation, Valliammai Engineering college, Chennai, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Medical images have always been an important factor in diagnosis of disease. Poisson Noise in those images has always been a problem with the image clarity. We propose two technique which combines Multi-Scale Variance Stabilizing Transform (MS-VST), Fast Discrete Curvelet Transform (FDCT) with Thresholding and MS-VST, FDCT with Null Hypothesis testing for effectively removing the Poisson Noise from the medical images. The effectiveness of using these techniques has been analyzed using Peak Signal to Noise Ratio and Universal Image Quality Index.

Keywords
Multi-Scale Variance Stabilizing Transform, Fast Discrete Curvelet Transform, Thresholding, Null Hypothesis, Signal to Noise Ratio,Universal Image Quality Index.

INTRODUCTION
The issues of Poisson Noise occurrence in medical imaging have always been a concern. Poisson Noise occurs in those images due to the arrival of photons to the sensors which are independent of each other. Hence there is uncertainty in the arrival of photons which leads to Poisson Noise. MS-VST [1] stabilizes the variance in Poisson Noise affected images and Gaussianize it to an extent. The advantage of using MS-VST is that it is effective even when the image intensity is very low. It is achieved by pre-processing the input image using a low pass filter. The low pass filter averages out the noise and VST stabilize the variance and Gaussianize it. FDCT [1]-[2] is a second generation curvelet transform which is a multi resolution method. It transforms the input image given to it into FDCT coefficients. It is effective in sparse representation of sharp edges and fine curves [5]. Thresholding is a non-linear technique which is more effective in transform domain. Each transformed coefficient is thresholded by comparing it with a threshold value. Hence the noisy coefficients will be shrunk. In Null Hypothesis testing each coefficient is made absolute by comparing it against the Hypothesis value thus removing all the negative coefficients. In first technique, we combine the MS-VST, FDCT with Thresholding techniques and in another technique MS-VST and FDCT are combined with Null Hypothesis which is applied on an image to denoise it. We have analysed the denoised images using two mathematically defined measures viz Peak Signal to Noise Ratio and Universal Image Quality Index [3] for measuring the effectiveness of using the techniques.

MULTI-SCALE VARIANCE STABILIZING TRANSFORM
A Multi-Scale Variance Stabilizing Transform (MS-VST) is used for approximately Gaussianizing and stabilizing the variance of a sequence of independent Poisson random variables filtered by a low-pass linear filter. This approach is shown to be fast, very well adapted to extremely low-count situations and easily applicable to any dimensional data. The rationale behind applying a Variance-Stabilizing Transformation is to remove the data-dependence of the noise variance, so that it becomes constant throughout the whole data (pixels). Moreover, if the transformation is also normalizing (i.e. it results in a Gaussian noise distribution), we can estimate the final intensity values with a conventional denoising method designed for additive white Gaussian noise.
The main advantage of using MS-VST is that it can be used for low intensity images by pre-processing the input image using a low pass filter. The low pass filter average out the noise and VST stabilize the variance and Gaussianize it.

FAST DISCRETE CURVELET TRANSFORM
FDCT is a second generation curvelet transform which is a multi-resolution method. There are two separate Discrete Curvelet Transform (DCT) algorithms [4]. The first algorithm is the Unequispaced FFT transform. In this algorithm the curvelet coefficients are calculated by irregularly sampling the Fourier coefficients of an image. The second algorithm is the wrapping transform, which uses a series of translation and a wrap around techniques. The wrapping FDCT is more intuitive and has less computation time. It is implemented as shown in fig.1.
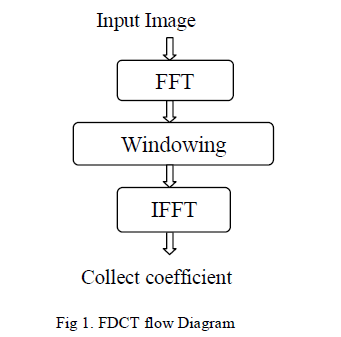image
Firstly, the Fourier sample of the image is obtained by FFT. Then in windowing, the sample is divided into collection of digital corona tiles which is then translated to the origin. Then the parallelogram shaped support of the tile is wrapped around a rectangle centered at the origin. Lastly, Inverse FFT of the wrapped support is determined and finally the resulting curvelet array is added to the collection of curvelet coefficients on which the two non-linear techniques are applied.

THRESHOLDING
It is a simple non-linear technique used for denoising. Each coefficient from the transform domain is thresholded by comparing it with a threshold value. It shrinks coefficients which are above the threshold to an absolute value. It can be expressed as
Coefficient= absolute(coefficient)> Threshold value (1)
We have used soft thresholding which yields more visually pleasant image.

NULL HYPOTHESIS TESTING
Null hypothesis is a technique which is used to nullify the entire noisy coefficient. It is similar to thresholding technique but here the real and imaginary values of coefficients are separately compared with hypothesis value and then replaced in place of original coefficients. It can be expressed as below
Each real value are compared with hypothesis value,
realvalues = absolute(realvalues) > Z (2)
Each imaginary values are compared with hypothesis value.
imagvalues = absolute (imagvalues) > Z (3)
Hypothesis value is calculated by using the formula
Z=(sqrt(10*log10(2*erfcinv(2*1e-3)^2))(coeff of noise free image)
By applying this technique all negative coefficients which are considered as noise will be removed.

MS-VST COMBAINED FDCT WITH THRESHOLDING/NULL HYPOTHESIS
We are using a combination of MS-VST with FDCT to get coefficients in which the non-linear technique is used. The input image is divided into low pass components by using low pass filters. Then the components are given to MSVST where the variance get stabilized and approximately Gaussianize it. Then 2-D DFT is computed with the use of FFT. Then the resulting fourier samples are transformed into curvelet coefficients using windowing technique. The two non-linear techniques uses these coefficients to process the image further. In Thresholding technique, the noisy coefficients are shrunk into an absolute value. Where, in Null Hypothesis the negative coefficients which are considered as noise are removed from the obtained coefficients. Inverse MS-VST and Inverse FDCT is applied to the output of the Thresholding/Null hypothesis values which gives the denoised image.The flow diagram for the proposed system is shown in fig.2.
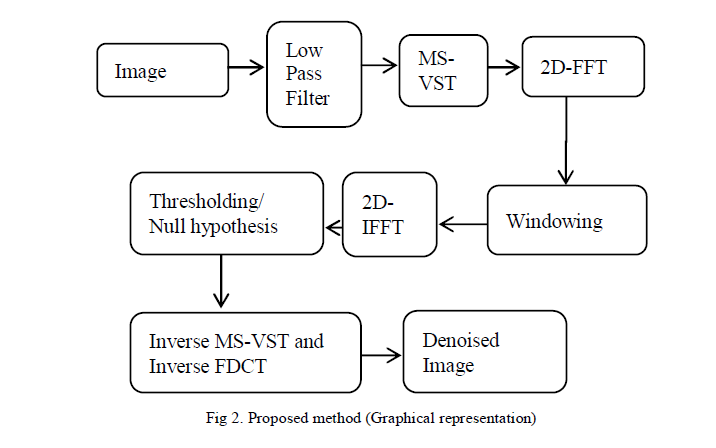image

PERFORMANCE ANALYSIS
To measure the performance of Thresholding and Null Hypothesis testing, Peak Signal to Noise Ratio and Universal Image Quality Index [5] are used. PSNR is the ratio between the maximum possible power of the signal and the power of the corrupting noise. It is widely used as a measure of quality of reconstructed image. PSNR is defined as
image

RESULTS
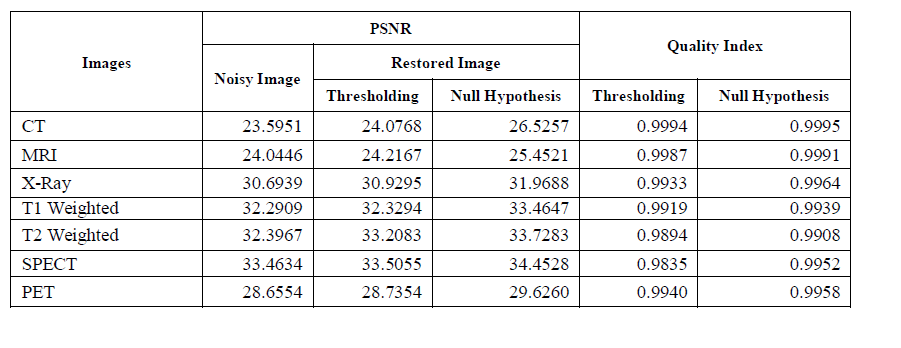
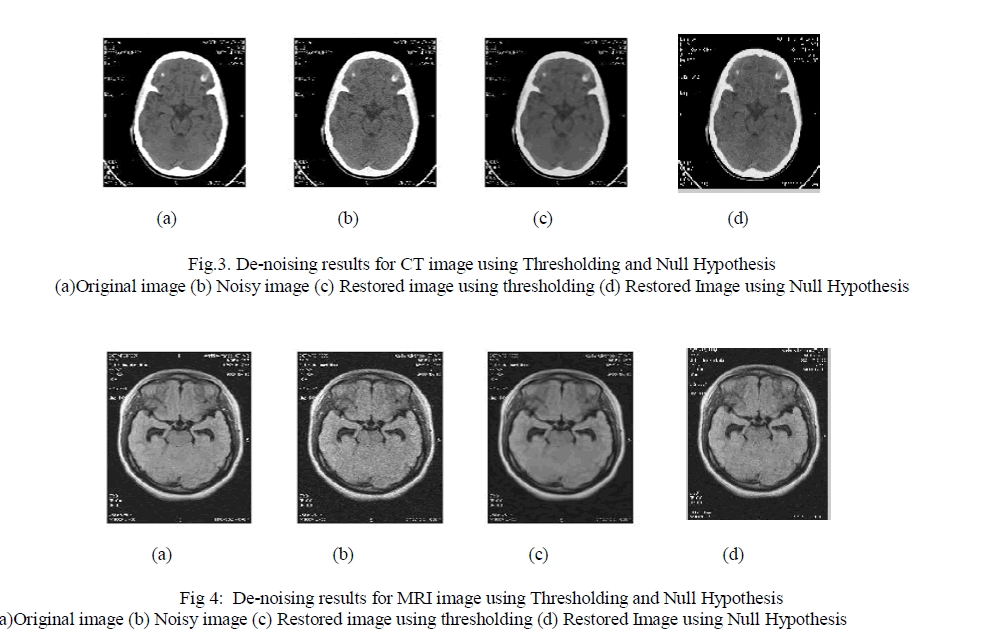
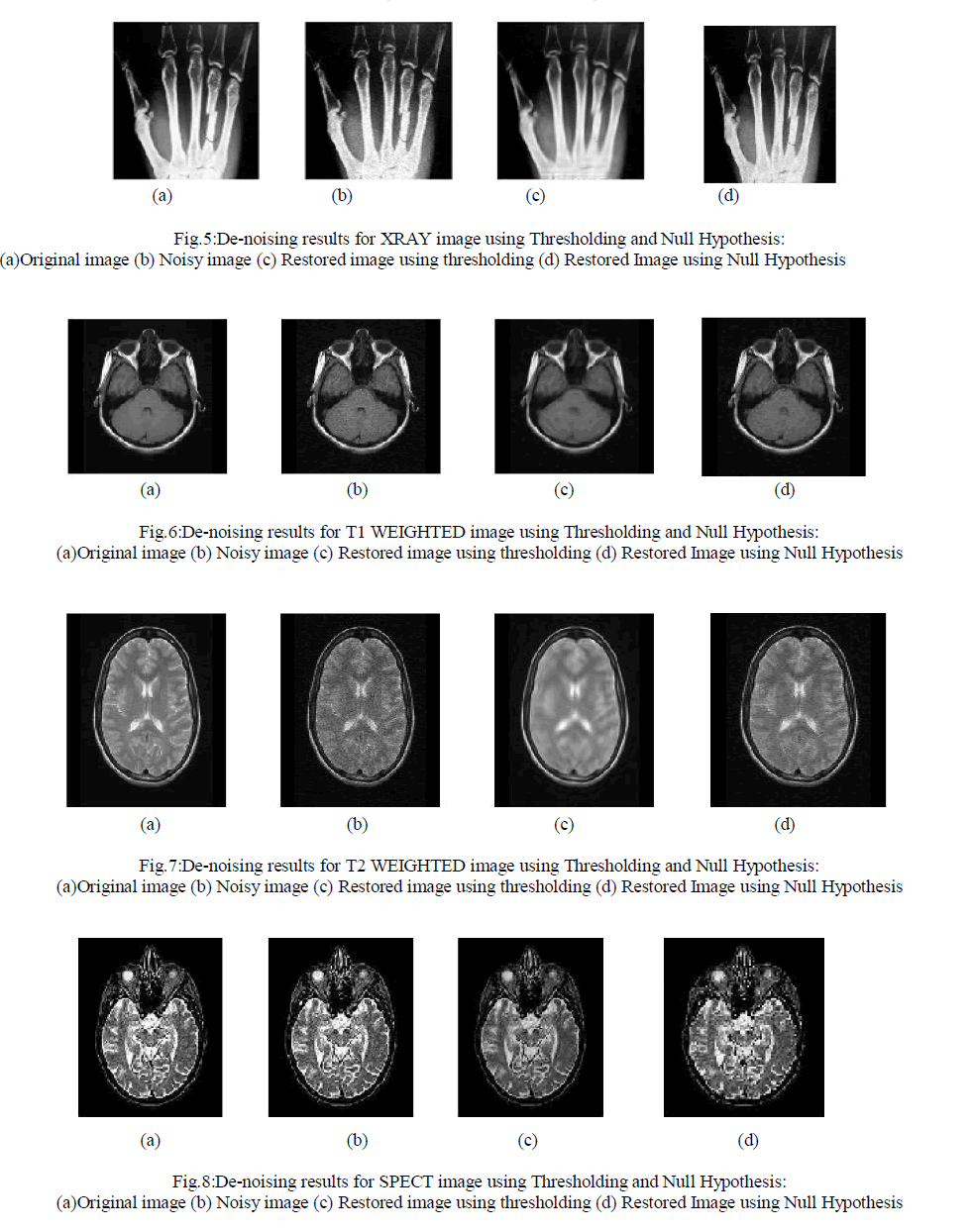
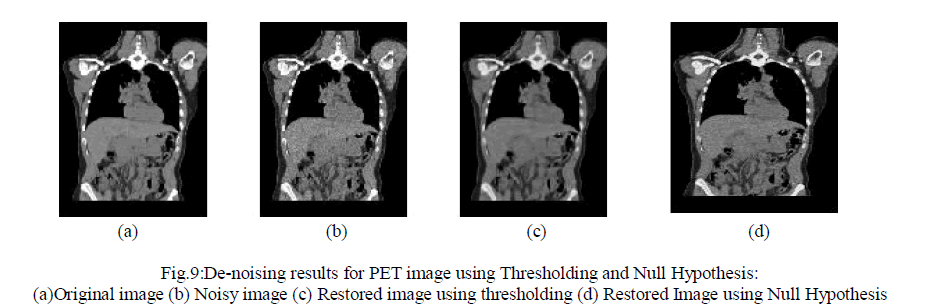
The proposed system is implemented using Matlab 7.6. The performance of the two methods on various medical images was analyzed. PSNR and Universal Image Quality Index were used to evaluate the performance of proposed methods. Both are widely used to measure quality of reconstructed image. The results for CT, MRI, X-Ray, T1 WEIGHTED, T2 WEIGHTED, SPECT and PET images are shown in Fig. 3, Fig. 4, Fig. 5, Fig. 6, Fig.7, Fig.8, and Fig.9 respectively
image
image
image
image

CONCLUSION
We have presented an approach to combine the Multi Scale Variance Stabilizing Transform (MS-VST), Fast Discrete Curvelet Transform (FDCT) with Thresholding and Multi Scale Variance Stabilizing Transform (MS-VST), Fast Discrete Curvelet Transform (FDCT) with Null Hypothesis testing which can be used for Poisson image denoising. From the performance analysis we conclude that the Null Hypothesis yields better denoised image than thresholding method.

References