Power and Area Efficient Implementation
for Parallel FIR Filters Using FFAs and DA

Krishnapriya P.N; Arathy Iyer

Power and Area Efficient Implementation for Parallel FIR Filters Using FFAs and DA

Krishnapriya P.N¹, Arathy Iyer²

M.Tech Student [VLSI & Embedded Systems] , Sree Narayana Gurukulam College of Engineering, Kadayiruppu, Kolenchery, Kerala, India
Asst.Professor, Department of Electronics and Communication, Sree Narayana Gurukulam College of Engineering, Kadayiruppu, Kolenchery, Kerala, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents an algorithm for reducing the hardware complexity of linear phase FIR digital filters. Traditional parallel filter implementations cause linear increase in the hardware cost with respect to the block size. Recently, an efficient parallel FIR filter implementation technique requiring a less-than linear increase in the hardware cost was proposed. This paper makes two contributions. First,the new structure is based on fast FIR algorithm (FFA) that utilizes the symmetry of coefficients; thereby reducing half the number of multipliers in the sub filter section at the expense of increase in adders. Modified FIR filter design using distributed Arithmetic (DA) also provides an approach for multiplier-less implementation of DSP systems. It can completely replace all multiplications and additions by a look up table (LUT) and a shifter-accumulator thereby it can save considerable amount of hardware resources.

Keywords

Digital signal processing (DSP), fast FIR algorithms (FFAs), parallel FIR, symmetric convolution, Look up table (LUT)

I. INTRODUCTION

FIR filters are one of two primary types of digital filters used in digital signal processing (DSP) applications, the other type being IIR.High performance FIR filters have applications in several video processing and digital communications systems. In some applications, the FIR filter circuit must be able to operate at high sample rates, while in other applications, the FIR filter circuit must be a low-power circuit operating at moderate sample rates. The low-power or low-area techniques developed specifically for digital filters can be found in [1, 2, 3, 4, 5, 6, 7].

Traditional FIR filter uses some parallel processing technique to either increase the effective throughput or to reduce the power consumption of the original filter. Parallel processing involves the replication of hardware units. Here the hardware implementation cost is directly proportional to the block size. At the same time if the design area is very limited this technique is not applicable. Therefore, in order to reduce the chip size and to limit the silicon area required to implement the FIR filter it is necessary to realize a new parallel FIR filtering structure that consume less area than traditional parallel FIR filtering structure shown in [1].

In [3], it was shown that complexity of the parallel FIR filters can be reduced by two techniques. In poly phase decomposition small-sized parallel FIR filter structures are derived first and then the larger block-sized ones can be constructed by cascading or by iterating small-sized parallel FIR filtering blocks. Fast FIR algorithms (FFAs) in [10] shows that they can implement an L-parallel filter using approximately (2L − 1) sub filter blocks, each of which is of length N/L. It reduces the required number of multipliers to (2N − N/L) from L × N.

In this paper we provide new parallel FIR filter structures based on FFA consisting of advantageous poly phase decomposition , which can reduce amount of multiplications in the sub filter section by exploiting the inherent nature of the symmetric coefficients, compared to the existing FFA fast parallel FIR filter structure.

This paper is organized as follows. Section II investigates the fast FIR algorithm. In Section III, symmetric convolutionbased new fast parallel FIR filter structures are presented. Section IV presents the design of 27 tap FIR filter. Proposed cascaded FFA filter structures are defined in Section V. Implementation of FIR filter using DA techniques are shown in section VI. In Section VII, simulation results are shown. The comparison of area and power are shown in VIII. Finally, the conclusion is given.

II. FAST FIR ALGORITHM

In many situations parallel processing is avoided due to linear increase in hardware cost.FFA in [10], larger blocksized filtering structures can be constructed through iterations of the small-sized filtering structures.

Consider an N-tap FIR filter can be expressed in time-domain as:

x(n) is an infinite length input sequence and h(n) is the sequence contains the FIR filter coefficients of length N. Consider the poly phase representation of traditional parallel FIR filter,

This block FIR filtering equation shows that the parallel FIR filter can be realized using L2-FIR filters of length N/L. This linear complexity can be reduced using various FFA structures.

A. (2-By-2) Fast FIR Algorithm

Consider the standard 2-parallel filtering structure. From (2), we have

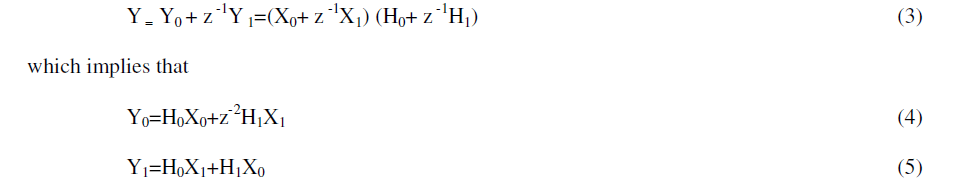Figure 1 shows the resulting 2-parallel FIR filtering structure. This structure requires 2N multipliers and 2(N - 1) additions. Traditional 2-parallel FIR filtering structure requires 5 filtering operations; since Y0 requires 2 and Y1 requires 3 multipliers.

If (5) is written in a different form an equivalent (2-by-2) FFA is obtained:

Y0=H0X0 + z-2H1X1 (6)

Y1=(H0+H1)(X0+X1)-H0X0+H1X1 (7)

The 2 parallel fast FIR filtering structure which results from this (2-by-2) FFA is shown in Figure 2. This structure computes a block of 2 outputs using 3 length N/2 FIR filters and 4 pre/post processing additions. However, the terms X0H0 and X1H1 are found in both Y0 and Y1.These two terms need to be computed only once which means that a total of only 3 filtering operations are required. Therefore, this structure requires 3(N/2) multipliers and 3(N/2-1)+4 adders. 2- parallel fast FIR filtering structure requires about 25% less hardware (area) than the traditional 2-parallel implementation.

B. (3-By-3) Fast FIR Algorithm

The (3-by-3) FFA in [1] is similar to the (2-by 2) FFA from the standpoint that it uses pre/post processing additions to reduce the number of multipliers needed in the implementation. (3-by-3)FFA in [1],[4] produces a parallel filtering structure of block size 3.

Y=Y0+z -1Y1+z -2Y2=(X0+z -1X1+z -2X2)(H0+z-1H1+z-2 H2) (8)

The traditional 3 parallel filtering structure requires 3N multiplications and 3(N - 1) additions. By manipulating (8) through a series of steps, the number of filtering operations can be reduced which in turn reduces the total number of multipliers required to realize the 3-parallel filtering structure. The (3-by-3) FFA in fig 3 is obtained by several applications of the same technique that was used to produce the (2-by-2) FFA.This structure requires 6 length- N/3 FIR filters and 10 pre/post-processing additions to realize the proper transfer function. The (3-by-3) FFA structure requires 6(N/3) multipliers and 6(N/3-1) +10 adders.

III. SYMMETRIC CONVOLUTION BASED FFA

Symmetry of coefficients can be utilized by poly phase decomposition to earn as many sub filter block as possible which contain symmetric coefficients. Half the number of multiplications in the single sub filter block can be reused for the multiplications of whole taps. For an N-tap L parallel FIR filter the total amount of saved multipliers is (N/2L).

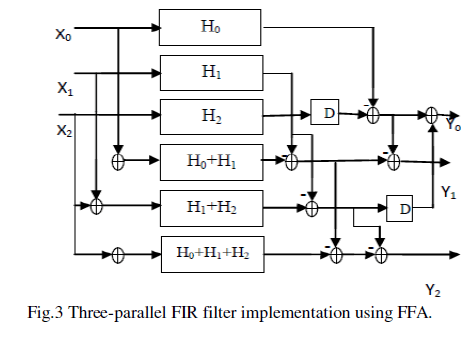
A. Symmetric Convolution Based 3 Parallel FFA

The same technique used in (5) is applied 4 times in order to derive the 3 parallel FFA. Fig. 4 shows implementation of the proposed three-parallel .It shows that when (N mod 3= 0) ie, for or a set of symmetric coefficients in odd length N. It can earn two more sub filter blocks containing symmetric coefficients.

IV. 27 TAP FIR FILTER DESIGN

Our aim is to design an area efficient 27-tap FIR filter .It consist of a set of symmetric coefficients : {h(0), h(1), h(2),h(3), h(4), h(5),h(6), h(7), h(8), h(9),………………………………………h(26)}

Where

h(0)=h(26), h(1)=h(25), h(2)=h(24), h(3)=h(23), h(4)= h(22), h(5) = h(21), . . . , h(12) = h(14),

While designing a 27 tap 3-parallel FIR filter structure :

Step 1: Find out the filter coefficients from Matlab.(Using Remez Exchange Algorithm)

Coefficient calculation is done in Matlab using Remez Exchange Algorithm. firpm designs a linear-phase FIR filter using the Parks-McClellan algorithm . The Parks-McClellan algorithm uses the Remez exchange algorithm and Chebyshev approximation theory to design filters with an optimal fit between the desired and actual frequency responses. Filter coefficients obtained from Matlab is shown in Table I.

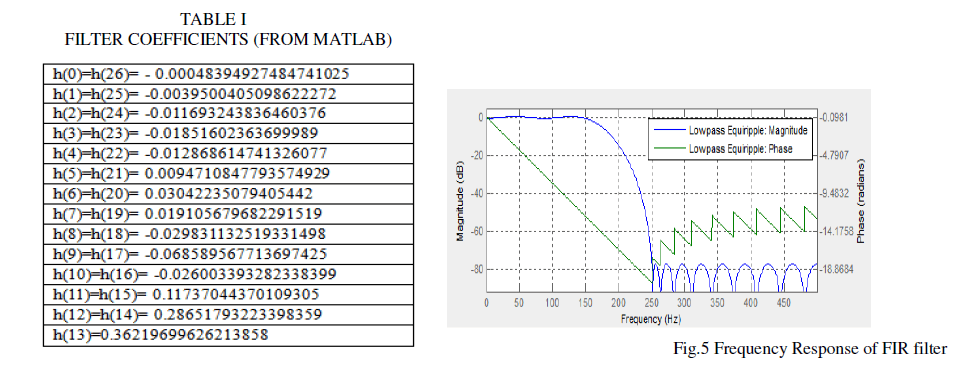Figure 5 shows the frequency response of an FIR filter. FIR filters can easily be designed to have a linear phase characteristic. Linear phase can be obtained in four ways, combinations of even or odd symmetry with even or odd length.

h (N-1-k) = h (k), even symmetry} for 0< k <N

h (N-1-k) = -h (k), odd symmetry } for 0<k<N

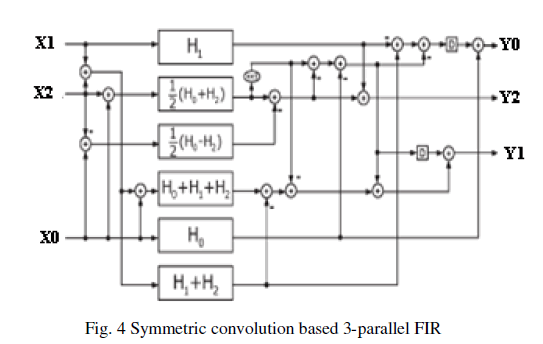
Step 2: Partition these filter coefficients in to 6 sub filter blocks.

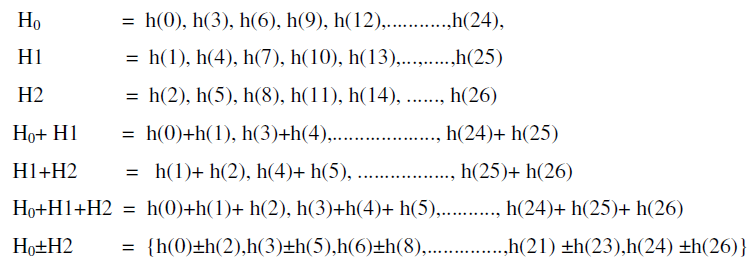Step 3: Check whether existing any symmetry in between the sub filter blocks.

Proposed three-parallel FIR filter structure is shown in figure 4. It enables four (H1,H0±H2,H0+H1+H2,H1+H2) sub filter blocks with symmetric coefficients in total , whereas the existing FFA parallel FIR filter structure has only two ones out of six sub filter blocks.

V. CASCADED FFA

In many design situations, it is necessary to use a parallel FIR filter with greater level of parallelism. When cascading the proposed FFA parallel FIR structures for larger parallel block factor the increase of adders can become larger. Therefore other than applying the proposed FIR filter structures to all the decomposed sub filter blocks ,the existing FFA structure which have more compact operations in pre and post processing blocks are employed for those sub filter blocks that contain no symmetric coefficients [2]-[12].

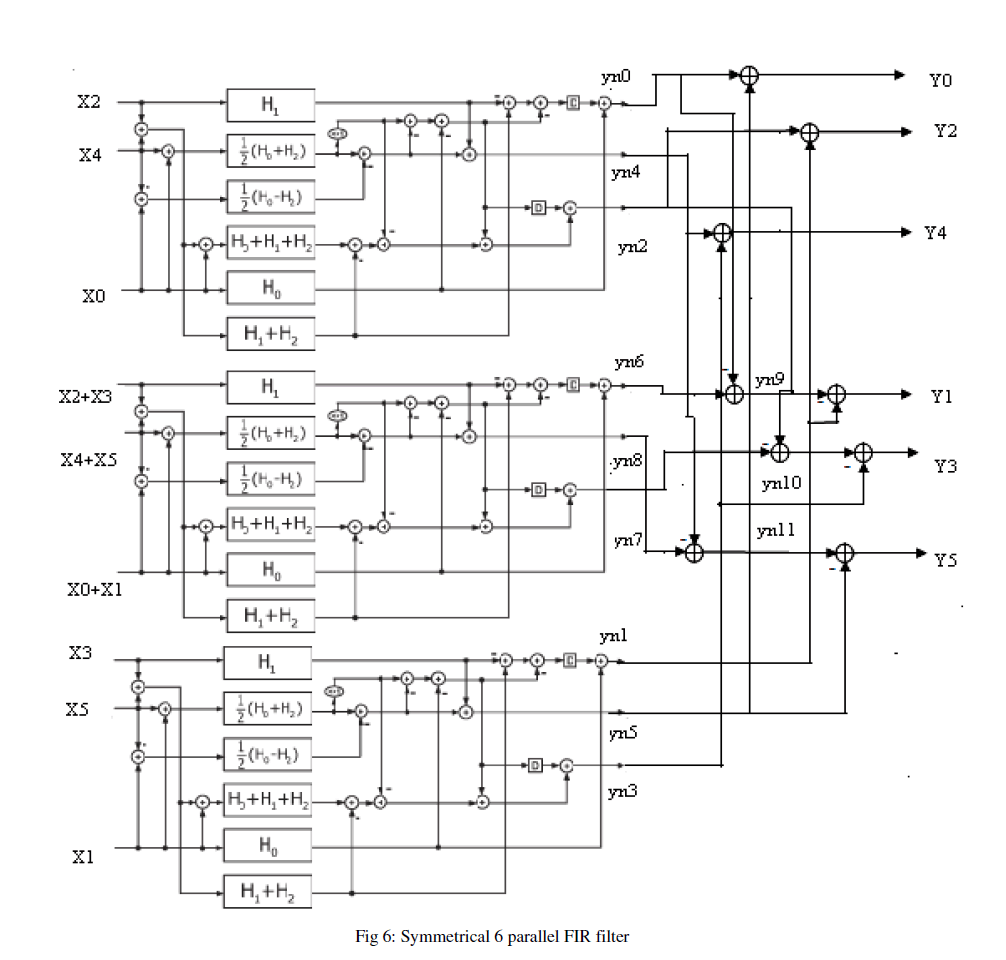For example the 6 parallel FIR filter shown in fig. 6 is generated by cascading a (2-by-2) FFA with a (3-by-3) FFA. The (2-by-2) FFA is applied resulting in 3 filtering operations. The (3-by-3) FFA is then applied to each of these filters producing the 18 filtering operations that are required in the 6-parallel filtering structure. When (2-by-2) and (3-by-3) FFAs are cascaded, the (2-by-2) FFA is always applied first as this will lead to the lowest implementation cost. The resulting 6 parallel filtering structure requires18N/6, 3N, multipliers and 42+18(N/6-1) adders.

VI. DIGITAL FIR FILTER IMPLEMENTATION USING DA TECHNIQUE

Distributed Arithmetic (DA) provides an approach for multiplier-less implementation of DSP systems. It replaces all multiplications and additions by an LUT and a shifter-accumulator. It can save considerable hardware resources through using LUT. DA in figure 7 can be used to compute sum of products.

The filter coefficients are already known, therefore multiplication of each of the filter coefficients by the input sequence becomes a constant. These partial products are recomputed and stored in a look up table. According to the LSB of input sequence, we can conserve the coefficient values in LUT unit shown in table III.

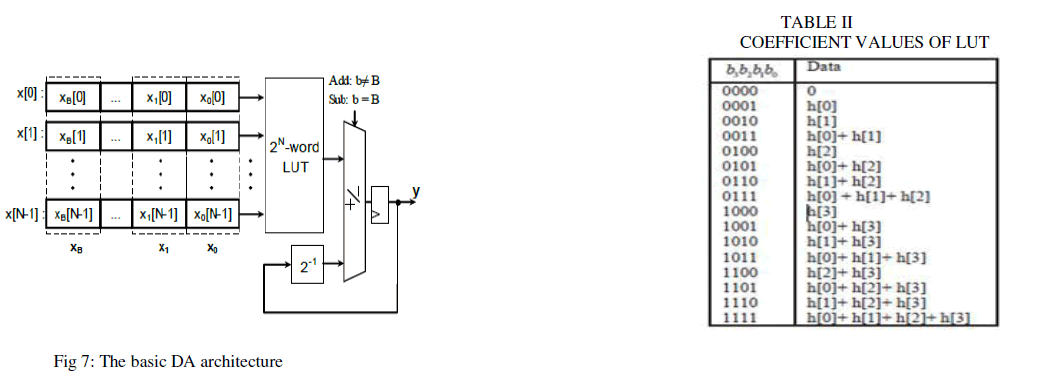With the increase of filter order, the scale of LUT will increase dramatically which will cost more time to look table and more memory to store the values. Therefore, we can divide the LUT unit into small LUT units in figure 8 to solve this problem. Then the values of the divided LUT units are added as the final value.

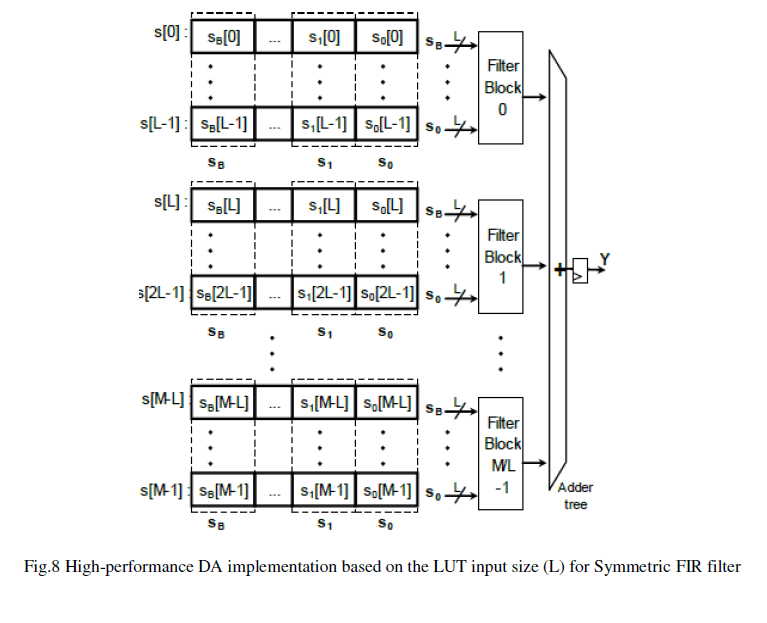VII. SIMULATION RESULTS

Simulation of 27 tap 3 parallel and 6 parallel FIR filter is carried out in Modelsim altera 10.1b. Xilinx ISE 13.3 is used for designing the FIR filter that uses both DA and FFA algorithm and are implemented in VIRTEX 5 FPGA. Simulation results shows that FIR filter designed using DA consumes less power can save considerable hardware resources through using LUT to take the place of MAC units and less area as compare to the proposed 3 parallel filter implementation.

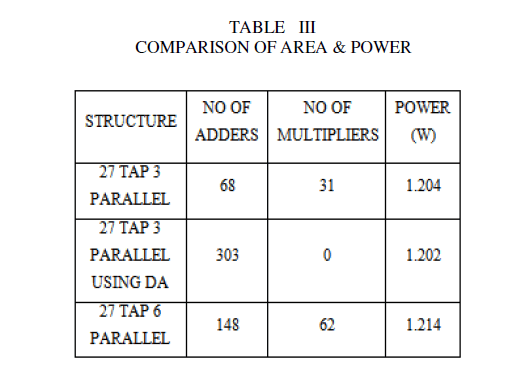Compared to the existing 3 parallel FIR filter structure, proposed structure enables reduced amount of multipliers at the expense of increase in adders. By using distributed arithmetic, we can completely replace all multipliers by using 303 adders. In 27 tap 6 parallel FIR filter, the device utilization is more compared to the 3 parallel FIR filter.

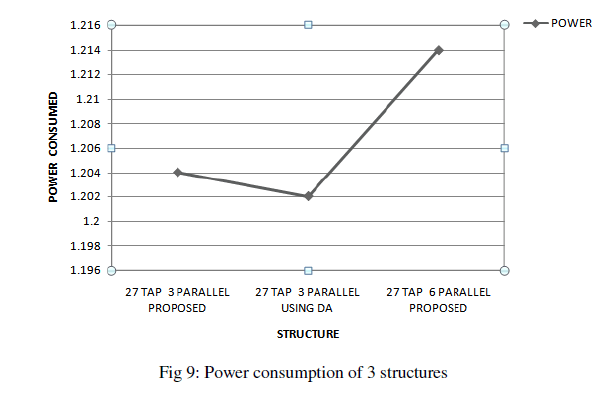Figure 9 shows the power analysis of different structures. Compared to the proposed 3 parallel filter implementation, structures based on distributed arithmetic consumes less power and can save considerable hardware resources.

VIII. CONCLUSION

This paper presents the design and implementation of 27 tap 3 parallel & 6 parallel linear phase FIR filters. Multipliers are the major portions in the hardware consumption for an FIR filter .The new structure exploits the symmetry of coefficients and saves a significant amount of multipliers at the expense of additional adders. A multiplier less FIR filter is also implemented by using distributed arithmetic technique. Simulation results shows that FIR filter design using DA consumes less power and area as compared to the proposed 3 parallel filter implementation.

ACKNOWLEDGMENT

Krishnapriya P N would like to thank Ms. Arathy Iyer Assistant professor ECE Department who had been guiding throughout the project and supporting me in giving technical ideas and motivating me to complete the work efficiently and successfully.

References

Area-Efficient VLSI Implementation for Parallel Linear-Phase FIR Digital Filters of Odd Length Based on Fast FIR Algorithm. IEEE transactions on circuits and systems—ii: express briefs, vol. 59, no. 6, June 2012
Yu-Chi Tsao and Ken Choi, Senior Member, IEEEA. Parker and K. K. Parhi, “Low-area/power parallel FIR digital filter implementations,” J. VLSI Signal Process. Syst., vol. 17, no. 1, pp. 75–92, Sep. 1997
J. G. Chung and K. K. Parhi, “Frequency-spectrum-based low-area low power parallel FIR filter design,” EURASIP J. Appl. Signal Process., vol. 2002, no. 9, pp. 444–453, Jan. 2002.
K.K. Parhi, VLSI Digital Signal Processing systems:Design and Implementation. New York: Wiley, 1999.
Z.-J. Mou and P. Duhamel, “Short-length FIR filters and their use in fast nonrecursive filtering,” IEEE Trans. Signal Process., vol. 39, no. 6, pp. 1322–1332, Jun. 1991.
J.I. Acha, “Computational structures for fast implementation of L-path and L-block digital filters,” IEEE Trans. Circuits Syst., vol. 36, no. 6, pp. 805–812, Jun. 1989.
C. Cheng and K. K. Parhi, “Hardware efficient fast parallel FIR filter structures based on iterated short convolution,” IEEE Trans. Circuits Syst.I, Reg. Papers, vol. 51, no. 8, pp. 1492–1500, Aug. 2004.
C. Cheng and K. K. Parhi, “Furthur complexity reduction of parallel FIR filters,” in Proc. IEEE ISCAS, May 2005, vol. 2, pp. 1835–1838.
C. Cheng and K. K. Parhi, “Low-cost parallel FIR structures with 2- stage parallelism,” IEEETrans.Circuits Syst. I, Reg. Papers, vol. 54,no.2, pp. 280–290, Feb. 2007.
Y.-C. Tsao and K. Choi, “Area-efficient parallel FIR digital filter structures for symmetric convolutions based on fast FIR algorithm,” IEEE Trans Very Large Scale Integr. (VLSI) Syst., vol. 20, no. 2, pp. 366–371,Feb. 2010.