Research & Reviews: Journal of Pure and Applied Physics
MenuISSN: 2320-2459
ISSN: 2320-2459
1Department of Physics, Govt. College for Women, M.A. Road Srinagar, 190 001, India
2Department of Physics, University of Kashmir, Srinagar 190006, India
Received Date: 08/08/2017; Accepted Date: 02/03/2018; Published Date: 12/03/2018
Visit for more related articles at Research & Reviews: Journal of Pure and Applied Physics
The neutrino cross-sections on nucleons and nuclei across all energy scales from eV to GeV and beyond are very small and the uncertainties influx is also large. Moreover, there are many processes which contribute simultaneously to neutrino interaction cross-sections. This makes the analysis of data and theoretical predictions more challenging. Yet it is crucially important to know the cross-sections as an essential input to the growing pursuit of neutrino oscillations and the kind of signals i.e., the final states observed. This study covers the results for neutrino interactions from MeV to GeV scales of energy by using mono-energetic, single favour neutrino beams with different targets at different stages of analysis with an emphasis on experimental findings. In the present contribution, we have used NuWro, a new neutrino Monte Carlo generator, to generate events and compute the cross-sections for neutrino-nucleus interactions.
Cross-section, Pion production, Neutrino-nucleus interactions, Neutrino oscillations, Neutrino mass, Mixing
Advancing our understanding of neutrino oscillation parameters requires building a more complete picture of neutrino interactions. This poses a series of important theoretical and experimental challenges. In this context neutrino event generators are an interface between theory and experiment and these play a vital role in the study of neutrino interactions from conception of an experiment to the final physics publication. Some of the important neutrino event generators based on Monte Carlo simulations are NuWro [1]. The purpose of the event generators is to evaluate the feasibility of some proposed experiment by way of optimizing the detector design, analyzing the collected data samples and evaluating systematic errors and therefore assessing its physics reach. The use of simulations allows us to examine more complex systems than we otherwise can do. As for example, it may look fairly simple to solving the equations which describe the interactions between two atoms but for hundreds or thousands of atoms, it is not so easy to solve the same equations. With simulations, a large system can be sampled in a number of random configurations and that data can be used to describe the system as a whole. This makes the neutrino event generators impressively polymorphic tools.
The present study has been carried out with NuWro [1] which is a relatively new Monte Carlo generator. It handles all important processes in neutrino-nucleus interactions as well as the hadronization due to deep inelastic scattering (DIS) and intra nuclear cascade. It is simple, elaborate and light weight but full featured and serves as a tool to assess the relevance of various theoretical models being investigated currently [2]. NuWro is organized around the event structure which contains three vectors of particles viz; incoming, temporary and outgoing. It also contains a structure with all the parameters used and a set of boolean ags tagging the event as quasi-elastic (QE), resonance excited scattering (RES), deep inelastic scattering (DIS), charged current (CC), neutral current (NC) etc. The input parameters are read at start-up from a text le and the events are stored in the ROOT tree le to simplify further analysis. The main motivation of the authors of NuWro was to have tools to investigate the impact of nuclear e ects on directly observable quantities with all the final state interactions included. Now, NuWro simulates all the essential interactions and it is possible to be used in the experiments. As for instance, it has been included in the ICARUS experiment [3] with the task of improving NUX+FLUKA code in the single pion production region.
The basic algorithms of NuWro follow the other known codes such as NEUT, NUANCE, NEUGEN/GENIE etc. In order to facilitate comparisons, NuWro allows running simulations choosing easily the values of parameters, sets of form factors, models of nucleus etc. T he important features of NuWro are: ne hadronization model [4], description of resonance region without Rein-Sehgal approach [5] and implementation of spectral function as an improvement with respect to Fermi gas model [6]. NuWro is a generator of interactions only. The neutrino is selected according to information about the beam and the target is selected as (nucleus or free nucleon). This is followed by choosing a model of nucleus such as (Fermi gas, local density approximation, effective potential, spectral function) and the inter nuclear cascade is switched on. Like most of the neutrino event generators NuWro is based on impulse approximation scheme according to which a primary neutrino interaction occurs on one of the quasi-free nucleons of the target nucleus followed by final state interactions (FSI) due to propagation of the hadrons through nucleus before these are detected. The NuWro FSI code has recently been incorporated with the Oset model [7] which selects the neutrino interaction point inside the nucleus according to the nuclear matter density.
Neutrino cross-sections are an important component in all neutrino experiments. Interest in the study of neutrino scattering has increased due to the need of such information in the interpretation of neutrino oscillation data. For both charged current (CC) and neutral current (NC) interaction channels, neutrino scattering results have been collected over many decades for a variety of targets and analysis techniques and also for the different detector technologies. New and intense accelerator based neutrino experiments such as No A [8], MINOS, Mini BOONE etc., have been set up for neutrino oscillation investigations. These experiments are re-measuring the neutrino cross-sections with incorporation of nuclear effects and of improved neutrino flux calculations. The conventional neutrino scattering measurements have provided an insight into nucleon structure and the Standard Model. While-as electron scattering measurements have uncovered many mysteries of nuclear structure, but not all of those mysteries have been solved. Neutrinos, because these sample the quarks and the nucleons in a nucleus differently from charged leptons, can provide new insight into the nuclear environment. Moreover, the neutrino experiments require having very intense, well understood beams and ne-grained detectors in order to minimize the statistical and systematic errors. Though the previous experiments from the bubble chamber era (70s-80s) have measured neutrino interactions with precision detection techniques but these were limited by low statistics and large flux uncertainties. In the 80s and 90s, neutrino scattering measurements moved to higher energies to probe nucleon structure and get higher statistics but in the recent past, the neutrino oscillation measurements have pushed the beam energies lower, into regions of interest in oscillation space such as at T2K [9]. There is also a need for these neutrino oscillation experiments to determine more precisely the signal and the background rates in their detectors which has precipitated a resurged interest for neutrino interactions in the first few GeV energy range. Such measurements had not been updated for decades, having first been measured in bubble and spark chamber experiments. Therefore more and more such measurements are sorely needed for present and future neutrino oscillation experiments operating in this energy range.
Additionally, the elusive nature of neutrinos and the inherent difficulty in their detection has created many false signals. The detection of neutrino is inferred indirectly by the particles produced in the process, if at all it undergoes any interaction. As an example, if a vμ scatters quasi-elastically off a neutron, we are left with a charged muon and proton
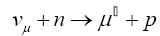
This implies that we need to build low mas detectors with extremely ne tracking capability. However, due to the extremely small size of neutrino cross-sections, the actually constructed detectors have large size and high mass to have enough event rates to perform useful studies.
The measurement of neutrino-nucleus interaction cross-sections is a relatively new area of study which aims at understanding the bare interactions of neutrinos with protons and neutrons through simpler targets like Hydrogen and Deuterium. However, since the oscillation experiments such as NovA [10]. Firely on kton-scale far detectors, these have to use heavier targets such as carbon, iron, heavy water or argon. At the heart of many of the aforesaid experiments, is the need for neutrinos to interact with other standard model particles. Thus accurate predictions for neutrino-nucleus cross-sections are needed in the analyses of on-going and future experimental studies of neutrino reactions at intermediate energies, that is, the energies beyond the nuclear resonance region. The energy spectrum of naturally produced neutrinos starts from fractions of electron volts and spans an impressive range. The large variety of relevant neutrino energies and the tendency to study neutrino-nucleus interactions at increasing energies call for the use of relativistic kinematics and quite naturally also for relativistic models such as the relativistic fermi gas (RFG) model [11] of non-interacting nucleons, very often incorporated as the standard tool in monte carlo neutrino event generators for accelerator and astro particle neutrino experiments. The usual approximation used to compute neutrino-nucleus cross-sections from theoretical models, namely Impulse Approximation Scheme [12] has been proved reliable to predict neutrinonucleus scattering. The final state interactions (FSI) imply to have a sizeable effect on the cross-sections for neutrino energies of several thousand MeVs. FSI are however absent for RFG calculations and thus it comes as no surprise the need of ne-tuning parameters of the RFG models in order to reproduce the experimental data. Therefore, improved calculations of such final state interactions (FSI) have been undertaken by a number of groups [13].
Measurement of Neutrino Interaction Cross-Sections
Generally cross-section refers to a slice or an area of an object but the subatomic particles are so small that aiming individual particles at each other is out of the question. The best anyone can do is to shoot a lot of them in the same general area. For instance, when particle physicists measure the proton-proton to top-antitop cross-section, they are counting how many top-antitop pairs were created when a given number of protons were red at each other. For neutrinos, the problem is even worse; because these did not interact with the other particles in the Universe even only after one second of the Big Bang [14]. This is because these had even less energy-per-particle than the photons do, as electron/positron pairs are still around at that time. Neutrinos interact only by the weak force: hence the reaction cross-sections are much smaller than those of other particle species. For electron-neutrinos the elastic scattering with electrons can be mediated by charged and neutral weak bosons (W and Z), whereas the scattering of muon and tau neutrinos from electrons is mediated only by the neutral boson. Hence the total cross-sections are different.
To perform any of the measurements with neutrinos, we need to be able to produce them artificially. Conventional neutrino beams are made in much the same way as neutrinos from cosmic ray interactions. A proton synchrotron delivers bunches of high energy protons onto a fixed target creating a beam of pions and kaons. Pions decay to muons and muon-neutrinos with a branching ratio of 100% [15]. Similarly the kaons decay to muons and muon-neutrinos with a branching fraction of 63%.
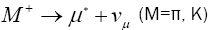
A complication is that muons can also decay to generate electron-neutrinos which one may not want in a pure beam.
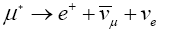
Therefore, at the end of the decay tunnel is a long shield designed to absorb mesons which haven't decayed, to stop the charged muons in the beam, letting only the neutrinos through.
The neutrino energy spectrum can be determined from the kinematics of the two-body decay of the meson. The energy E of the neutrino at an angle in the laboratory frame can be related to the same quantities in the meson rest frame by
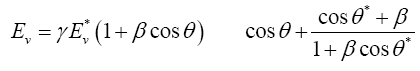(1)
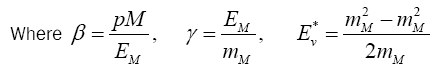(2)
The minimum and maximum neutrino energies come from the cases where the neutrino is emitted forwards and backwards, respectively in the pion rest frame. That is when cosθ*=±1. In this case
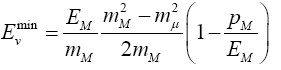
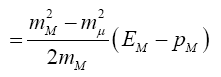
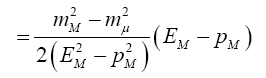
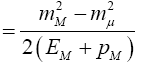
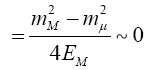
and
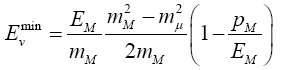
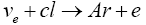
=0.427Eπ for pions
=0.954EK for kaons
where we assume that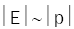 
. Therefore the neutrino spectra from conventional beams have two components, with the
lower energy parts of the beam arising from pion decay, and the higher energy parts from kaon decay. Neutrino beams can be
built to generate neutrinos anywhere between 10 MeV to hundreds of GeV. The scale ultimately depends on the energy of the
proton beam. The higher the beam energy, the higher the meson energy and the higher the neutrino energy. This section covers
the results of cross-section measurements for neutrino-nucleus interactions from a few MeV to a 100 GeV of energy by using
mono-energetic, single favour neutrino beams with different targets. The events have been generated using NuWro and emphasis
has been laid on experimental findings for comparison at different stages of analysis. We have begun plotting our results from the
threshold energy values of a few MeV to look for electron-neutrino cross-sections for their interactions with oxygen as shown in Figure 1. The choice of target is because it is an abundant gas in the atmosphere. The cross-sections so obtained are very feeble.
Figure 1: Electron-neutrino cross-sections with Oxygen using NuWro.
The Home stake experiment in USA [16] which was the earliest to detect electron-neutrinos involved the following reaction
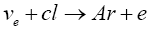
Wherein the number of electron-neutrinos detected per day was determined by the number of Argon atoms produced. The average cross-section for E>0.82 MeV was found out to be of the order of 10 45 cm2=cl atom. With this small cross-section it was not a surprise to see that only 0.17 such conversions took place per day.
The subsequent experiments such as SNO [17], which have independently measured the solar neutrino flux with greater precision, have essentially, concluded that the solar neutrinos, which are all of electron type, do not oscillate as far as the fight length is less than the diameter of earth. Moreover, it has been found that whereas the matter affects are quite large for ve→ vμ and ve→ vτ oscillations but in vacuum the oscillation probability of electron-neutrinos to other favours is reduced to 50% [18]. Thus, not much of the reason for the lower value of electron-neutrino cross-sections in the first few MeVs of energy could be attributed to their oscillations from sun to earth.
In vacuum, the neutrino oscillation probabilities are a function of the inverse of the neutrino energy. Therefore the current and next generation accelerator-based neutrino experiments such as MINOS [19] are focussing on neutrino energies of a few hundred MeV to a handful of GeV. The plot drawn in Figure 2 gives our cross-section measurements in the first 100 MeVs of electronneutrino energy with water (which is also the choice of target in some experiments [20] for being cheap and abundant). The trend of simulated cross-sections so obtained is much in conformity with the experimental results obtained with different targets [21].
Figure 2: ve QE interactions with water using NuWro.
There are a host of nuclei that are under experimental study eg; the proton beam stops at the Los Alamos Meson Physics Facility [22] have been utilized to study low-energy neutrino cross-sections on 127I. Cross-sections on iron targets have also been explored with low-energy beams at the KARMEN experiment [23]. The neutrino beam in both experimental facilities is provided from proton beam stops. High-energy proton collisions on a fixed target produce a large π+ flux which is subsequently stopped and allowed to decay. The majority of low-energy neutrinos are produced from the decay at rest from stopped μ+ and π+, providing a well-characterized neutrino beam with energies below 50 MeV. However, the main uncertainty affecting these cross-section measurements stems primarily from the knowledge of the pion flux produced in the proton-target interactions.
The study of neutrino interactions in the few-100 MeV range are relevant for supernova neutrinos, burst and relic neutrinos, solar neutrinos and low energy atmospheric neutrinos. Low-energy neutrino cross-sections feature prominently in a variety of model-building scenarios. Precise knowledge of the inclusive and differential cross-section feeds into reactor neutrino analysis, supernova modelling, neutrino oscillation tests, and countless others. Yet, the number of direct experimental tests of these cross-sections is remarkably few. In our cross-section measurements with NuWro, we see that the neutrino-nucleus interactions at threshold energies proceed through quasi-elastic scattering only. How-ever at 140 MeV, some more interaction channels start appearing on the scene and become significant towards first few Gev. The understanding of neutrino-nucleus interactions around 1 to 2 GeV energy is of great importance in analyzing neutrino oscillation experiments. This energy range is also of particular interest for being a cross over region, where the different important interaction channels turn on and o, ranging from elastic and quasi-elastic scattering (QE), through single pion production via resonance excited scattering (RES) and runs into deep inelastic scattering (DIS).
Therefore we have simulated the neutrino interactions through these three key processes for energies less than 2 GeV and have plotted the cross-sections for muon-neutrino interactions with Carbon Nucleus. Both the charged current and neutral current reaction values have been looked for in each process. The trends so obtained corresponding to these processes viz; QE, RES and DIS have been shown in Figures 3-5 respectively.
Figure 3: vμ QE interactions with carbon using NuWro.
Figure 4: vμ RES interactions with carbon using NuWro.
Figure 5: DIS interactions with carbon using NuWro.
At 1 GeV of neutrino energy, we are also in a transition region where QE and RES processes dominate but where there is also a significant DIS component being switched on as we increase the energy.
A fourth channel of interaction for coherent pion production (COH) as shown in Figure 6 has also been plotted in our results although its cross-sections are feebler than the other three.
Figure 6: vμ COH interactions with Iron using NuWro.
Therefore, for the measurement of COH cross-sections, we have used a heavier target i.e. iron and increased the energy range up to 50 GeV but the process does not show any significant improvement in the cross-sections. Charged current coherent pion production is a rare and poorly understood neutrino interaction. In this process a neutrino scatters o an entire nucleus coherently and produces a very forward-going pion and transfers little or no energy to the nucleus. The neutral current analog is a background with large uncertainties for electron appearance oscillation measurements [24]. On the other hand, the charged current analog has only been seen until recently at high energy neutrino experiments but not at the 1 GeV experiments like K2K.
The bulk of our discussion has centered on measurements of -nucleon scattering. Many of these arguments also carry over to scattering, except for one key difference that the energy threshold for the reaction is severely altered because of the large lepton mass [25]. The muon-neutrinos are also preferred over electron-neutrinos in experimental studies because of their greater abundance than the later. However, the cross-section formulae for the electron and tau-neutrinos are the same as for muonneutrinos.
There are adequate theoretical descriptions of quasi-elastic, resonance mediated, and deep inelastic scattering that have been formulated during all these years, however, there is no uniform description which globally describes the transition between these processes or how these should be combined. Moreover, the full extent to which nuclear e ects impact this region is a topic that has only recently been appreciated.
At the energies of T2K and NOvA, the quasi-elastic processes constitute a large fraction of the signal population. These are characterised by the appearance of a lepton and a nucleon in the final state.
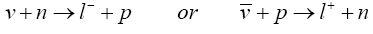
There has been a renewed interest in the measurement and modelling of QE scattering on nuclear targets. In such situations, the nucleus is typically described in terms of individual quasi-free nucleons that participate in the scattering process. Most of the neutrino experiments use a relativistic Fermi-gas model [26] when simulating their QE scattering events, although many other independent particle approaches have been developed in recent years that incorporate more sophisticated treatments.
The next most important process is the charged pion production. For a Cerenkov detector experiment or a time projection chamber (TPC), this process can pose as a background since the pion goes undetected as it can be absorbed in the nucleus before it ever reaches the active detector material and can therefore cause ambiguities in neutrino energy measurements. Charged pions are either absorbed or get converted into neutral pions via:
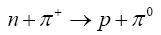
The neutral pion production, while although less probable than charged pion production can still contribute a back-ground in electron-neutrino appearance searches and must be well-simulated. Finally, deep inelastic scattering (DIS) events can also contribute a copious source of neutral pions which may contaminate an electron-neutrino appearance measurement and hence these channels must be well understood. As a result of these competing processes, the products of neutrino interactions include a variety of final states ranging from the emission of nucleons to more complex final states including pions, kaons, and collections of mesons. Moreover the cross-sections for neutrino-nucleon scatterings are not so precisely known as for leptonic reactions. This is due to the poor theoretical knowledge of the nucleon form factors.
Out of the three important interaction channels viz; quasi-elastic scattering (QE), single pion production (SPP) through resonance excited scattering and deep inelastic scattering (DIS), the later dominates the other two completely at intermediate and higher energies. This is because up to a few GeVs, the neutrino scattering takes place from composite entities such as nucleons or nuclei but given enough energy, the neutrinos can actually begin to resolve the internal structure of the target. Moreover, as we transit from low-energy neutrino interactions to higher energies, our approach are primarily focussed on the scattering of a particular target in any state and whether that is a nucleus, a nucleon, or a parton. This approach is not accidental, as it is theoretically a well-defined problem to have the target constituents treated individually. Therefore it is to be acknowledged that the approach is also limited, as it is not able to incorporate the nucleus as a whole. This is the reason that the domains of low-energy and high energy physics appear so disjointed in both approach and terminology. Until a full, comprehensive model of the entire neutrinotarget interaction is formulated, we are constrained to follow this approach. While as the description of the low energy regime exploits approaches like the elementary particle theory, effective eld theories or microscopic models such as the Shell Model, the Fermi gas is the basis for theoretical description in the high energy regime. The most common high energy interactions proceed through deep inelastic scattering (DIS) where the neutrino scatters off a quark in the nucleon via the exchange of a virtual W± or Z0 boson producing a lepton and a hadronic system in the final state. Quarks cannot be individually detected as these recombine quickly and thus appear as a hadronic shower denoted by X.
The Figure 7 shows our cross-section measurements for DIS process with iron and protons as targets. A linear dependence of the cross-sections on neutrino energy which is exhibited in the higher ranges is a con formation of the quark parton model predictions. This is because as the energy increases, the neutrino begins to probe the nucleus up to nucleon degrees of freedom. There is a point like scattering (one to one interaction) by the quarks which leads to a linear dependence of neutrino crosssections. This linearity breaks down at low energies because of sensing of nuclear effects by the projectile. For QE and RES processes, the cross-sections saturate towards increasing energies as shown in our measurements by Figure 8 for a heavier target (Iron) and by the Figure 9 for a lighter target (oxygen).
Figure 7: vμ interactions with Iron and protons for charged current DIS process.
Figure 8: Cross-section saturation for vμ interactions with Iron using NuWro.
Figure 9: Cross-section saturation for vμ interactions with oxygen using NuWro.
As expected, we observe a linearly rising cross-section that is damped by the form factors at higher neutrino energies. What is not expected is the disparity observed between recent measurements which are largely due to the nuclear e ects beyond the impulse approximation approach. Such e ects are sizeable, not well known, and ultimately complicate the description of neutrino interactions.
In the past years, a number of new results have been released on each of the above mentioned interaction channels by using several different target nuclei. These results are often not in agreement with theoretical predictions even from those anchored to deuterium or hydrogen measurements. The new measurements have started to give new hints to the theorists about the need to improve the theoretical description of neutrino interactions, which will ultimately pave the way for precision oscillation measurements. Neutrino experiments have therefore begun to re measure the absolute QE scattering cross-sections by making use of more reliable incoming neutrino uses made available in modern experimental setups.
In studying the neutrino-nucleus interaction processes, we are assuming the nucleus to be composed of quasi-free nucleons (Impulse Approximation Scheme), like in the Fermi Gas (FG) model. The typical values of momentum transfer are large enough in the 1 GeV energy regions and hence the Impulse Approximation can be used as a reliable approximation. However, in inclusive neutrino measurements there is always a significant fraction of low momentum transfer for apparently CCQE events and one cannot be sure that these are described in the proper way. A remedy for this problem can be to impose suitable cuts in momentum transfer. Thus for an experimentalist it becomes quite obvious to look for QE-like events specified by a condition that there are no mesons in the final state.
Uncertainties and Projections
As neutrinos have no other property, these had to have mass which changes to make for another favour. But what if there is some property other than mass which changes to give different favours. Discovering of that property may project neutrinos as candidates for dark energy rather than the dark matter. There are some important arguments in favour of thinking on this line of approach. One is that neutrinos are not currently the favourite of cosmologists as solutions to dark matter problem, since in their calculations these do not cluster enough. Other is that by assigning them a mass we are leaving the decay to remain unaccounted for the violation of conservation of mass. Yet another indication is that from the extremely small values of neutrino interaction cross-sections with matter, throughout, from lower to higher energies which may have some deep implications. There is also a remarkable coincidence in nature
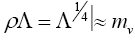(3)
where is the time independent dark energy density and is the cosmological constant. The question is if there is a relationship between the energy of empty space and the neutrinos?
One possibility is to view dark energy as the latent heat associated with a first order transition that has not yet been completed. If the latent heat is associated with a potential and a scalar eld undergoing spontaneous symmetry breaking (giving mass to neutrinos in the process), then there might be a natural explanation for the coincidence described above.
The relic neutrinos can be seen as the candidates for natural Dark Energy if these interact through a new force mediated by a light scalar eld of the dark sector. This idea is quite appealing and is substantiated by a host of arguments. Neutrinos are the only fermions which do not have right-handed components and since the discovery of neutrino oscillations, a deeper understanding of the neutrino sector including the origin of neutrino masses requires physics beyond the Standard Model. If the lepton number is violated, left-handed neutrinos are generally assumed to mix with dark right-handed neutrinos thereby acquiring small masses through the seesaw mechanism. Hence by these means the neutrinos are uniquely capable of opening a new window to the dark sector. Moreover, the scale relevant for neutrino mass squared differences as determined from neutrino oscillation experiments, m2 (10 2eV) 2, is of the order of the tiny scale associated with the Dark Energy density, (2 10 3eV) 4.
On the other hand, the cosmological constant term also significantly improves the agreement between theory and observation, the most spectacular example being the recent e ort to measure how much the expansion of the universe has changed in the last few billion years. Generically, there is a competition between two opposite forces viz; the gravitational pull exerted by the matter in the universe and the expansion imparted by the Big Bang. In an e ort to measure how much the universal expansion has slowed over the last few billion years, it has become practical for astronomers to observe very bright rare stars called supernova. The results of these observations indicate that the universal expansion is speeding up, or accelerating. With these preliminary results, raises the possibility that the universe contains a bizarre form of matter or energy that is, in effect, gravitationally repulsive. This so far unknown source of energy which has to be homogeneously distributed, can at best be slowly-varying with time in order to cause the observed late-time acceleration, and must be characterized by a negative pressure to counteract gravity. The cosmological constant is an example of this type of energy. However, much work remains to elucidate this mystery.
This work is an attempt to present a comprehensive study on neutrino-nucleus interaction cross-sections. Our discussion ranged from MeV to GeV energy scales and therefore spanned a broad range of underlying physics processes, theoretical calculations, and experimental measurements. This energy range is important because the naturally occurring solar and atmospheric neutrinos t in this energy range. Whereas atmospheric neutrinos carry MeVs of energy, the atmospheric neutrinos fall in the GeV range. To study neutrino-nucleus interactions in the first few MeV to a 100 GeV energy region, we generated a mono-energetic single favour neutrino beam at every new stage of analysis. The present study is to some extent useful for improving underground detectors discovery potential for determining the neutrino properties. One of the most straightforward approaches to have an understanding of the various characteristics of neutrinos is to investigate their interactions with nuclei. Keeping in view the importance of such studies, an attempt has been made in the present study to measure the cross-section for various neutrino interactions processes with different targets. The results serve to test the predictions of the Rein Sehgal model and verify old experimental measurements. While our results do not improve on precision, these serve as a useful cross check in a region with few measurements. Therefore more interaction channels we can measure and the more different nuclei we can test, the better we can understand both neutrinos and the nuclei with which these interact.
We are highly grateful to Sobczyk J of the Institute of Theoretical Physics, Wroclaw, Poland for fruitful communications with him from time to time which lead to initiate this type of study at University of Kashmir.