PRIVACY PRESERVING IN DISTRIBUTED DATABASE USING DATA ENCRYPTION STANDARD (DES)

Jyotirmayee Rautaray; Raghvendra Kumar

PRIVACY PRESERVING IN DISTRIBUTED DATABASE USING DATA ENCRYPTION STANDARD (DES)

Jyotirmayee Rautaray¹, Raghvendra Kumar²
School of Computer Engineering, KIIT University, Odisha, India¹
School of Computer Engineering, KIIT University, Odisha, India²

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

Distributed data mining explores unknown information from data sources which are distributed among several parties. Privacy of participating parties becomes great concern and sensitive information pertaining to individual parties and needs high protection when data mining occurs among several parties. Different approaches for mining data securely in a distributed environment have been proposed but in the existing approaches, collusion among the participating parties might reveal responsive information about other participating parties and they suffer from the intended purposes of maintaining privacy of the individual participating sites, reducing computational complexity and minimizing communication overhead. The proposed method finds global frequent item sets in a distributed environment with minimal communication among parties and ensures higher degree of privacy with Data Encryption Standard (DES). The proposed method generates global frequent item sets among colluded parties without affecting mining performance and confirms optimal communication among parties with high privacy and zero percentage of data leakage.

Keywords

Distributed data mining, privacy, secure multiparty computation, Frequent Item sets, Data Encryption standard (DES).

INTRODUCTION

Data mining techniques is extract useful information for considered decision making from transactional dataset which is either centralized data base or distributed data base. The term data mining refers to extract or mine knowledge from an enormous amount of data. Data mining functionalities similar to association rule mining, cluster analysis, classification, prediction etc. specify the different kinds of patterns mined. Association Rule Mining [1] [2] [3] [4] [5] finds exciting association or correlation among a large set of data items. Finding association rules among huge amount of business transactions can help in making many business decisions such as index design cross marketing etc. A best example of Association Rule Mining is market basket analysis. This is the process of analysing the client buying behaviour from the association between the different items which is available in the shopping baskets. This analysis can help retailers to increase marketing strategies. Association Rule Mining involves two stages

(i) Finding frequent item sets from a given transactional data set

(ii) Generating strong association rule between the two or more attributes

But the Association Rule Mining take more number of steps to find the Association Rule between the two attribute. so the complexity Is also increased. That’s why in this paper we used FP Tree algorithm [5] [6] [7] [8] which is advancement to the Association Rule Mining. In this the number of step is very less as compared to Association Rule Mining. And it’s very easy to find the Association Rule between the given transactional item sets. Algorithm shows how to extract frequent item sets from a given transactional data set

Algorithm: - FP grouth

Allows frequent item set without candidate item set generation. This is two step approaches Step1:-Design a compact data structure called the FP tree using the 2 passes over the given data set. Step2:- Extract frequent item sets from the FP tree this frequent item is extract after the traversing through FP tree.

A. Distributed Data Mining

Distributed Data Mining [5] [6] [13] [14] is measured as the exact solution for many applications, as it reduces several practical problems like huge data transfers, huge storage unit requirement, security or privacy issues etc. Distributed Frequent Rule Mining is a sub-area of Distributed data mining. Let D1, D2… Dn is data sources which are physically distributed. Let n be the number of items and I = {i1, i2…in} be a set of items. Global Support of an item set is defined as the ratio of the number of occurrences of the item set in all the data sources to the whole number of transactions in all the data sources. An item set is said to be globally frequent when the number of occurrences of that particular item set in all the data sources is larger than a user-specified minimum support. During global frequent item set generation, local frequent item sets of entity party need to be shared. So, the participating parties learn the exact support count of all other participating parties. However, in many situations the participating parties are not interested to release the support counts of some of their item sets which are considered as sensitive information. Thus, it is essential to share information pertaining to an entity data source without revealing sensitive information. Fig 1 shows the how the frequent rule mining finds the global rule in distributed database.

B. Secure Multi Party Computation

Secure Multi Party Computation [7] [8] [9] [10] solutions can be applied to maintain privacy in distributed rule mining. The main goal of Secure Multi Party Computation in distributed rule mining is to find global frequent item set without disclosing the local support count of participating sites to each other. In distributed privacy preserving data mining, the participating sites may be treated as honest, semi-honest. The semi-honest parties are honest but try to learn more from received information. Secure Multi Party Computation worked both real and ideal model this is very useful more than two parties to compute their global result without disclosing the individual result. In real model there is no any existence of the trusted third party but in Ideal model there is existence of trusted third party.

C. Data Encryption standard for Two Key

Some researchers suggest double encryption [14] [15] that provide the high privacy to the database. The working of double encryption is as following. First consider two secrete key or random number Like Key1 and Key2. After that encrypt the first party data set using the key 1 value and after that the second that encrypted data set to the next party presents in the network and after that encryption the second party data set uses the second secrete key or second random number. so after that the data set is fully encrypted its becomes impossible to the hacker to hack that particular data sets. Fig2 shows the working step of data encryption standard in two key value cases.

II. IMPLEMENTATION AND RESULT

In this implementation [10] [11] consider two different databases represented as Party P1 and Party P2 having minimum support count is 40 % and first calculate the partial support by using the following formula Partial support= X. support- Minimum support*|size of the database| and after that we calculate the global excess support by using the following formula that’s is global excess support= Total partial support – key value. If global excess support if greater than zero it means that’s its globally frequent item sets otherwise infrequent item set. Table 1 and Table 2 represent the data sets for party 1 and 2

STEP2:-

A1:3, A2:2, A3:2, A4:2, A5:1, A6:2

STEP3:-SORT IN DESENDING ORDER

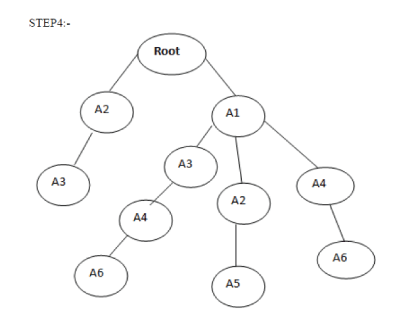
A1:3, A2:2, A3:2, A4:2, A6:2, A5:1

STEP5:- A1= {(A1:3)} A2= {(A2:1), (A1:1)} A3= {(A2:1) (A1:1)} A4= {(A3:1, A1:1), (A1:1)} A5= {(A2:1, A1:1)} A6= {(A4:1, A3:1, A1:1) (A4:1, A1:1)}

STEP6:- A4= A1:2, A6= (A4:2, A1:2)

STEP7:- A4A1:2, A6A4:2, A6A1:2 STEP8:- SUPPORT (A4, A1) = COUNT (A4, A1)/T=2/4=O.5=50% SUPPORT (A6, A4) = COUNT (A6, A4)/T=2/4=O.5=50% SUPPORT (A6, A1) = COUNT (A6, A1)/T=2/4=O.5=50% CANDIDATE SET = {A1, A4, A6}

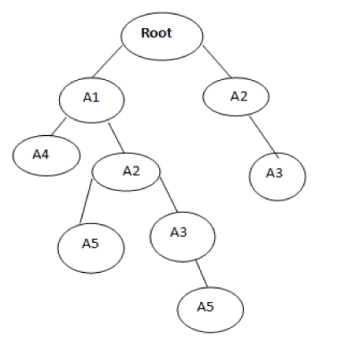
STEP5:-

A1= {(A1:3)}

A2= {(A1:2), (A2:1)}

A3= {(A2:1, A1:1) (A2:1)}

A4= {(A1:1)}

A5= {(A2:1, A1:1) (A3:1, A2:1, A1:1)}

STEP6:-

A3= {A2:2}

A5= {(A2:2) (A1:2)}

STEP7:-

A3A2:2, A5A2:2, A5A1:2

STEP8:-

SUPPORT (A3, A2) = COUNT (A3, A2)/T=2/4=0.5=50%

SUPPORT (A5, A2) =COUNT (A5, A2)/T=2/4=0.5=50%

SUPPORT (A5, A1) = COUNT (A5, A1)/T=2/4=0.5=50%

SUCH THAT CANDIDATE SET- {A1, A2, A3, A5}

At party P1 the number of candidate item sets is {A1, A4, A6} At party P2the number of candidate item sets is {A1, A2, A3, A5} Let us consider the item set {A1} So that the partial support of party P1 is calculated by using the following formula Ps1= X. support- minimum support*|size of the database| Ps1=3-.4*4=1.4 So that the partial support of party P2 is calculated by using the same formula given above Ps2=3-.4*4=1.4 So that each party has their own partial support value then after that for providing the high privacy used random number or key value let the for party P1 have the key value is 1 and for party P2 have the key value 1 , after that encrypt the each party database by using the key value then the party party P1 send the value to the party P2 is Ps1+key value1=1.4+1=2.4 and the party P2 receive that value and adds its own partial support as well as the key value such that the party P2 send the value is Ps1value +Ps2+ Key value2=1.4+1+2.4=4.8 so that the global excess support is GES=Ps2-Key value=4.8-1-1=2.8 so that global excess support greater than zero it means that its globally frequent item sets.

III. CONCLUSION

Privacy preserving data mining techniques for distributed database environment have been studied and algorithm for finding global frequent item sets has been proposed and implemented. It is found that the proposed method securely determine global frequent item sets with minimal communication and time complexity. Secure multi party computation is used for global frequent item set generation. In this implemented work we provide the highest privacy to the database with zero percentage of data leakage but this is applicable for homogeneous database but in future this extended in heterogeneous database.

Tables at a glance


Table 1	Table 2

Figures at a glance


Figure 1	Figure 2

References

Agrawal, R., et al.: Mining association rules between sets of items in large database. In: Proc. of ACM SIGMOD’93, D.C, pp.207-216, 1993.
Agarwal, R., Imielinski, T., Swamy, A.: Mining Association Rules between Sets of Items in Large Databases. In Proceedings of the 1993, ACM SIGMOD International Conference on Management of Data, pp. 207-210, 1993.
Srikant, R., Agrawal, R.: Mining generalized association rules. In: VLDB’95, pp.479-488, 1995.
Agrawal, R., Srikant, R.: Privacy-Preserving Data Mining. In: proceedings of the 2000 ACM SIGMOD on management of data, pp. 439-450, 2000.
Lindell, Y., Pinkas, B.: Privacy preserving Data Mining. In: Proceedings of 20th Annual International Cryptology Conference (CRYPTO) 2000.
Kantarcioglu, M., Clifton, C.: Privacy-Preserving distributed mining of association rules on horizontally partitioned data. In IEEE Transactions on Knowledge and Data Engineering Journal, IEEE Press, Vol 16(9), pp.1026-1037, 2004.
Han, J. Kamber, M.:Data Mining Concepts and Techniques. Morgan Kaufmann, San Francisco, 2006.
B., Mishra, “Hybrid technique for secure sum protocol”. WCSIT, Vol 1, pp.198-201, 2011.
Sugumar, Jayakumar, R., Rengarajan, C.:Design a Secure Multi Site Computation System for Privacy Preserving Data Mining. In International Journal of Computer Science and Telecommunications, Vol 3, pp.101-105. 2012.
Muthu Lakshmi, N. V., Sandhya Rani, K.: Privacy Preserving Association Rule Mining without Trusted Site for Horizontal Partitioned database. In International Journal of Data Mining & Knowledge Management Process (IJDKP) Vol.2, pp.17-29, 2012.
Muthu lakshmi, N.V., Sandhya Rani, K.: Privacy Preserving Association Rule Mining in Horizontally Partitioned Databases Using Cryptography Techniques. In International Journal of Computer Science and Information Technologies (IJCSIT), Vol. 3 (1) , PP. 3176 – 3182, 2012.
Goldreich, O., Micali, S. & Wigerson, A.: How to play any mental game. In: Proceedings of the 19th Annual ACM Symposium on Theory of Computing, pp.218-229.
Franklin, M., Galil, Z. & Yung, M.:An overview of Secured Distributed Computing. Technical Report CUCS- 00892, Department of Computer Science, Columbia University.
Dehao C. “Tree Partition based Parallel Frequent Pattern mining on Shared Memory Systems” IEEE.
Charles p. pfleeger, shri Lawrence pfleeger “security in computing”2011.