ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Alireza Rezaee,1, Azizeh Ajalli 2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper, new genetics and Ant colony optimization algorithm for solving the problem of graph correspondence is presented. When using the genetics technique for the problem of graph correspondence, it is not easy to define the crossover operator. our attempt will be to present a definition holding the integration of the population graph in a one-to-one correspondence. we present new and suitable definitions for the target function and a function giving score to a solution at the end of any cycle. We compare both algorithms and try to find their advantages and their shortcomings.
Keywords |
| Graph Correspondence, Genetics Algorithm, AOC Algorithm |
I. INTRODUCTION |
| The problem of graph correspondence has been noticed in a wide range of various fields and has become an important instrument for modeling and solving different problems. This problem is a NP-Complete one and the time required for solving it increases exponentially in terms of the number of the input graphs. Recently, many researches are conducted for improvement of the efficiency of graph correspondence algorithms, both in time and in memory consumption. Some of these algorithms reduce temporal complexities through applying limitations over the structure of the input graphs. Another method for reducing the complexity of the process of correspondence is to present a special display for seeking and deleting useless routes of the search space. In these methods, no limitation is applied on the structure of the input graphs. So they can be used in a larger domain of applications. One of the first articles in this context [1] suggests an algorithm applying some distortion on the input graphs and builds an intermediate display on which the action of correspondence is done much rapider. But [2] showed that the assumptions used by this method are not always true and this limits the domain of using this algorithm. |
| Another method reducing the search space considerably is Ullmann algorithm that uses backwards technique [3] and is still widely used. Messmer in [4] compared this algorithm with other algorithms and showed its high efficiency in a one-to-one correspondence. |
| Another algorithm using backwards techniques is Schmidt& Druffel algorithm stated in [5]. This algorithm uses the information existing in the distance matrix. Another important algorithm in graphical correspondence is Mckay's Nauty algorithm [6]. This algorithm is based on a series of transformations. These transformations transform the graphs to a focused form and correspondence test is much rapider in this focused form. |
| Another algorithm for the problem of graphical correspondence is presented in [7]. In this algorithm, instead of trying to reduce temporal complexity of the algorithm, it is tried to reduce the complexity in a case there is a constant model graph and the graphs are constantly passed in front of this model graph and the samples of the model graph are extracted from any target graphs. Since the model graph is deemed constant in this algorithm, so a table of information related to the model graph and the various states of having it in the target graph can be built in a preprocessing manner and it can be used in the process of correspondence. |
| Using techniques inspired from the nature in the problem of graph correspondence is examined in several articles. [8] suggested a method for solving the problem of graph correspondence using the genetics algorithm. In his suggestion, the suggested crossover function may not work correctly for a one-to-one correspondence. The example he used for testing the algorithm is the examination of the resemblance between the solar system and an atom. In his work, no comparison between the suggested algorithm and other methods has been done. In [9], using an ACO technique, a method for solving the problem of graph correspondence is suggested. In this article, definitions of the target function and also a function giving scores to a solution found at the end of any cycle are stated. [10] has also proposed an algorithm using ACO. |
| At first, we try to improve genetics and ACO algorithms suggested for the problem of graph correspondence. For genetics algorithm, we present a new definition of crossover operator. [11]For ACO algorithm, we try to present exact definitions fitting the problem of graph correspondence for the target function and a function giving scores to a solution at the end of any cycle. Finally, we do a comparison between the two proposed methods. [12] The structure of this article is as follows: first, we propose the genetics algorithm suggested for solving the problem of correspondence. [13,14]Then, we describe the proposed method using ACO technique. In the next section, the results are examined and both algorithms are compared. Finally, conclusions are derived from the works. [15,16] |
II. GENETICS ALGORITHM |
| Genetics algorithm is an optimizing algorithm based on using evolutionary methods. The main idea of this algorithm is that instead of a solution, a population of solutions is held for a problem of optimization and doing operations over this population, the new population is generated. Any solution is composed of a set of genes and any gene shows one or more properties fitting that solution. Genes can be of any type of data, but they are often considered as binary ones. Any solution forms a vector of binary values although except the vector, other data structures can be used (as it is done for solving the problem of graph correspondence and instead of using a vector, we use a two dimensional matrix). Any member of this population can pair based on the closeness to a target function and produce some offspring. These offspring can be a part of the new population of the solutions. After all reproductions are performed, individuals (solutions) being more beneficial to the target function than other solutions are returned as the final solution of the problem. [17] |
| Genetics algorithm has good capabilities in solving problems of discrete optimization. Naturally, genetics algorithms are suitable for solving those problems having many optimal points and in addition, having this property that sub-solutions can be locally combined and a better general solution is obtained. This is done using the crossover function. [18] |
| In the problem of graph correspondence, a correspondence function is defined identifying the relation between nodes of the target graph and those of the model graph. This correspondence function is shown as a two dimensional binary matrix M when used in Genetics algorithm. Any row of this matrix shows a node of the target graph ( i t ) and any of its columns shows a node of the model graph ( j b ). If the element ij M of this matrix is one, then f (ti ) will be equal to j b . Only an element of a row can have a non-zero value and other elements must be zero, because any node of the target graph can only correspond to a node of the model graph. |
| Now we need to define mutation and crossover operators in this representation of the problem of graph correspondence. These definitions must perform such that the integration of the matrix holds, i.e. after applying them; any node of the target graph only corresponds to a node of the model graph. For mutation, we use the shift of two rows of the matrix, i.e. in mutation of a solution (a matrix), we replace nodes of the model corresponded to two target nodes. [19] |
| Definition of crossover function is not as easy as that of mutation. Our definition from crossover function is that first, we determine a position between one to the number of the nodes of the target graph (the number of rows of the matrix). This position divides any of the two matrixes and also the matrix must be divided to two parts. The new matrix takes any parts from one of the two available matrixes. A problem we face is that the integration of the resulting matrix may not hold and nodes from the target graph correspond to some nodes from the model graph. In this case, the crossover function replaces some non-zero values of the column having more than one non-zero value with zero values of the columns not having non-zero values. [20] |
III. ACO ALGORITHM |
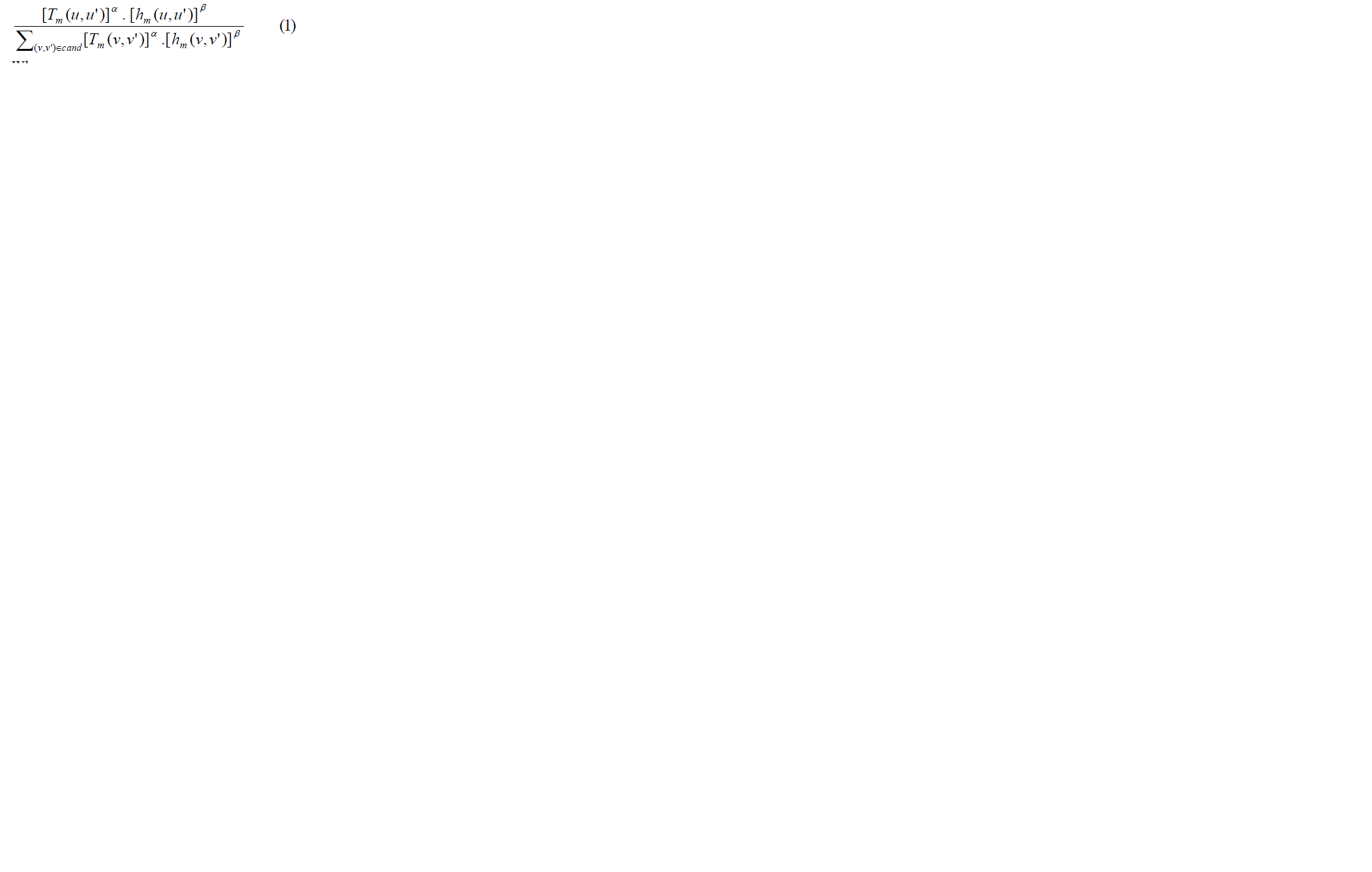 |
 |
 |
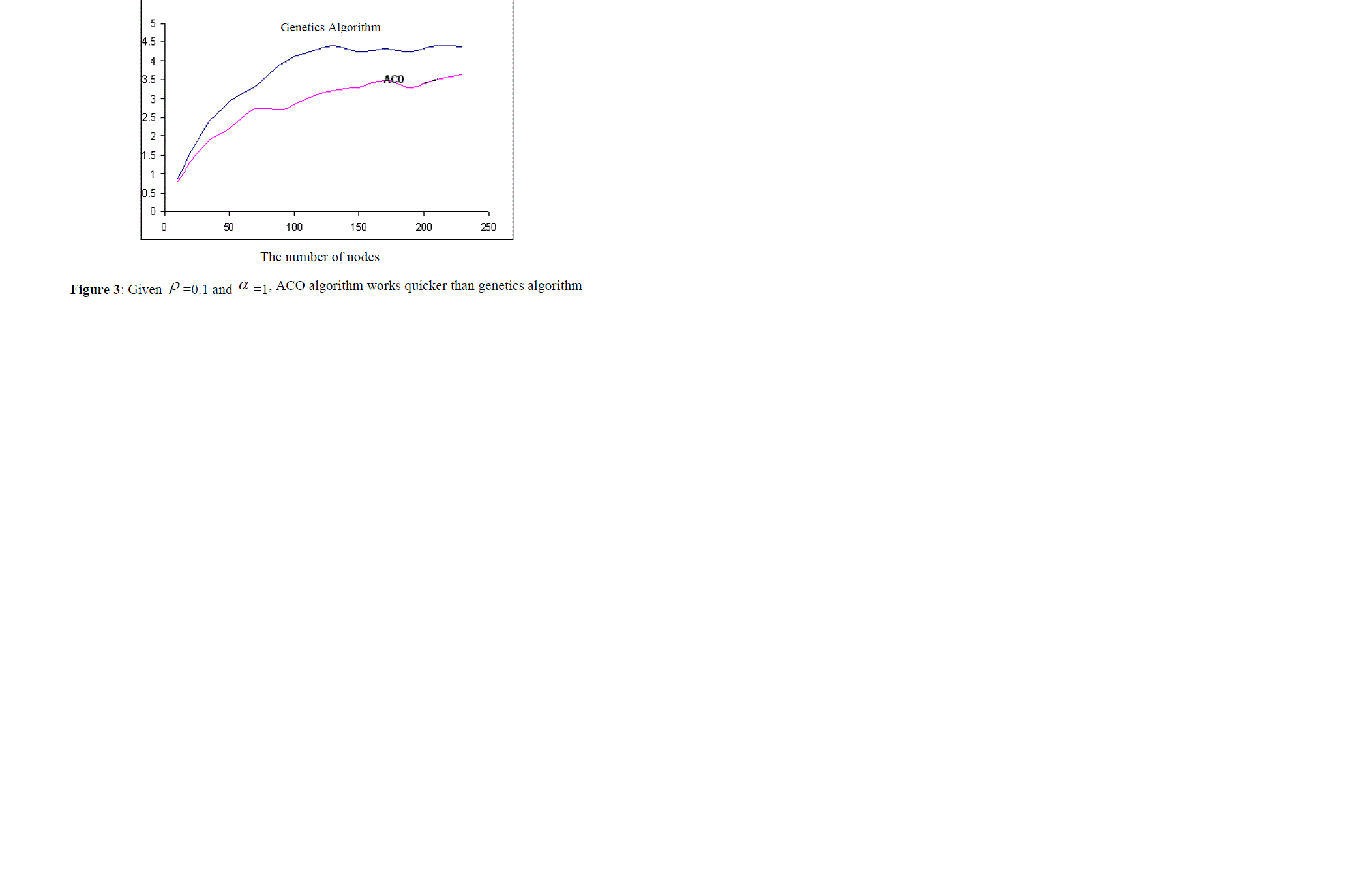 |
| Another problem is the number of the nodes existing in the graph. If the size of the graphs increase (in our experiments, more than 150 nodes), then regardless of the parameters of ACO algorithm, genetics algorithm works better than ACO algorithm. For example, consider the above case ( ïÃÂò =0.05 and ïÃÂá =0.5). in this case, when the number of nodes is low, ACO algorithm works quicker (as it is shown in figure 4), but when the number of nodes is high, genetics algorithm finds the answer quicker. |
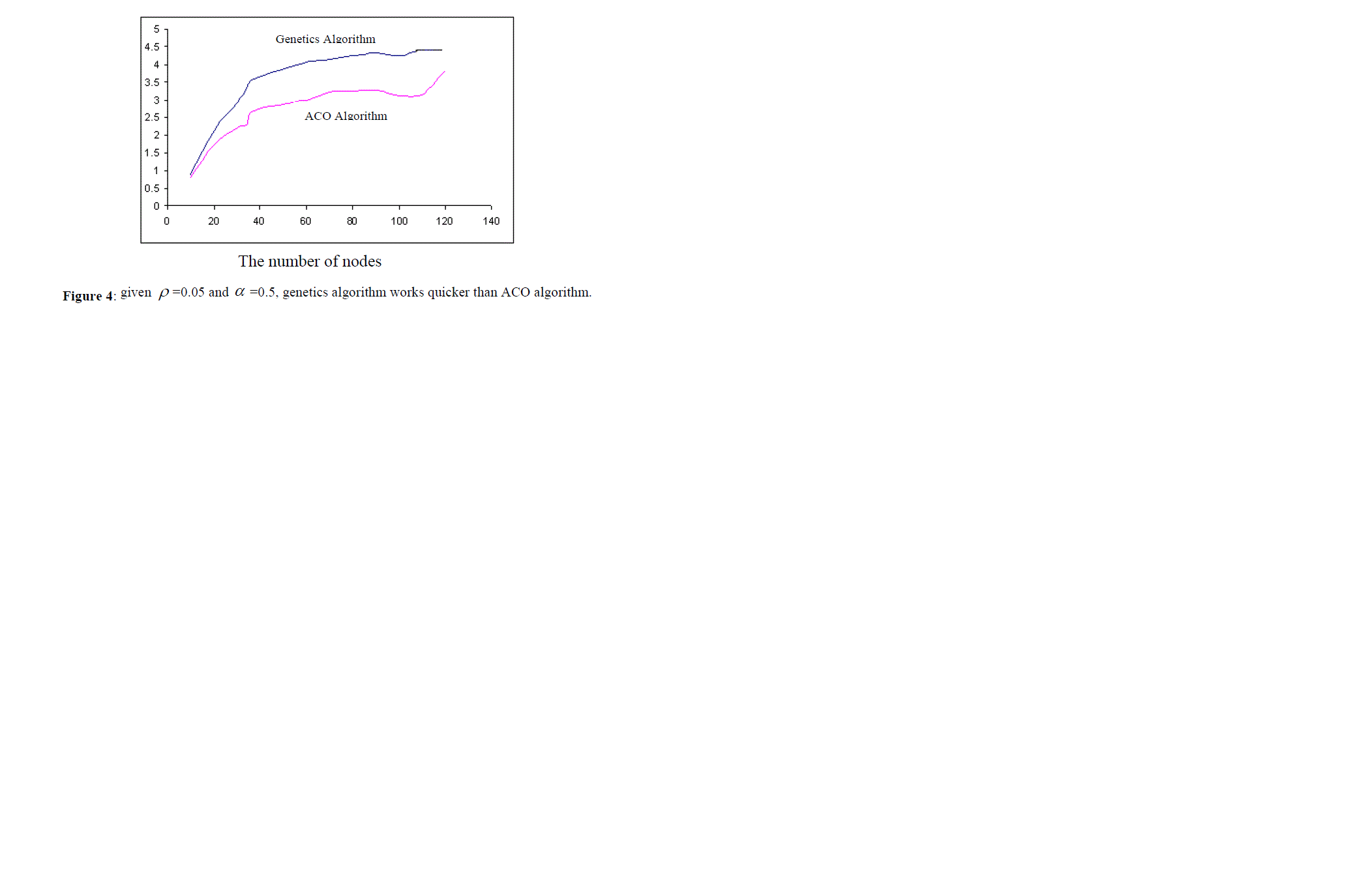 |
| The vertical axis shows the operation time. First, ACO algorithm works better, but gradually increasing the number of nodes (more than 150 nodes), the operation time of genetics algorithm becomes less than that of ACO algorithm. |
CONCLUSIONS |
| In this paper, we first presented a genetics algorithm and an ACO algorithm for the problem of graph correspondence. We stated a new definition from crossover operator in genetics algorithm that holds the integration of the population graph. In ACO algorithm, we presented new definitions for the target function and a function giving scores to a solution at the end of any cycle. |
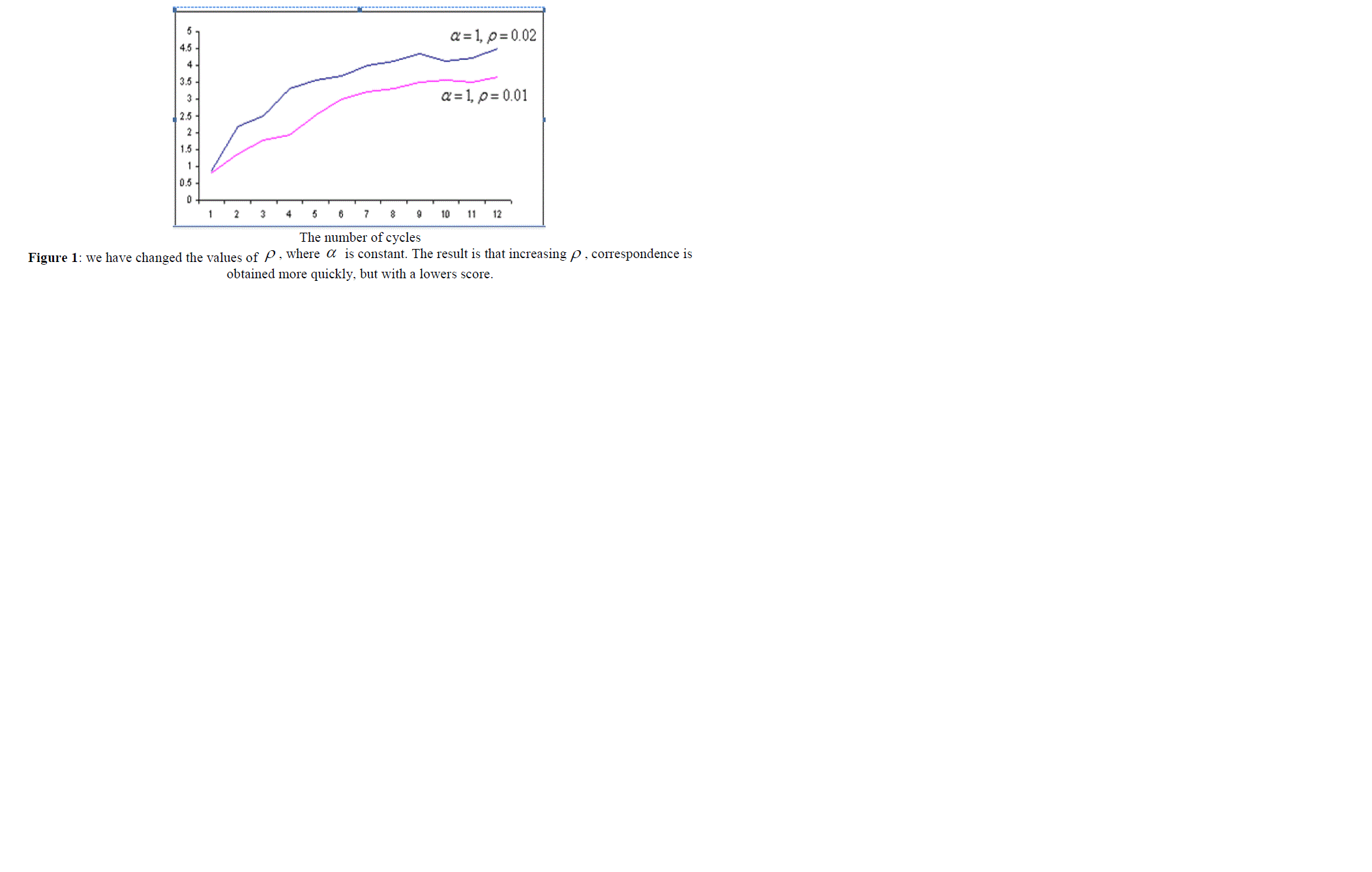
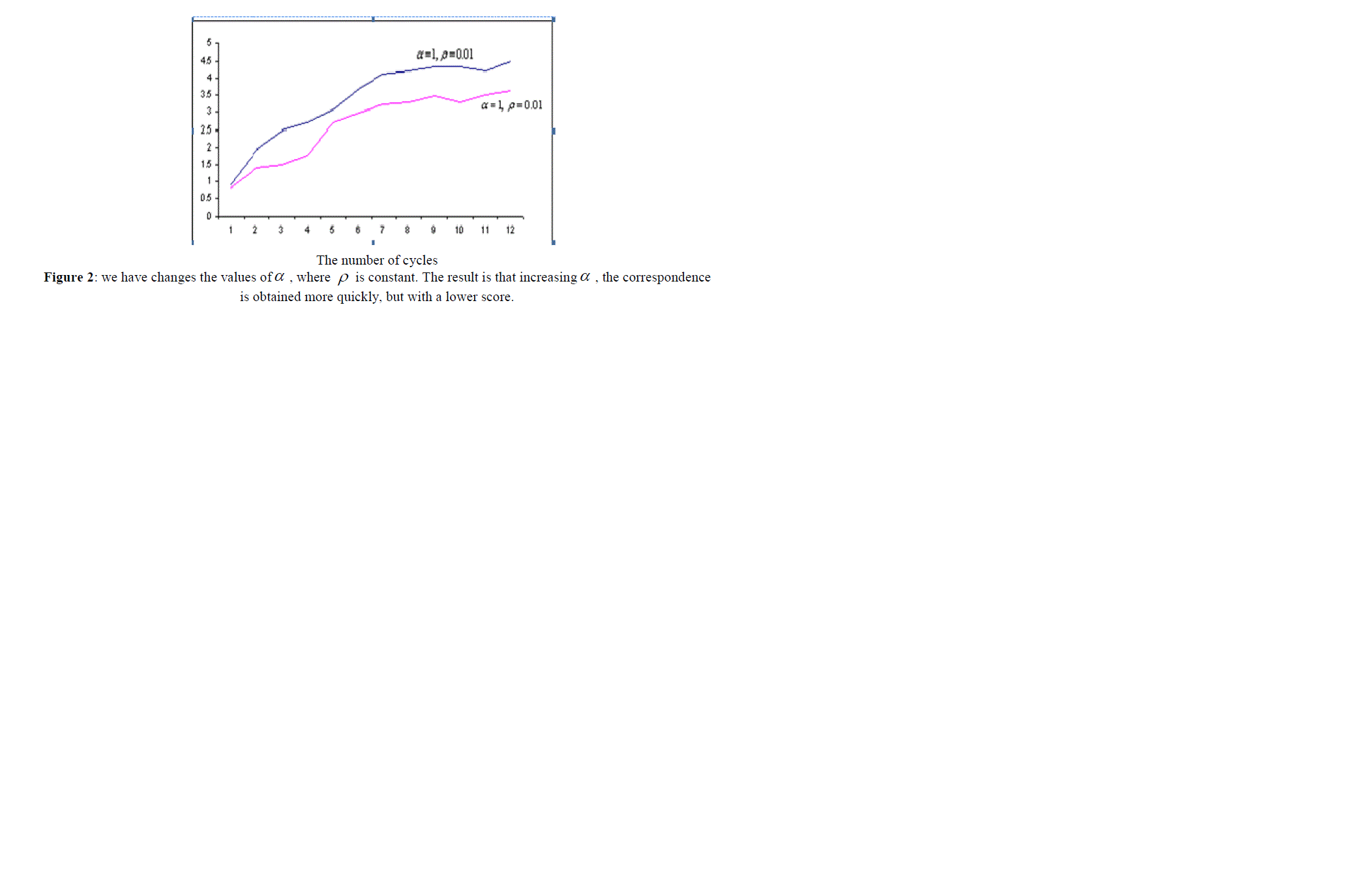
| In the next step, we compared both algorithms presented. ACO algorithm is very sensitive to the parameters ïÃÂò and ïÃÂá , and its operation time and also the quality of the solution it finds (the score it gains) depends on these parameters. This relation is presented in the section, empirical results and the comparison of both algorithms, and also in figures 1, 2, 3 and 4. |
| If the size of these graphs increases (for example more than 150 nodes), regardless of the parameters of ACO algorithm, genetics algorithm works better than ACO algorithm (it obtains correspondence in less time). |
References |
|