Noor Zaman Sheikh*
Department of Mathematics, Jana Priya High School, Guwahati, Assam, India
Received: 13-Oct-2022, Manuscript No. JSMS-22-77929; Editor assigned: 18-Oct-2022, Pre QC No. JSMS-22-77929 (PQ); Reviewed: 07-Nov-2022, QC No. JSMS-22-77929; Revised: 14-Nov-2022, Manuscript No. JSMS-22-77929 (A); Published: 21-Nov-2022, DOI: 10.4172/J Stats Math Sci.8.7.001.
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
Twin primes can be distinguished as the primes that occur with a gap of 2 between them. The estimation of twin prime is generally regarded as pertaining to the basic concept of mathematics while some considered them as fundamental mathematical problem in the number theory. This study attempts to provide a credible proof for the existence of the twin prime conjecture. Here the fundamental concept associated with the proof of the formula for the prime numbers is made use to derive the proof. In the observational space this proof was initially a difficult problem to be solved and therefore was transformed into general space for obtaining the solution. This article describes the multiplications of the twin primes in a logical manner along with the prime numbers in a systematic way following which a proof of the twin prime conjecture is provided. The study concludes that there are infinite prime numbers.
Infinite; Primes; Twin primes; Integers
Ever since the beginning of the mathematical studies, one of the major unsolved problems in the number theory was the question pertaining to existence of infinitely several twin primes [1]. The statement of the twin prime conjecture says that “there exist infinite number of primes “p” so that the formula (p+2) also represents a prime number”. De Polignac, is a mathematician who made a well-known estimation that “for all the range of natural numbers “q”, there exist infinitely multiple primes so that the formula (p+2q) also represents a prime number”. This twin prime conjecture was made in the year 1849. The twin prime conjecture represents the case when q=1 of the Polignac’s conjecture [2]. Later a relatively stronger form of twin prime conjecture evolved which is called as Hardy-Littlewoods conjecture that adds a twin prime distribution law to the existing prime number theorem. Yitang Zhang a mathematician announced a proof on April 17, 2003, that states for some integer N that is lesser than 70 million, there exists infinitely several pairs of primes that differ from 70 million and these findings were published in the Journal, Annals of Mathematics in the year 2013. Terrence Tao another mathematician also proposed a polymath approach to optimize Zhang’s bound. If the prime numbers behaved like random numbers, it won’t be difficult to comprehend that the behaviour demonstrated by Zhang is accurate. Considering the diverse claims of twin primes conjecture, one can also expect infinite pairs of primes separated by only 2 [3].
If we consider all the first “N” numbers, nearly (N/log N) of them would represent the primes which when distributed randomly, each number “n” would have a chance equivalent to (1/log N) of being a prime number. The chances of both “n” and “n+2” being prime number is approximately equivalent to (1/log N)2 . Therefore, in this context the next question arises with regard to how many pairs of prime numbers that exist which are separated by 2. There would be approximately “N” pairs or (n, n+2) of prime numbers in the range of the interest with each one having the probability equivalent to (1/log N)2 of being a twin prime. Considering these conditions, one can anticipate to find nearly N/(log N)2 numbers of twin primes in the given interval [4]. There are definitely chances of certain deviations from the pure randomness whereby the number theorists take into account these small effects. Further detailed and refined analysis by including these effects suggests that the number of twin primes should be in fact nearly 32% greater than the previously derived N/(log N)2 twin primes. Such detailed approximation leads us to the prediction that the number of twin primes that are less than a quadrillion should be approximately 1.1 trillion, the actual figure being equal to 1,177,209,242,304. As estimated by the number theorists this number of twin primes is comparatively very large. Regardless of how large the number is, this result would be still expected as there are no deep miraculous hidden structures in the process.
Theorem 1: There is an infinite number of primes.
Proof: Euclid’s proof is by contradiction. Let p1< p2< p3 < ……. be the primes in ascending order, and suppose that there is a last prime, called Pn. Now consider the positive integer P=p1p2p3……..pn+1. Because P>1, we may use the fundamental theorem of arithmetic (every positive integer n>1 is either a prime or a product of primes; this representation is unique, apart from the order in which the factors occur) to conclude that P is divisible by some prime p [5]. However, p1,p2,…..,pn are the only prime numbers; hence, p must be equal to one of p1,p2,…….,pn. Combining the divisibility relation p|p1p2…..pn with p|P, we arrive at p|P-p1p2….pn or, equivalently, p|1. The only positive divisor of the integer 1 is 1 itself, and because p>1, a contradiction arises. Thus, no finite list of primes is complete. Hence, the number of primes is infinite.
Theorem 1 is strong. We can actually identify only a finite number of primes. The largest prime currently known is 219937-1, and we do not know all of the primes smaller than this one. (A list of all the primes smaller than 10,000,000 can fill a large book.) The prime 219937-1 is a very large number: it has more than 6000 digits. Although 219937-1 is a large number, there are infinitely many integers larger than it and only a finite number that are smaller. Thus, although we can name only a finite number of primes, we may be sure that no matter how many we discover, there are infinitely more (Table 1).
| r | pr | p1p2……..pr+1 | Prime divisor |
|---|---|---|---|
| 1 | 2 | 3 | 3 |
| 2 | 3 | 7 | 7 |
| 3 | 5 | 31 | 31 |
| 4 | 7 | 211 | 211 |
| 5 | 11 | 2311 | 2311 |
| 6 | 13 | 30031 | 59, 509 |
| 7 | 17 | 510511 | 19,97,277 |
| 8 | 19 | 9699691 | 3,47,27,953 |
Table 1. Finite numbers of prime divisor.
Hence, to find a prime number larger than 219937-1 without the aid of a machine, a large amount of time at least several centuries will be needed. Euclid’s theorem is too important for us to be content with a single proof. Here is a variation in the reasoning: An infinite sequence of positive integers is formed [6].
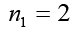
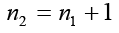
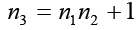
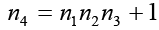
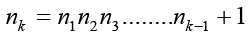
Because each nk>1, each of these integers is divisible by a prime number. However, no two nk can have the same prime divisor. To see this, let d=gcd(ni, nk) and suppose that i<k. Then, d divides ni and, hence, must divide n1n2……nk-1. Because d|nk, then d|nk-n1n2……nk-1 or d|1. The implication is that d=1, so the integers nk (k=1,2,3,…..) are pair-wise and relatively prime. The main observation that is intended to convey in this article is that there are several distinct primes in the form of nk; that is, there are infinite primes. Now, for instance the positive integers 2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61,67,71,73,79,83,89,97,101,103,107,109,113,127,131,137,139,149,151,157,163,167,73,179,181,191,193,197,199,211,223,227,229,233,239,241,251,257,263,269,271,277,281,283,293,307,311,317,331,337,347,349,353,359,67,373,379,383,389,397,…are all the prime numbers in ascending order.
Therefore, the twin primes are the primes with a gap of 2, and we can select all the following prime pairs: (3,5),(5,7),(11,13),(17,19),(29,31),(41,43),(59,61),(71,73),(101,103),(107,109),(137,139),(149,151),(179,181), (191,193),(197,199),(227,229),(239,241),(269,271),(281,283),(347,349),…. Two known twin primes are 2,003,663,613 (2195,000-1) and 2,003,663,613 (2195,000+1). We can write the inequalities by comparing the multiplication result (in ascending order) of twin primes and the primes, as shown below. Since the first two prime numbers are 2 and 3, the first twin prime pair would be (3, 5); thus, 3.5>2.3.
Similarly, for the immediate next two prime numbers 5 and 7, the twin prime pair would be (5, 7). Therefore this can be given in the pattern of 3.5.5.7>2.3.5.7.
Then for the next two prime numbers 11 and 13, the twin prime pair representation would be (11, 13). We can write the numerical representation as 3.5.5.7.11.13>2.3.5.7.11.13.
For the next two prime numbers are 17 and 19, and the twin prime pair is (17, 19). The next level of representation can be written as 3.5.5.7.11.13.17.19>2.3.5.7.11.13.17.19. Then for the next two prime numbers 23 and 29, the twin prime pair is (29, 31). This can be now written as 3.5.5.7.11.13.17.19.29.31>2.3.5.7.11.13.17.19.23.29
Similarly, for the next two prime numbers 31 and 37, (41, 43) would be the twin prime pair and can now be written as 3.5.5.7.11.13.17.19.29.31.41.43>2.3.5.7.11.13.17.19.23.29.31.37
For the next two prime numbers 41 and 43, the twin prime pair is (59, 61) separated by 2. We can write this now as 3.5.5.7.11.13.17.19.29.31.41.43.59.61>2.3.5.7.11.13.17.19.23.29.31.37.41.43. The next two prime numbers are 47 and 53, and the twin prime pair is (71, 73). The next numerical representation can be written as 3.5.5.7.11.13.17.19.29.31.41.43.59.61.71.73>2.3.5.7.11.13.17.19.23.29.31.37.41.43.47.53. So on so forth for the next two prime numbers are 59 and 61, and the twin prime pair is (101,103). This can be now written as 3.5.5.7.11.13.17.19.29.31.41.43.59.61.71.73.101.103>(2.3.5.7.11.13.17.19.23.29.31.37.41.43.47.53.59.61).
In a similar fashion by continuing the same process, we can include incrementally larger and larger primes, and we can observe large numbers of twin prime pairs. By multiplication, the inequality holds, that is, the “product of all twin prime integers in ascending order is greater than the product of all prime integers in ascending order”.
Proof: Here we reinforce the main proof with the help of a theorem that states that “there are infinitely many primes”. Let p1, p2, p3, p4, p5, p6, p7, p8,……… be prime numbers in the ascending order, and suppose there is a last finite prime, called pn. Now considering the positive integer

Clearly, x>1; therefore, the positive integer must be either a prime integer or a composite integer. It can be easily seen that pn< x. Now, if x is any prime number, then a contradiction arises because, according to our supposition, pn is the last finite prime. Hence, the number of primes is infinite. On the other hand, if x is not a prime integer, then Euclid`s proof can be used to conclude that there is an infinite number of primes.
Now, let (q1,q2),(q3,q4),(q5,q6),(q7,q8),… be the twin prime pairs corresponding to the primes p1,p2,p3,p4,p5,p6,p7,p8,p9,p10,p11,…….Clearly, q2-q1=2, q4-q3=2, q6-q5=2, q8-q7=2, ………and so on [7].
From the numerical evidence, we can write the product of the first two prime numbers and the first twin prime pairs as q1.q2>p1.p2; then, we can write q1.q2.q3.q4>p1.p2.p3.p4 and q1.q2.q3.q4.q5.q6>p1.p2.p3.p4.p5.p6 and q1.q2.q3.q4.q5.q6.q7.q8>p1.p2.p3.p4.p5.p6.p7.p8.
Continuing this process, for the existence of an infinite number of primes, there must exist twin prime pairs (qi,qj), where qj-qi=2, such that the inequality holds.
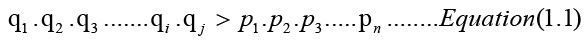
Now the inequality also holds if we add 1 on the RHS,
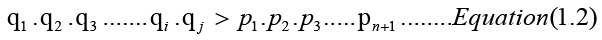
The RHS of Equation (1.2) is equal to x in Equation (1), for which we have already concluded that there is an infinite number of primes. Hence, from Equation (1.2), we can conclude that there is an infinite number of twin primes.