ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
J. M. Rudagi1, Vinayak Dalavi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
There are various simple hardware-efficient algorithms exist which can be used to increase speed while performing the desired signal processing tasks. One such simple and hardware-efficient algorithm is CORDIC which uses only Shift-and-Add arithmetic with table Look-Up to implement different functions. It can be used to efficiently implement Trigonometric and other functions. In this paper we present the conventional unrolled CORDIC architecture. The processor is designed using Verilog HDL using a structured coding method, simulated using ISIM simulator and implemented using Xilinx 14.2 FPGA synthesis Tool for 16 and 32 bit conventional radix-2 CORDIC architectures. The output of the CORDIC architectures are analyzed and verified, and compared with the actual values obtained from MATLAB.
Keywords |
| CORDIC, Cosine, Sine, Unrolled Architecture, Verilog |
INTRODUCTION |
| Most of the engineers tasked with implementing a mathematical function such as sine, cosine or square root within an FPGA may initially think of doing so by means of a lookup table (LUT), possibly combined with linear interpolation or a power series if multipliers are available. LUTs are the fastest way to make the computation; but the precision of the result is directly related to size of the look-up table. The use of power series is slow to converge to a desired precision. In effect, the look-up table size is being traded off at the expense of computation time. |
| CORDIC [1], [2], [3] method for calculating these elementary functions, is a compromise between the two methods described above wherein the precision is preserved without any considerable memory requirement. The use of the architectures in modern DSP systems [4], [5] requires a rapid increase in performance accompanied by a decrease in cost and time-to market. Higher performance is achieved by optimizing these structures for improved timing behaviour and low power consumption. FPGA provides the hardware environment in which dedicated processors can be tested for their functionality. They perform various high-speed operations that cannot be realized by a simple microprocessor. The primary advantage that FPGA offers is On-site programmability. Thus, it forms the ideal platform to implement and test the functional of a dedicated processor designed using CORDIC algorithm. |
| The rest of the paper is organized in the following manner. CORDIC algorithm and its operating modes are discussed in section 2. Section 3 describes the unrolled architecture of the CORDIC algorithm. Section 4 describes the result and related comparison. |
CORDIC ALGORITHM |
| The COordinate Rotation DIgital Computer (CORDIC) is known as an iterative algorithm using only shift-and-add operations to perform several mathematic functions for scientific and engineering fields. CORDIC was firstly described in 1959 by J.E. Volder [1] to evaluate trigonometric functions. In 1971, J. Walther [2] extended the CORDIC algorithm to hyperbolic functions and the algorithm is today used in many application areas such as matrix computation, digital signal processing, digital image processing, communication, robotics and graphics. The trigonometric and exponential functions that are evaluated via rotations in the circular, hyperbolic and linear coordinate systems. Their inverses can be implemented in a vectoring mode in the appropriate coordinate system. |
| Rotating a vector in a Cartesian plane by the angle θ this can be arranged so that |
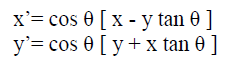 |
| If the rotation angles are restricted so that tan (θ) = ± 2-i, the multiplication by the tangent term is reduced to a simple shift operation. Arbitrary angles of rotation are obtainable by performing a series of successively smaller elementary rotations. If the decision at each iterations i, is which direction to relate rather than whether or not to rotate, then the cos(θ) term becomes a constant .The iterative rotation can now be expressed as: |
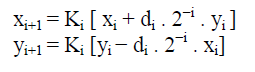 |
| Where, |
 |
| Removing the scaling constant from the iterative equations yields a shift-add algorithm for vector rotation. The product of the K can be applied elsewhere in the system or treated as part of a system processing gain or by initiating the rotating vector by the reciprocal of the gain of a certain number of iterations. The angle of a composite rotation is uniquely defined by the sequence of the directions of the elementary rotations. That sequence can be represented by a decision vector. The set of all possible decision vectors is an angular measurement system based on binary arctangents. A better conversion method uses an additional adder-subtractor that accumulates the elementary rotation angles at each single iteration. The elementary angles can be expressed in any convenient angular unit. Those angular values are supplied by a small lookup table or are hardwired, depending on the implementation. The angle accumulator adds a third difference equation to the CORDIC algorithm |
| The CORDIC rotator is normally operated in one of two modes, the rotation mode and the vectoring mode [4]. In the rotation mode, a vector (x, y) is rotated by an angle θ. The angle accumulator is initialized with the desired rotation angle θ. The rotation decision per iteration is made to diminish the magnitude of the residual angle in the angle accumulator. The decision per is therefore based on the sign of the residual angle after each step. Naturally, if the input angle is already expressed in the binary arctangent base, the angle accumulator may be eliminated. |
| For rotation mode the CORDIC equations are |
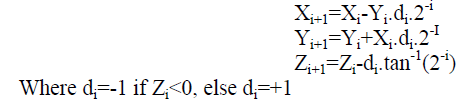 |
| After n iterations we get the following results: |
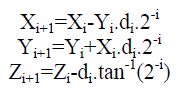 |
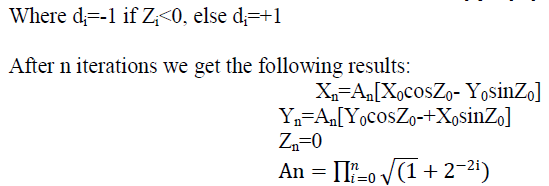 |
UNROLLED CORDIC ARCHITECTURE |
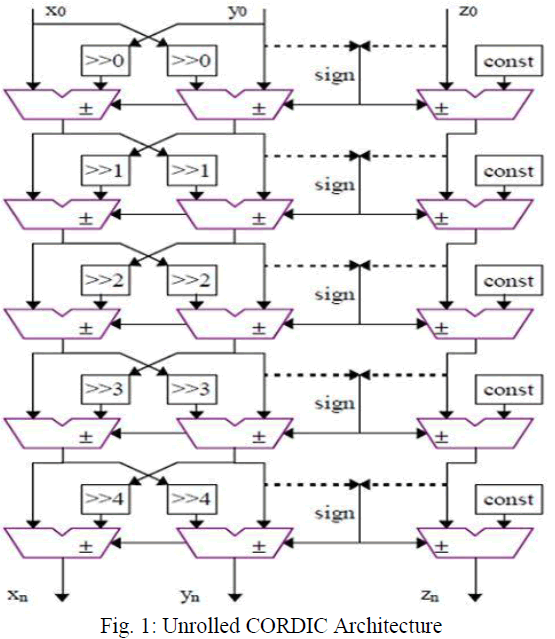 |
| An unrolled architecture is shown in fig.1.Unrolled architecture has two advantages. First one is that the shifters are of fixed size and those can be implemented in the wiring. Second, Constants can be hardwired instead of requiring storage space that is the ROM that holds the arbitrary angle values need not to be updated after every iteration. The look up table (LUT) values for computing angle accumulator is distributed as constant to each adder in the angle accumulator chain so that the entire CORDIC processor is reduced to an array of interconnected adder-subtraction units. Unlike other architectures there is no need of registers which makes the unrolled architecture strictly combinational circuit. It has considerable delay, but processing time is reduced as compared to the iterative process. So the unrolled implementation provides the speed required for faster applications |
| The various components required for the radix-2 CORDIC processor implementation in unrolled fashion are the ROM required to store the angle values tan-1(i) where i is varied from 0 to 16 and 32 for 16 bit and 32 bit processor respectively. There are barrel shifter required for shifting of the intermediate values of Xi and Yi. The barrel shifters carry out a right shift which can be implemented using multiplexers. Adder/Subtraction unit is required in each iteration to calculate the next iteration values of X, Y and Z. The counter is required for the counting of the number of iteration of the CORDIC equations. |
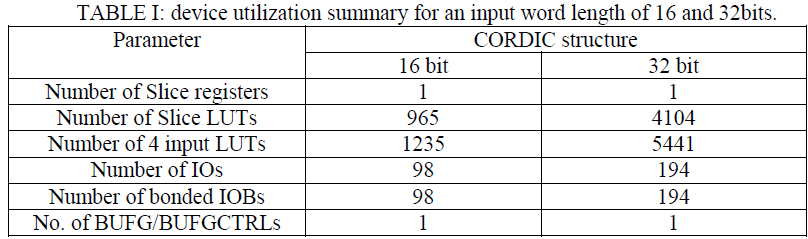
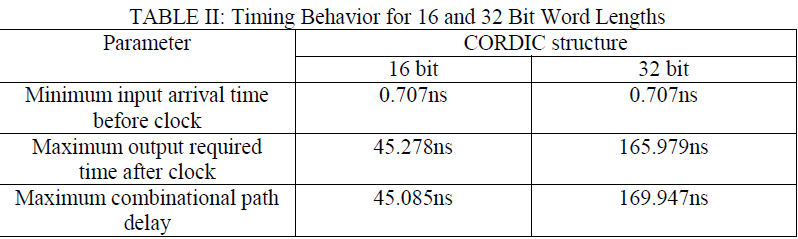
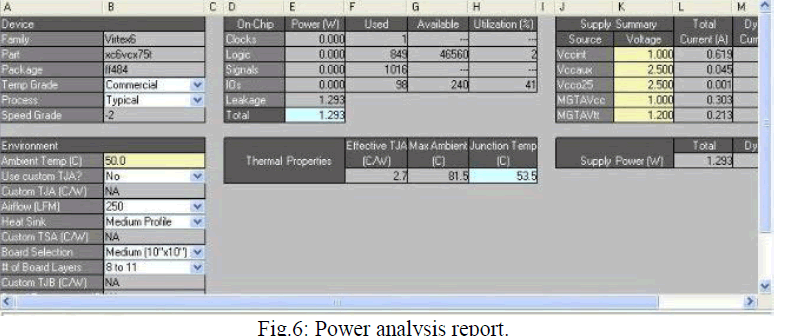
IMPLEMENTATION AND RESULTS |
| The CORDIC processor is implemented with the following synthesis description: |
| Platform: FPGA |
| Family: Vertex6 |
| Target device: XC6VCX75t |
| Package: FF484 |
| Speed grade: -2 |
| Fig. 2 and fig. 3, shows RTL schematics of the 16 & 32 bit CORDIC structure. |
 |
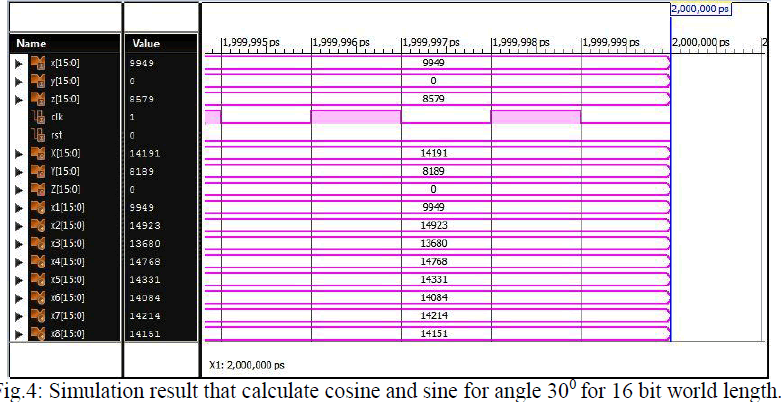
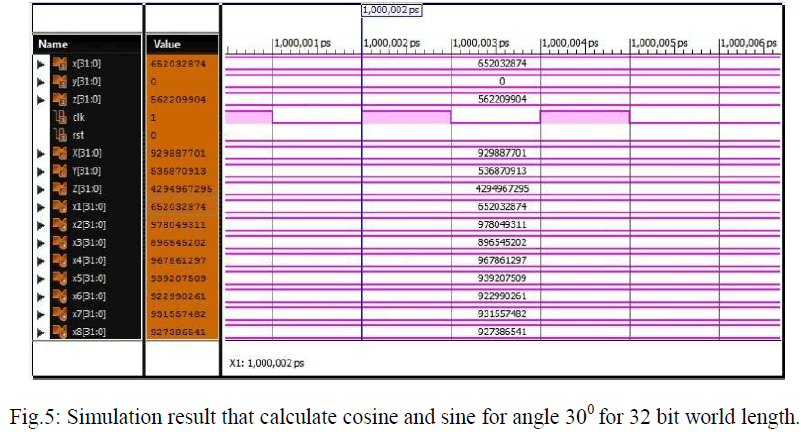
| Fig. 4 and fig.5, shows RTL simulation results of the 16 & 32 bit CORDIC structure. |
 |
 |
 |
 |
 |
CONCLUSION |
| The CORDIC is a widely used algorithm in the field of DSP applications. This affects the cost, speed and flexibility of the DSP systems. Implementation of a CORDIC based processor on FPGAs can give enhanced speed at low cost with a lot of flexibility. |
| In this project 16 and 32 bit radix-2 CORDIC architectures are designed and simulated using Xilinx ISE using VERILOG as a synthesis tool. The output of the CORDIC architectures are analysed and verified, and compared with the actual values obtained from MATLAB. It is proved that by making use of CORDIC processor we can achieve high speed operation at reduced power and resource usage, which is essential in DSP applications. The analysis was carried for radix-2 CORDIC. |
References |
|