Random Movement of particle trajectories in
a gas insulated bus duct

Swarnalatha.Nattava; J.Amaranath

Random Movement of particle trajectories in a gas insulated bus duct

Swarnalatha.Nattava¹, J.Amaranath²

Associate Professor, EEE, Swamy Vivekananda Institute of Technology, Patny Centre,Sec-Bad,AP,India.
Professor, EEE, JNT University, Hyderabad, A.P., India.

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

The present work mainly deals with the motion equation and includes the concept of random motion along axial direction by using Monte-Carlo technique. The particle moves in a random direction, this is due to the cross sectional irregularities of the particle. A method based on the particle motion is proposed to determine the particle trajectory in a Gas Insulated Bus duct (GIB). In order to compare the movement in a three-phase bus duct, appropriate equations have been derived for the field and the charge calculations. The results have been presented and analyzed for other set of parameters. The radial and axial movement are also presented in this paper.

Keywords

Axial Movement, GIB, Movement, Particle movement, Radial movement

INTRODUCTION

The various modules of GIS are factory assembled and operate with SF6 gas at pressures between 0.3 and 0.6Mpa. Such substations are compact and can be installed conveniently on any floor of a multi-storied building or in an underground substation.

A. The necessity of this study

Extremely high dielectric properties of SF6 have long been recognized. Compressed SF6 has been used as an insulating medium as well as arc quenching medium in electrical apparatus in a wide range of voltages. Due to high reliability of the equipment, Gas Insulated Substations (GIS) can be used for longer times without any periodical inspections. Conducting contamination (i.e. aluminium, copper and silver particles) could, however, seriously reduce the dielectric strength of gas-insulated system. Understanding of the dynamics of metallic particle in a coaxial electrode system is of vital importance for determining the effect of contamination in the design and operation of Gas Insulated Substation (GIS). The charge acquired by a particle, the equation of motion, the bounce and the drag, etc., are discussed by several authors. In this paper, a method based on the particle motion is also proposed to determine the particle trajectory in a three phase common enclosure GIB. Aluminum, copper and silver wires were considered to be present on enclosure surface. The motion of particle was simulated using the charge acquired by the particles, the macroscopic field at the particle site, the drag coefficient, Reynold’s number and coefficient of restitution. The motion of the particle is simulated using the parameters described above. In order to determine the movement of particle in a single phase GIB, an inner electrode radius of 55 mm and outer enclosure radius of 152 mm was considered. For the movement of the particle in a 3- Phase GIB, an outer enclosure of diameter 500 mm and inner conductors of diameters 64 mm spaced equilaterally are considered. The distance traveled by the particle, calculated using appropriate equations, is found to be in good agreement with the published work for a given set of parameters.

B. The origin of these particles

Metallic particles in GIS have their origin mainly from the manufacturing process or they may originate from moving parts of the system, such as breakers and disconnectors. They may also originate from mechanical vibrations during shipment and service or thermal contraction / expansion at joints

Metallic particles can be either free to move in the GIS or they may be stuck either to an energized electrode or to an insulator surface (spacer, bushing etc.). If a metallic particle crosses the gap and comes into contact with the inner electrode or if a metallic particle adheres to the inner conductor, the particle will act as protrusion on the surface of the electrode, and the voltage required for breakdown of the GIS will be dramatically decreased. A metallic particle stuck on an insulator surface in a GIS will also cause a significant reduction of the breakdown voltage.

The understanding of the dynamics of a metallic particle in a coaxial electrode system is of vital importance for improving the voltage withstand capacity of a Gas Insulated System. If the motion pattern of a metallic particle is generally known, the probability of a particle crossing a coaxial gap, causing a flashover, can be estimated.

METALLIC PARTICLES IN CONTACT WITH ELECTRODES

A. Modelling technique of a 1- phase GIB

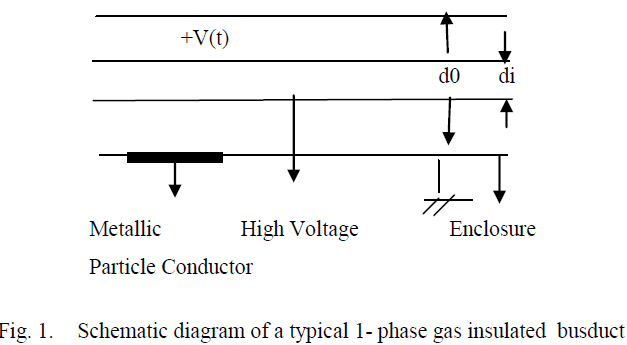In the present work the particle is on the surface of the enclosure and the enclosure is earthed. The schematic diagram of a typical compressed Gas insulated busduct is shown in Fig. (1). When the electrical field surrounding the particle is increased, an uncharged metallic particle resting on a bare electrode will gradually acquire a net charge. The charge on the particle is a function of the local electrical field and shape, orientation and size of the particle. When the electrostatic force exceeds the gravitational force the particle will lift [1-5 ]. Lift-off field for a particle can be estimated as [6-8]. In order to lift a particle from its position of rest the electrostatic force on the particle should balance its weight. Hence,

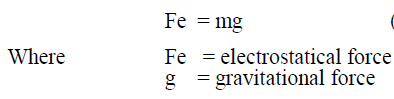Charge acquired on a horizontal wire particle :

Where, l is the wire particle length.

Lift-off field is given by [9]

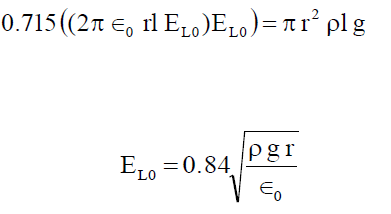Once the particle has lifted from a horizontal to a vertical position the charge will increase significantly. The sudden increase of charge will most likely lift the particle from the electrode.

Conducting particles placed in a uniform ac field lift-off at a certain voltage. As the voltage is raised, the particles assume a bouncing state reaching a height determined by the applied voltage. With a further increase in voltage, the bounce height and the corona current increase until break down occurs [9].

The work reported in this paper also deals with the movement of metallic particle in 3-phase common enclosure Gas Insulated Busduct. In order to determine the axial movement in an enclosure system, the Monte-carlo technique has been adopted in conjuction with motion equation. The distance traveled by the particle, calculated using Cartesian coordinates, for a given set of parameters is presented. In order to determine the random behaviour of moving particles, the calculation of movement in axial and radial directions was carried at every time step using rectangular random numbers.The present paper deals with the computer simulation of particle movement in 3-phase common enclosure GIB. The specific work reported deals with the charge acquired by the particle due to macroscopic field at the tip of the particle, the force exerted by the field on the particle, drag due to viscosity of the gas and random behaviour during the movement. Wire like particles of aluminium and copper of a fixed geometry in a 3-phase busduct as well as 1-phase busduct have been considered and results have been compared. The movement pattern for higher voltages class has been also obtained. Monte-carlo technique has been adopted for determining the axial movement of the particle. It has been assumed that at every time step the particle can have a maximum movement 10 to 40 from vertical.

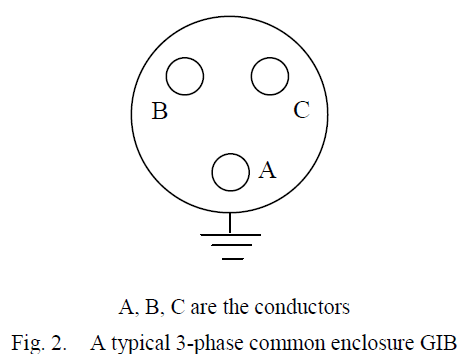
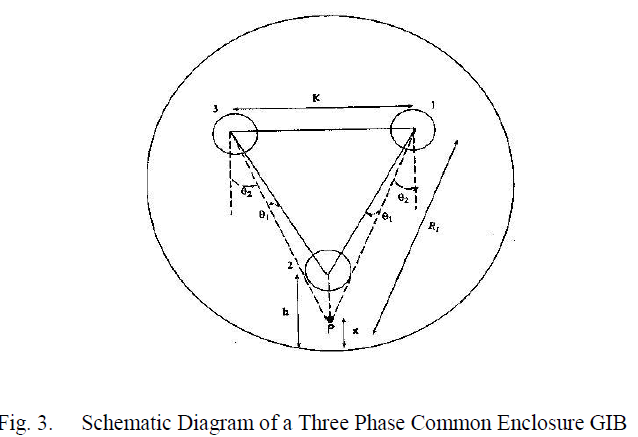
B. Modeling Technique of 3-phase GIB

The Fig. 2 and Fig. 3 show a typical horizontal three phase busduct. The enclosures are filled with SF6 gas at high pressure. A particle is assumed to be at rest at the enclosure surface, just beneath the busbar A, until a voltage sufficient enough to lift the particle and move in the field is applied. After acquiring an appropriate charge in the field, the particle lifts and begins to move in the direction of field having overcome the forces due to its own weight and air drag. The simulation considers several parameters e.g. the macroscopic field at the surface of the particle, its weight, Reynold’s number, coefficient of restitution on its impact to both enclosures and viscosity of the gas. During return flight, a new charge on the particle is assigned based on the instantaneous electric field.

C. Theoretical Study

Many authors [1-4] have suggested solutions for the motion of a sphere or a wire like metallic particle in an isolated busduct system. The theory of the particle charge and the electrostatic force on the particle is discussed elsewhere [5]. The motion equation is given by

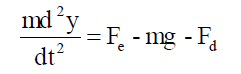Where, y is the direction of motion and Fd is the drag force. The direction of the drag force is always opposed to the direction of motion. For laminar flow the drag force component around the hemispherical ends of the particle is due to shock and skin friction. Very limited publication is available for the movement of particle in a three-phase busduct, however the equation of motion is considered to be same as that of an isolated phase busduct.

D. Simulation of electric field in 3-phase busduct

The charge acquired by the vertical and horizontal wire particles in contact with a bare enclosure and coated enclosure can be expressed as given by Srivastava and Anis [2].

The electric field in 3-phase common enclosure GIB electrode system at the position of the particle can be written as

Where, E(t) is the resultant field in vertical direction due to the field of three conductors on the surface of the particle at the enclosure. E1(t), E2(t) and E3(t) are the components of the electrical field in vertical direction. The gravitational force and drag forces are considered as described by several authors.

The motion equation is given by

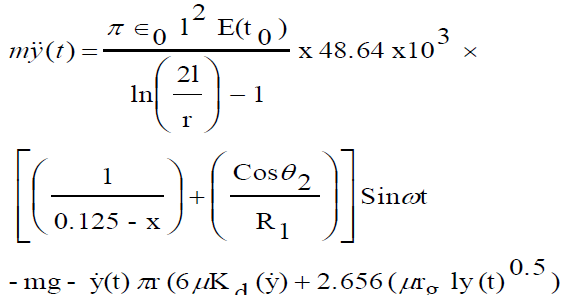Eq.7 is a non-linear second order differential equation. To obtain its solution, generally the iterative methods are to be used. The above equation is solved by using Runge-Kutta 4th order method. Simulation is done using C language.

RESULTS AND DISCUSSIONS

The study of the motion of moving metallic particles in GIS requires a good knowledge of the charge of the particle. In this simulation, the charging process of a moving particle in a single-phase isolated conductor GIB and three phase common enclosure GIB as well as the movement of particle are presented.

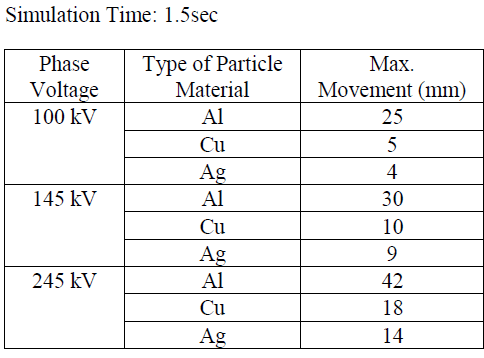
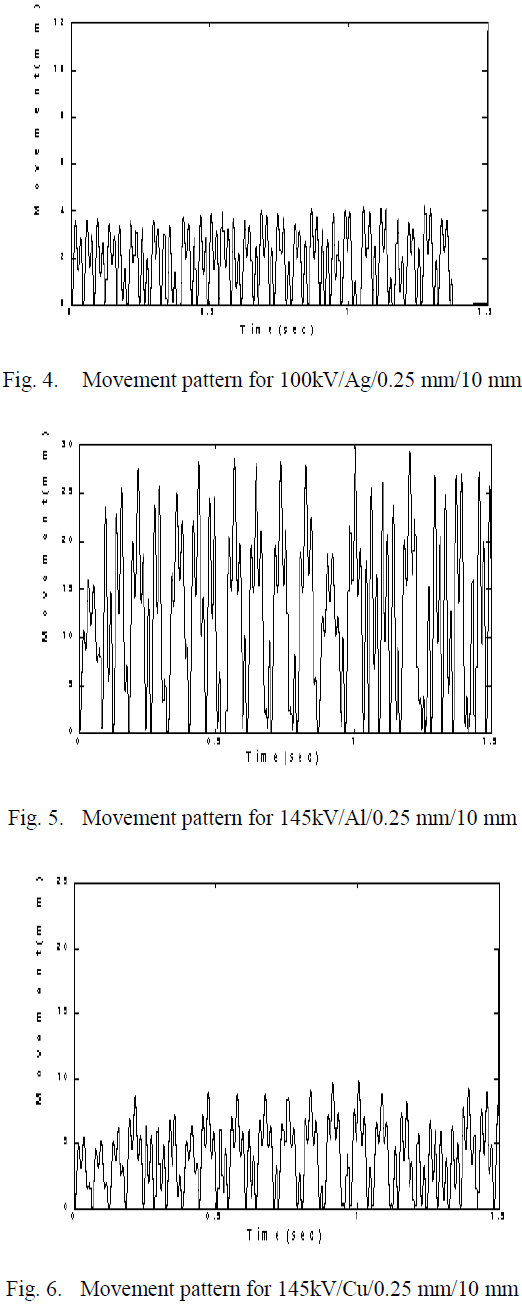
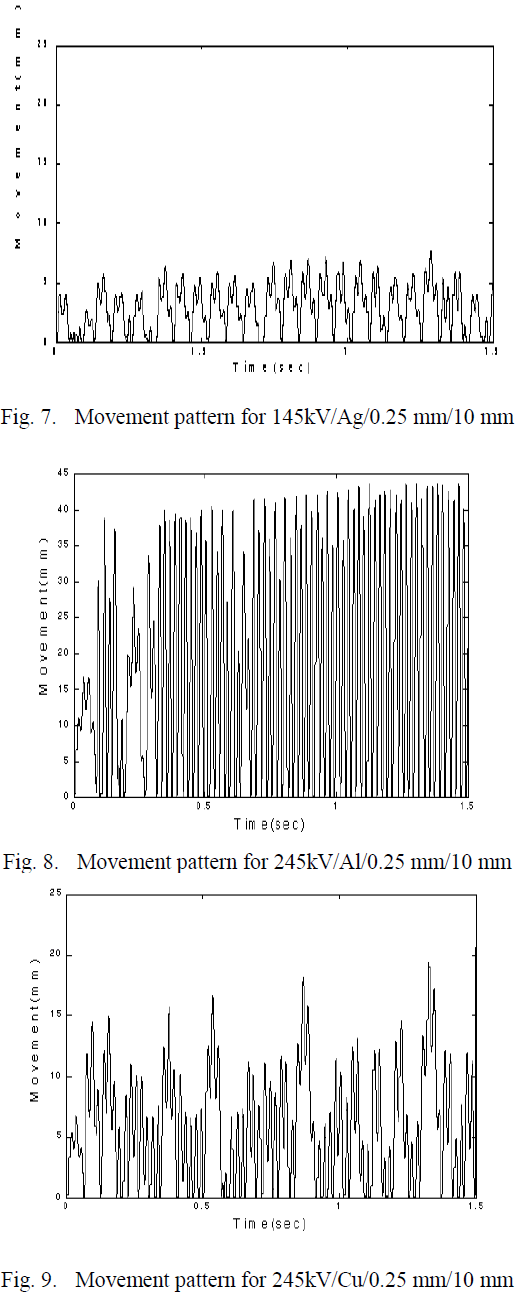
The movement of aluminium, copper and silver particles for applied voltages of 100kV, 145kV and 245kV simulation are given in table 1 Fig.4 to Fig.10 show the movement patterns of aluminium, copper and silver particles with the application of power frequency voltages.

It can be noted from Table I shows that peak movement in radial direction for aluminium particle is higher than that of copper and silver. This behaviour is expected due to heavy weight of copper and silver particles than those of aluminium of the same size. It is also observed that for a given particle and given voltage condition.

Table I

Movement (mm) of Aluminium, Copper and Silver particles with application of 100KV, 145KV and 245KV, 0.25mm radius and 10mm length

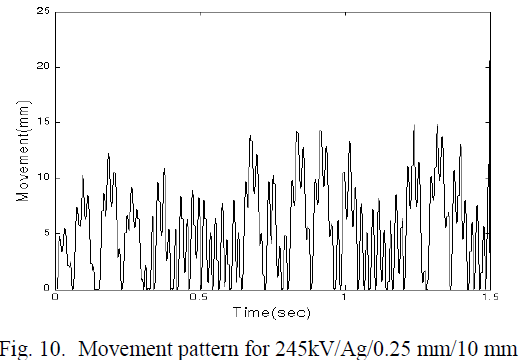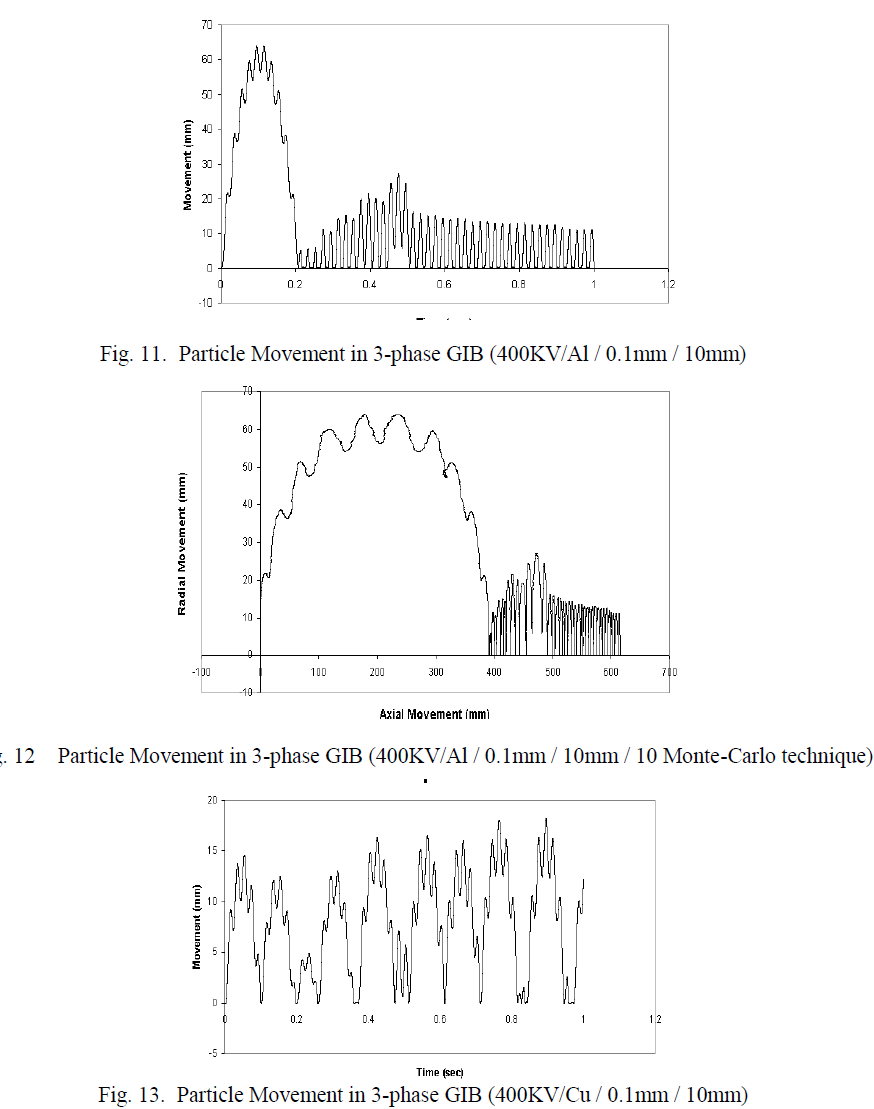
Fig. 11 shows the movement of aluminium particle in radial direction for an applied voltage of 400KV rms. During its movement it makes several impacts with the enclosure. The highest displacement in radial direction during its upward journey is simulated to be 65mm. As the applied voltage increases the maximum radial movement also increases as given in Table II. However, it is noticed that even up to a voltage of 100kv, the particle could not bridge the gap. Further calculations may reveal the limiting voltage to enable the particle to reach the high voltage conductor.

A graphical representation of radial movement in relation to axial movement is given by Monte-carlo technique as shown in Fig.12. The movement of copper particle was determined for 400kv with similar parameters as above and found to have a maximum movement of 18mm in radial direction as shown in Fig. 13. The movements are also calculated for other voltages.

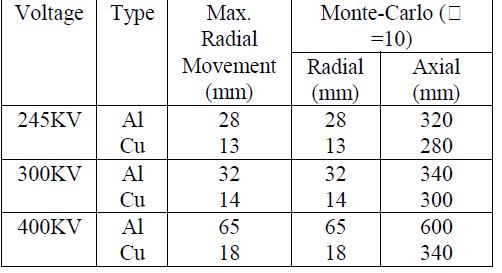
The movement of copper particle are also given in Table II. It is noticed that the movement of copper particle is far less than aluminium particle of identical size. This is expected due to higher density of copper particle. The axial and radial movement of aluminium and copper particles are calculated using Monte-carlo technique for three voltages i.e. 245kv, 300kv and 400kv with a solid angle of 10. It is significant to note that for all the cases considered, there is no change in maximum radial movement, even when Monte-carlo method is applied. A relatively high value of axial movement is achieved with the random angle of 10. As expected the axial movement of copper particle is lower than the aluminium

Table II

Axial and Radial movement of aluminium and copper particles in 3-phase common enclosure GIB

CONCLUSION

In this paper the random motion of the particle have been simulated and presented by using Monte-Carlo technique. The radial and axial movements were presented in this paper. It is observed that in a single phase isolated conductor GIB the distance traveled by the particle in a gas gap is more compared to three phase common enclosure GIB, this is due to field produced in a single phase GIB is more than the three phase GIB. By using Monte-Carlo technique the actual movement was simulated for every time step at various random angles. It is observed that for lower random angles the axial distance is less compared to higher random angles. Since the bus duct length is 2 or 3 meters it is suggested that the random angles are less than 2O will give better results than higher random angles.

ACKNOWLEDGEMENTS

The authors are thankful to managements of Swam Vivikananda Institute of Technology, Secunderabad, AP, INDIA. and JNT University, Hyderabad. AP, INDIA for financial assistance and permission to publish this work.

References

H Cookson, PC Bolin, HC Doepken, RE Wootton, CM Cooke, JG Trump; “Recent Research in the United States on the Effect of Particle Contamination Reducing the Breakdown Voltage in Compressed Gas Insulated System”; Int. Conf. On Large High Voltage System; Paris, 1976.
H.Anis, KD Srivastava; “Breakdown Characteristics of Dielectric Coated Electrodes in Sulphur Hexafluoride Gas with Particle Contamination”, Sixth International Symposium on High Voltage Engineering No. 32.06, New Orleans, LA, USA. 1989.
M.M. Morcos, S. Zhang, K.D. Srivastava, and S.M. Gubanski “Dynamics of Metallic particle contamination in GIS with dielectric coating electrodes”, IEEE Transactions on Power Delivery Vol. 15, No. 2, p.p. 455-460, April 2000.
J. Amarnath, B. P. Singh, C. Radhakrishna, S. Kamakshiah “Determination of particle trajectory in a Gas Insulated Busduct predicted by Monte-Carlo technique”, CEIDP, Texas, Austin, USA, 1999 during 17-21st October 1999.
J. Amarnath et al., “Influence of Power Frequency and Switching Impulse Voltage on Particle Movement in GIS – Predicted by Monte-Carlo Technique” International IEEE, High Voltage Workshop, Calfornia, USA, during April 18-21, 2001.
J. Amarnath et al., “Influence of Power Frequency and Impulse Voltage on Motion of Metallic particle in a coated GIS – predicted by Monte- Carlo Technique” 6th International Seminar on Electrical and Electronics Insulating Materials and Systems (IEEMA), Hyderabad, INDIA, during November 23-24, 2000.
J. Amarnath et al., “Movement of Metallic Particles in Gas Insulated Substations under the influence of various types of voltages” 11th National Power System Conference (NPSC-2000), IISc, Bangalore, INDIA during December 20-22, 2000.
J. Amarnath et al., “Effect of Various Parameters of Movement of Metallic Particles in GIS” at International Seminar on Compact Substations and Gas Insulated Switch Gears (CBIP), New Delhi, INDIA during January 19-21, 2001.
J. Amarnath et al., “Particle Trajectory in a Common Enclosure Three phase SF6 Busduct” 12th International Symposium on High Voltage Engineering, IISc, Bangalore, INDI during August 20-24, 2001.