ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| Arathy.V1, Dr.P.Srinivasa Babu2 Computer Science & Engineering, Adhiyamaan College of Engineering, Hosur, India1, 2 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Face recognition system should be able to automatically detect a face in images. This involves extraction of its features and then recognizes it, regardless of lighting, ageing, occlusion, expression, illumination and pose. Color local texture method do not easy to recognize the face and if variation in face means do not get proper results. Linear discriminant analysis (LDA) is commonly used technique for data classification and dimensionality reduction. LDA approach overcomes the above problem. The objective of LDA is to perform dimensionality reduction while preserving as much of the class discriminatory information as possible. Linear discriminant analysis is also known as fisher’s discriminant analysis and it searches for those vectors in the underlying space that best discriminate among classes
Keywords |
| Color face recognition, Color local texture features, Combination, Principal component analysis, linear discriminant analysis. |
INTRODUCTION |
| Face recognition is widely used in biometric systems. Face recognition is also useful in human computer interaction, virtual reality, database retrieval, multimedia, computer entertainment, information security e.g. operating system, medical records, online banking., biometric e.g. personal identification - passports, driver licenses , automated identity verification – border controls, law enforcement e.g. video surveillances, investigation, personal security – driver monitoring system, home video surveillance system. |
| There are different types of approaches - Appearancebased method, Feature-based approach and hybrid approach. In holistic approach the whole face region is taken into account as input data into face detection system. One of the best example of holistic methods are Eigen faces most widely used method for face recognition, In this methods local features such as eyes, nose and mouth are first extracted and their locations and local statistics (geometric and/or appearance) are fed into a structural classifier. |
| A big challenge for feature extraction methods is feature “restoration", this is when the system tries to recover features that are invisible due to large variations, e.g. head pose.There are different extraction methods, the first is generic methods based on edges, lines, and curves, the second is feature-template-based methods and the third is structural matching methods that take into consideration geometrical constraints on the features. Hybrid approach uses a combination of both holistic and feature-based approaches. Principal component analysis (PCA) is one of the most popular holistic approach i.e. appearance-based methods used for dimensionality reduction for compression and face recognition problems. Linear discriminant analysis (LDA) is another powerful dimensionality reduction technique which is also known as fisher’s discriminant analysis. It has been used widely in many applications such as face recognition, image retrieval etc.. Preprocessing procedure is very important step for facial expression recognition. The ideal output of processing is to obtain pure facial expression images, which have normalized intensity, uniform size and shape. It also should eliminate the effect of illumination and lighting. The preprocessing procedure of our system performs the following five steps: 1). detecting facial feature points manually including eyes, nose and mouth; 2). rotating to line up the eye coordinates; 3) locating and cropping the face region using a rectangle according to face model [5] as shown in Fig.1. |
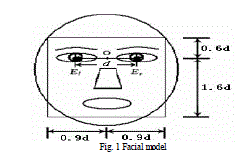 |
| Suppose the distance between two eyes is d, the rectangle will be 2.2d×1.8d; 4). Scaling the image to fixed si ze of 128×96, locating the center position of the two eyes to a fixed position; 5). Using a histogram equalization method to eliminate illumination effect. |
II. GABOR FEATURE EXTRACTION |
| The Gabor filters, whose kernels are similar to the 2D receptive field profiles of the mammalian cortical simple cells, have been considered as a very useful tool in computer vision and image analysis due to its optimal localization properties in both spatial analysis and frequency domain. |
 |
| Fig. 2 The real part of the Gabor filters with five frequencies and eight orientations for ωmax =π/2, the row corresponds to different frequency ωm, the column corresponds to different orientation θ n. In the spatial domain, a Gabor filter is a complex exponential modulated by a Gaussian function [4]. The Gabor filter can be defined as follows |
| x'=x cos θ + y sin θ, y'=-x sin θ + y cos θ |
| where (x, y) is the pixel position in the spatial domain, ω the radial center frequency, θ the orientation of Gabor filter, and σ the standard deviation of the round Gaussian function along the x- and y-axes. |
| A. GABOR FEATURE REPRESENTATION |
| The Gabor feature representation of an image I(x, y) is the convolution of the image with the Gabor filter bank ψ(x, y, ω m , θ n ) as given by: |
| Om,n(x,y)=I(x,y)*ψ(x,y,ϖm,θn) |
| where * denotes the convolution operator. The magnitude of the convolution outputs of a sample image (the first image in Fig.1) corresponding to the filter bank. |
III. PRINCIPAL COMPONENT ANALYSIS |
| Principal component analysis (PCA) is a dimensionality reduction technique which is used for compression and face recognition problems. PCA calculates the eigenvectors of the covariance matrix, and projects the original data onto a lower dimensional feature space, which is defined by eigenvectors with large Eigen values. PCA has been used in face representation and recognition where the Eigen vectors calculated are referred to as Eigen faces. PCA is a useful statistical technique that has found application in fields such as face recognition and image compression, and is a common technique for finding patterns in data of high dimension. It is one of the more successful techniques of face recognition. PCA is to reduce the dimension of the data. No data redundancy is found as components are orthogonal. With help of PCA, complexity of grouping the images can be reduced. The application of PCA is made in criminal investigation, access control for computer, online banking, post office, passport verification, medical records etc. |
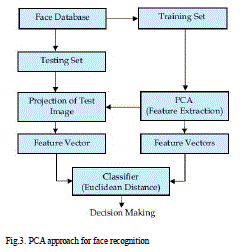 |
| Fig.3. PCA approach for face recognition METHODOLOGY: find the principal component use the following method Step1: Get the data: Suppose X1,X2,…XM is N x 1 |
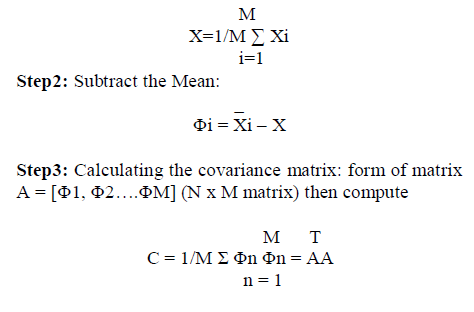 |
| Step4: Calculating the eigenvector and Eigen value of the covariance matrix. Step5: Choosing components and forming a feature vector: Once eigenvectors are found from the covariance matrix, the next step is to order them by Eigen value, highest to lowest. This gives the components in order of significance. The eigenvector with the highest Eigen value is the principle component of the data set. Choose the highest Eigen value and forming a feature vector. Step6: Deriving the new datasets: Once chosen the components (eigenvectors) that wish to keep in the data and formed a feature vector, imply take the transpose of the vector and multiply it on the left of the original data set, transposed. Final data = row feature vector * row data adjust The above formula getting the features of images, the Euclidean distance is calculated between the mean adjusted input image and the projection onto face space. The low values indicate that there is a face and display the face. |
IV. LINEAR DISCRIMINANT ANALYSIS |
| Linear discriminant analysis (LDA) is commonly used technique for data classification and dimensionality reduction. Linear discriminant analysis is also known as fisher’s discriminant analysis and it searches for those vectors in the underlying space that best discriminate among classes. The objective of LDA is to perform dimensionality reduction while preserving as much of the class discriminatory information as possible. The goal of LDA is to maximize the between-class scatter matrix measure while minimizing the within-class scatter matrix measure. |
| The PCA+LDA method, where PCA is used to project images from the original image space to the lowdimensional space and make the within-class scatter nondegenerate. However, the first dimensionality reduction using PCA can also remove the discriminant information that is useful for classification. The most efficient method was proposed, which projects the between-class scatter into the null space of the within-class scatter and chooses the eigenvectors corresponding to the largest Eigen values of the transferred between-class scatter. |
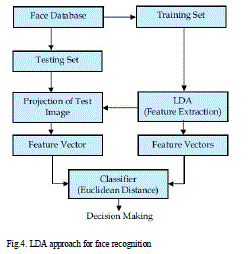 |
 |
| Step6: Calculate the mean of all classes Step7: Compute the LDA projection invSw = inv(Sw) invSw_by_SB = invSw * SB Step8: The LDA projection is then obtained as the solution of the generalized Eigen value problem Sw-1SBW = λW W = eig(Sw-1 sb) Where W is projection vector |
V. RELEVANT WORK |
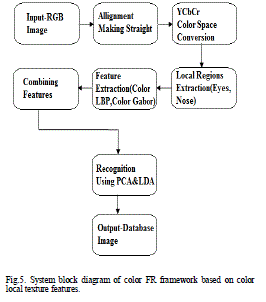
| In this section, we present a best face recognition rate for low resolution face images. The proposed modules: color space conversion and partition, feature extraction, combination and classification. a. Color space conversion and partition A face image represented in the RGB color space is first translated, rotated, and rescaled to a fixed template, yielding the corresponding aligned face image. Subsequently, the aligned RGB color image is converted into an image represented in another color space. |
| b. Feature Extraction Each of the color component images of current color model is then partitioned into local regions. Texture feature extraction is independently and separately performed on each of these local regions. Since texture features are extracted from the local face regions obtained from different color channels, they are referred to as “color local texture features. |
| c. Combination and Classification Since N color local texture features (each obtained from the associated local region and spectral channel) are available, to combine them to reach the final classification. |
 |
VI. SYSTEM PERFORMANCE |
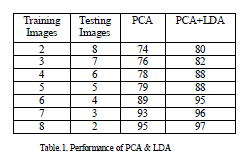
| The performances of the proposed systems are measured by varying the number of faces of each subject in the training and test faces. Table 1 shows the performances of the proposed PCA and LDA based on the Euclidean Distance classifier. The recognition performances increase due to the increase in face images in the training set. This is obvious, because more sample images can characterize the classes of the subjects better in the face space. |
 |
VII. CONCLUSION |
| In this paper, We proposed a novel local Gabor filter bank for feature extraction. A minimum distance classifier was employed to evaluate the recognition performance in different experiment conditions. The experiments suggest the following conclusions: |
| classifier was employed to evaluate the recognition performance in different experiment conditions. The experiments suggest the following conclusions: |
| 2) PCA can significantly reduce the dimensionality of the original feature without loss of much information in the sense of representation, but it may lose important information for discrimination between different classes. |
| 3) When using PCA+LDA method, the dimensionality reduced to and the recognition performance is improved. |
References |
|