Secure Computation of Face Identification (SCiFI) is a recently developed system which combines security with face recognition system and that ensures the list of faces it can identify remains private. A detailed study that shows the outcome of distorted input attacks on the system—from both a security and computer vision standpoint is given. In particular, the following is proposed, 1) a cryptographic attack that allows a fraudulent user to unnoticeably obtain a coded representation of faces on the list, and 2) a visualization approach that turns the lossy recovered codes into human-identifiable face sketches exploiting the breach.
Keywords |
| SCiFI, Reconstruction, Fragmentation. |
INTRODUCTION |
| A large research is going on computer vision is focused around facial recognition and detection. Facial
recognition is a form of biometric identification and has great application in security. In identification task to
determine if there is a close match between images, a system compares a single with list of images. This identification
process is useful especially in surveillance for identifying terrorists, criminals, or missing people from a single shot of
their face. For example, this system is useful in screening dangerous personnel from being able to board their planes in
Airport authorities. An identification system makes security camera takes images of passengers and cross-examines
them with a suspect list stored on the external server. The match of image is known by only the server and hence if any
match results then server will notify to airport authorities. The public often believes surveillance cameras or videos are
a violation of privacy. Most people do not want their day to day activities to be recorded. A compromised system links
social networking faces, an appropriate response would be to implement cryptography in the system and have data
encrypted. Even though people are still being recorded, encryption will protect the confidentiality of the individuals.
However, by introducing cryptography, scalability and efficiency are an immediate problem. Recent developed system
is Secure Computation of Face Identification (SCiFI) [1] which combines security with facial recognition. It provides
secure transmissions and facial comparisons performing face identification. SCiFI is an elegant system that allows two
mutually untrusting parties to represent and compute whether their two respective input face image matches efficiently
and securely. The SCiFI system's protocol performs a cross-examination of faces, providing no any additional
information about individual being compared or what are in the database. Hence, the suspect list is confidential and
input faces in the system are only used to check for matches. |
| We explore the outcome of dishonest user that uses distorted inputs to attack the SCiFI protocol. Our
contribution has two phases: a cryptographic attack phase and a visualization phase. In first phase we introduce an ill
formed input, an attacker knows if the particular feature exists in target image. An entire vector encoding facial parts
appearance and layout of a target person can be obtained by repeating this multiple times. Recovering facial vector
alone constitutes an attack which is not usable by a human observer, as result is scattered set of patches. In second
phase we show reconstruction of underlying face using computer vision technique. |
RELATED WORK |
| There has been a lot of work done involving human faces, such as facial recognition, modeling, and
reconstruction. We will discuss some of the relevant work and its application to our work. |
Modeling Human Faces |
| The fundamental of facial recognition is modeling human faces. We refer to Zhao and Chellappa and
references therein for more details [3]. Models class is called holistic, and the entire face representation is utilized by
these models. In facial recognition it has been shown that Eigen faces are a holistic approach [4]. Principal Component
Analysis (PCA) direct applications are Eigen faces. In face database from covariance matrix using eigenvectors face
subspace is created. Vector weights representation is done for face in the database. Now, by projecting an input face
image, into the face space we obtain weights for the particular image. An identification task is done by comparing the
input face image weights with one in face database .To perform reconstruction using face subspace we use a variation
of PCA technique. Our goal is reconstruction of human faces from a SCiFI facial vector by using PCA to estimate
regions of missing facial information in contrast to classic Eigen faces technique. Active Shape Models (ASM) [5] and
their extensions, Flexible Appearance Models (FSM) [6] and Active Appearance Models (AAM)[7] are more advanced
than Eigen faces. ASM introduce idea of analysis through synthesis, they are much more flexible and robust than Eigen
faces. In addition to shape both FSM and AAM try to account for textural variations. The idea of splitting into two
separate components appearance and spatial is utilized by SCiFI. |
| 3-D Morphable models are powerful in modeling area. The 3-D faces from photographs are generated by these
models [8]. We also want reconstruct a very natural human face from our extracted facial vector. However, our face
must resemble the true face. The SCiFI system uses a part-based model to form an index-based face representation. A
part-based model gives the representation of faces as collection of images or fragments corresponding to different parts
of the face. Face can be turned easily into index based models if parts are fixed, because these models split up the
representation of the face into different parts. For face recognition using boosting and transduction Li and Wechsler
used part-based models [9].To fool an identification system they proposed the idea of an impostor to hide or occlude
parts of his/her face. However, certain parts of the face that will remain unchanged, and such parts can be utilized for
successful identification. As the SCiFI system is aimed to be used in security, this process helps in motivating the usage
of a part-based model. A pictorial structure representations using one form of part-based models have been shown for
facial recognition[10].To detect faces and human bodies in novel images pictorial structures can be used [11].However,
the facial encoding does not provide the optimal way of combining the appearance and spatial information to form a
patch face ,our work appearance and spatial information is encoded inside the facial vectors. |
Secure Facial Recognition |
| Facial recognition is a large area of study in computer vision and is a very successful area in image analysis.
Actually, there are three tasks (1) detection, (2) feature extraction, and (3) identification and/or verification [3]. There
are two major problems that arise while combining security with facial recognition is a difficult. The facial recognition
systems want to match similar inputs, for no two images of a face are going to be exactly the same is the first problem.
Since cryptographic algorithms require two inputs to be exactly the same, this is a problem of cryptography. Thus,
some works introduce the idea of “fuzzy" schemes attempting to solve this problem [12, 13]. Now, given similar image
inputs, one can map them to the same result. |
| The current state-of-the-art facial recognition algorithms often employ continuous representations of faces is a
problem. This is a problem for cryptographic algorithms that utilize discrete values. Conversion to discrete one from a
continuous representation will affect facial recognition accuracy. Utilizing Eigen faces work has been done with secure
facial recognition [14,15]. For enabling Cryptography to be applied to facial representations, the Eigen faces are
essentially quantized. They require large amounts of computation to query the system for face matches even when these
systems have been shown to be effective in securely recognizing faces. The usage of Eigen faces implies that every
pixel must be used, and with higher image resolutions, there is a facial recognition accuracy and time complexity trade off. In addition, a simple match detection by comparing the Hamming distance of two face vectors is allowed by
SCiFi’s facial representation. In our work, we reverse engineer face images by utilizing this representation. |
Reconstructing Occluded Regions of Faces |
| Facial occlusions are one major problem that face recognition systems encounters. The range can vary from
glasses, hair, or even some external object blocking a part of a person's face. Thus, how to remove occlusions or work
around them is an interesting problem in computer vision. We can treat missing regions of a person's face as being
damaged or occluded in our task. A fair amount of work is done dealing with removing occlusions. The work has been
done on removing eyeglasses from facial images [16].Firstly they isolate the region and then use recursive PCA to
synthesize the eyes of the face based on the surrounding information without glasses. This process is very similar to
how we will perform our face reconstruction. PCA on a morphable face model has also been investigated [17]. One
drawback with this approach is the lack of precision of the displacement between the input face and the reference face.
There are other similar techniques using PCA for reconstruction [18, 19, 20].The previously done reconstruction
techniques have been fairly successful. In our case the source is a fragmented reconstruction itself, computed from a
fairly course binary face encoding however, whereas in all previous such methods a real image is the true source. In
addition, our reconstructions are estimating 60%-80% of missing facial information as opposed to very specific and
small occluded regions such as where eyeglasses lie. These two issues make our reconstruction task significantly more
challenging. In addition, our task of sketching faces based on a security break is novel, and has compelling practical
implications. |
FRAMEWORK: THE SCiFI SYSTEM |
| The brief overview of the SCiFI system [1]. The SCiFI system server stores a list of faces and the client inputs
a single face into the system. The system goal is to securely test whether the face input by the client is present in the
server's list. The typical setting has the server's list comprised of faces of suspects or criminals, while the client inputs a
face of a passerby from a surveillance camera. To this end, SCiFI develops a part-based face representation, a robust
distance to compare two faces, and a secure client-server protocol to check for a match according to that distance, as we
explain next. |
Face Representation: In order to perform the secure computation, in SCiFI system each face is deconstructed into a
standard set of facial features(nose,mouth,eyes).The system establishes a set of typical examples of that feature based
on an unrelated public database Y for each feature. The most similar word to input face feature is selected from the
appearance vocabulary 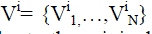 and arranging these words in a spatial configuration similar to the input will
produce an output similar to the original face.The representation also keeps track of the distance of each input feature
from the center of the face to match the spatial configuration called spatial vocabulary 
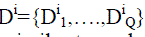Thus, the final
face representation is comprised of the set of features in the vocabulary that are most similar to each feature, and the
approximate distance of each feature from the center of the face. |
For input face, let the set of its patches be {I1,…,Ip}.For each Ii two things are recorded :Appearance
component, it contains the indices of n visual words in Vi that are similar to Ii, set 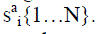 .Spatial component ,it
contains the indices of the z distance words in Di which are closest to Ii’s distance from the center of the face, set ss
i
{i…,Q}. |
| Comparing Faces: To compare two faces, SCiFi uses distance metric to decide whether two faces match. The SCiFi
system considers faces to be matched if the distance metric is below certain threshold value. |
As shown in [20], Hamming distance is set difference if the sets are coded as l=p(N+Q)-bit binary vectors. Each set sa
i
is represented by wa
i,N-bit binary indicator vector for which n entries are 1(i.e., those n indices that are in sa
i).Similarly,
each set ss
i is represented by ws
i,a Q-bit binary indicator vector for which z entries are 1.The full representation for a
given face is  |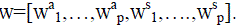
| Secure Protocol: SCiFi protocol input is a list of M face vectors w1,…wM thresholds t1,…tM from the server, single face
vector w from the client. The protocol’s output is “match”, if H (wi,w)<ti for some i,and “no match” otherwise where H
is Hamming distance. |
CRYPTOGRAPHIC MALFORMED INPUT ATTACK |
| The proposed attack on SCiFI allows the attacker to obtain a face code (w) that was meant to remain private.
The attack relies on the fact that a dishonest adversary is able to input vectors of any form, not just vectors that are
properly formatted. The attack learns the client’s face code bit-by bit through the output of “match” or “no match”. |
| Suppose the client’s vector is w. A dishonest server can add any vector wm to its suspect list, and choose each
corresponding threshold value, tm, arbitrarily. First, the server inputs the vector wm = [1, 0, . . . , 0], with a 1 in the first
position and zero everywhere else. Next, the protocol comparing w and wm is run as usual.By learning whether a
match was detected, the server actually learns information about the first bit, w1, of the client’s input. We know that the
nonzero entries of the input client vector must sum to exactly p(n+z). This creates two distinct possibilities in the
outcome of the protocol: |
| • w1 = 1: In this case, the two input vectors will not differ in the first position. Therefore, they will only differ in
the remaining p(n + z) − 1 positions where w is nonzero. Hence, we know that the Hamming distance between the two
vectors is H (w,wm) = p(n+z)−1. |
| • w1 = 0: In this case, the two input vectors will differ in the first position. In addition, they will differ in all of
the p(n + z) remaining places where w is nonzero. Hence, we know the H (w,wm) = p(n + z) + 1. |
| Taking advantage of these two possible outcomes, the dishonest server can fix the threshold tm = p(n+z).
Then, if a match is found, it must be the case that H (w,wm) =p(n + z) – 1 ≤ p(n + z), so w1 = 1. If a match is not found,
then H (w,wm) = p(n + z) + 1 > p(n + z), so w1 = 0. Thus, the dishonest server can learn the first bit of the client’s
input. Consequently, the attacker can learn the client’s entire vector by creating l vectors wi
m , 1≤ i≤ l, where the i-th
bit is set to 1. |
PROPOSED SYSTEM |
| Our method consists of two major components. The first is the offline stage that builds the facial vocabulary and face
subspace from the public database. The second is the online stage that assembles a human face and is done only after a
face vector is obtained. |
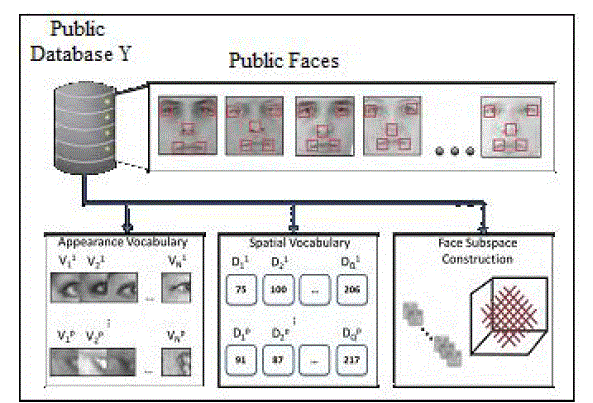
| Offline Stage: The face images should come from an external database Y, which are used to create the fragment
vocabularies which can be completely unrelated to the people registered in the server's list. All faces are normalized to
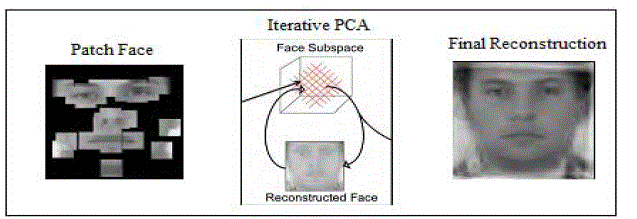
a canonical size, and the positions of landmark features (i.e., corners of the eyes) are assumed to be given. Figure 5.1
gives idea about what is done in offline stage. |
| Given face images in external database, to form appearance and spatial vocabularies V1,…Vp and D1,..Dp use
an unsupervised clustering algorithm (k-means) to quantize image patches and distances.We also use the external
database Y to construct a generic face subspace. The space of all face images occupies a lower-dimensional subspace
within the space of all images, as has been long known in the face recognition community[21,17].To compute lowdimensional
image representations this face can be exploited. In order to “hallucinate” the portions of a reconstructed
face not covered by any of the p patches we exploit a face subspace. |
Formally, face images in external database Y consist of a set of F vectors 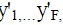 where each y'i is
concatenating the pixel intensities in each row of the i-th image. By computing mean face 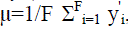 and then
center original faces by subtracting the mean from each one. |
Let the matrix Y contain those centered face instances, where each column is an instance  |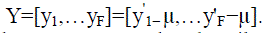
Principal component analysis (PCA) identifies the ordered set of F orthonormal vectors u1,…uF that describes
the data, by capturing the directions with maximal variance. The eigenvectors of 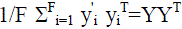 ,sorted by the
magnitude of their associated eigenvalues,by the definition the desired vectors are the eigenvectors of the covariance
matrix computed on Y.The top K eigenvectors define a K-dimensional face subspace. |
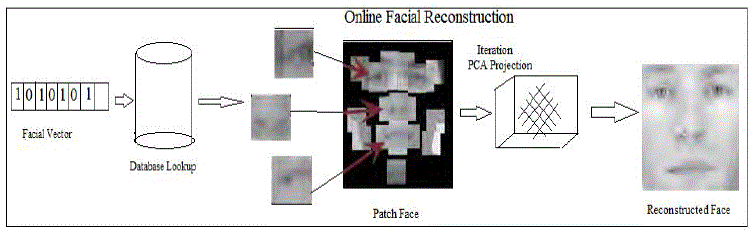
| Online stage: The SCiFI protocol can be executed after building appearance and spatial vocabularies. A patch face
representing the individual using the indices from the vector will be shown by attackers by reverse engineering. The
attacker can estimate the missing regions of the face and return a identifiable human face using our reconstruction
technique. Figure 5.2 provides an outline of the second stage of our visual reconstruction. |
| Finding a best matching face: Now we can define how to form patch face reconstruction. For each face of p facial parts,
the cryptographic attack defined above yields the n selected appearance vocabulary words and z selected distance
words. This encoding reveals which prototypical appearance and spatial was most similar to those that occurred in the
original face specifying indices into public vocabularies. |
| Thus, we map retrieved corresponding quantized patches and distance values for each part into an image
buffer. we take the n quantized patches and randomly select one of them to reconstruct the appearance of a part i . We
average the z distance values for spatial information of part i. We place the patch into the buffer relative to its center,
displaced according to the direction oi and the amount given by the recovered quantized distance bin. For example, if n
= 4 and sa
i={1,3,7,19},we look into the patches {vi
1,vi
3,vi
7,vi
19},and compute average then,if say z=2,and he associated
distances are ss
i={4,10},we average patch’s center at ½(Di
4+Di
10)oi, where the buffer’s center is at the origin. To get the
patch face reconstruction we repeat this for i=1,…, p.Figure5.3 shows an example patch face. To reverse the SCiFi
mapping the process uses all information available in encoding. |
| Principal component analysis: Based on Face Reconstruction |
| The remainder of the face image based on the constraints given by the initial patch face is estimated by second
stage of our reconstruction approach .We can exploit the structure in the generic face subspace to hypothesize or
estimate values for the remaining pixels because these regions are outside of the original SCiFI representation.
Associated uses of subspace methods have been investigated for dealing with partially occluded images in face
recognition for example, to reconstruct a person wearing sunglasses, a hood, or some other strong occlusion before
performing recognition [16, 18, 19, 17, 20]. Here we want to reconstruct portions of the face that are missing, with the
end goal of creating a better visualization for a human observer or a machine recognition system. |
| We adopt a recursive PCA technique presented in [20], which is used to compensate for an occluded eye
region within an otherwise complete facial image. Firstly we will initialize the result with our patch face, and then
project iteratively into and using public face subspace reconstruction is done each time adjusting the face with our
known patches. Comparable to experiments in [20], our process makes substantially greater demands on the
hallucination, since about 60%-80% of the total face area has no information and must be estimated. Figure 5.4 gives a
sketch of this technique. |
| Given a novel face x, to obtain its lower-dimensional coordinates in the face space we project face onto the top
K eigenvectors (so called eigen faces). Particularly, the i-th Projection coordinate is: |
 |
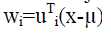| For i=1,…, K.The resulting w= [w1,w2,….,wk] weight vector specifies the linear combination of eigenfaces that best
approximates (reconstructs) the original input: |
 |
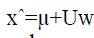| Where the i-th column of matrix U is ui. In our case simply reconstructing once from the lower dimensional coordinates
may give a poor hallucination, since many of the pixels have unknown values (and are thus initialized at an arbitrary
value of 0). |
| However, by bootstrapping the full face estimate given by the initial reconstruction with the high-quality patch
estimates, we can continually refine the estimate using the face space. This works as follows: Let x0 denote the original
patch face reconstruction. Then, define the projection at iteration t as |
 |
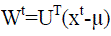| the intermediate reconstruction at iteration t + 1 as |
 |
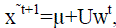| and the final reconstruction at iteration t + 1 as |
 |
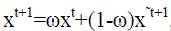Where the weighting term ω is a binary mask the same size of the image that is 0 in any positions not covered by an
estimate from the original patch face reconstruction, and 1 in the rest. We cycle between these steps, stopping once the
difference in the successive projection coefficients is less than a threshold: max  |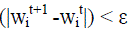
EXPERIMENTAL RESULTS |
| This experimental results figure 5.5 shows the triplet from left to right original image, patch face and
reconstructed image. When the input image is sent its features are extracted and stored in database .In general all public
faces images and their extracted features are stored in SCiFI system if matching features are found to input face image
then patch face image is formed and applying PCA algorithm to it we finally get a reconstructed face image which
resembles the original face image. We apply PCA iteratively after patch face is to get a reconstructed face. We see that
reconstructed faces forms the sketches of true face which are underlying. |
CONCLUSION |
| We present a novel attack on a secure face identification system that control detailed perception from both
security as well as computer vision techniques. While the SCiFI system appropriately claims security only under the
honest but-curious model, we have demonstrated the dangerous consequences of such a system when exposed to a
dishonest adversary. Our vision contributions are to stretch the limits of subspace-based reconstruction algorithms for
visualization of severely occluded faces. |
| |
Figures at a glance |
 |
 |
 |
 |
 |
| Figure 5.1 |
Figure 5.2 |
Figure 5.3 |
Figure 5.4 |
Figure 5.5 |
|
| |
References |
- M. Osadchy, B. Pinkas, A. Jarrous, and B. Moskovich, ″SciFI - a system for secure face identification," in IEEE Symposium on Security and Privacy, 2010.
- M. Gerbush, A. Luong, B. Waters, and K. Grauman, ″Reversing SCiFI: The dangers of malicious adversaries," Manuscript, 2010.
- W. Zhao, R. Chellappa, P. Phillips, and A. Rosenfeld, ″Face recognition: A literature survey," Acm Computing Surveys (CSUR), 2003.
- M. A. Turk and A. P. Pentland, ″Face recognition using eigenfaces," in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Hawai, Jun. 1992.
- T. Cootes, C. Taylor, D. Cooper, J. Graham, and A. Lanitis, ″Active shape models," Computer Vision and Image Understanding 1995.
- A. Lanitis, C. Taylor, and T. Cootes, ″Automatic interpretation and coding of face images using flexible models," Pattern Analysis and Machine Intelligence, IEEE Trans-actions 1997.
- T. F. Cootes, G. J. Edwards, and C. J. Taylor, ″Active appearance models," in Proceedings of European Conference on Computer Vision, vol. 1407, 1998.
- V. Blanz and T. Vetter, ″A morphable model for the synthesis of 3D faces," in Proceedings of the 26th annual conference on Computer graphics and interactive techniques.ACM Press/Addison-Wesley Publishing Co., 1999.
- F. Li and H. Wechsler, ″Robust part-based face recognition using boosting and transduction," in BTAS07, 2007.
- M. Fischler and R. Elschlager, ″The representation and matching of pictorial structures," Computers, IEEE Transactions on, vol .100 1973.
- P. Felzenszwalb and D. Huttenlocher, ″Pictorial structures for object recognition," International Journal of Computer Vision, vol. 61, 2005.
- A. Juels and M. Wattenberg, ″A fuzzy commitment scheme," in Proceedings of the 6th ACM conference on Computer and communications security. ACM, 1999.
- A. Juels and M. Sudan, ″A fuzzy vault scheme," Designs, Codes and Cryptography, 2006.
- Z. Erkin, M. Franz, J. Guajardo, S. Katzenbeisser, I. Lagendijk, and T. Toft, ″Privacy preserving face recognition," in Privacy Enhancing Technologies. Springer, 2009.
- A. Sadeghi, T. Schneider, and I. Wehrenberg, ″Efficient privacy-preserving face recognition″,Information, Security and Cryptology 2010.
- C. Du and G. Su, ″Eyeglasses removal from facial images," Pattern Recognition Letters, 2005.
- B.-W. Hwang and S.-W. Lee, ″Reconstruction of partially damaged face images based on morphable face model," IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), vol. 25, no. 3, 2003.
- A. Lanitis, ″Person identification from heavily occluded face images," in ACM Symposium on Applied Computing, 2004.
- Y. Saito, Y. Kenmochi, and K. Kotani, ″Estimation of eyeglassless facial images using principal component analysis," in International Conference on Image Processing, 1999.
- Z.-M. Wang and J.-H. Tao, ″Reconstruction of partially occluded face by fast recursive pca," Computational Intelligence and Security Workshops, International Conference on, 2007.
- P. Viola and M. Jones, ″Rapid object detection using a boosted cascade of simple features," 2001
|
Menu