Recovery Service Policy in Railway System
during Disruption

Alok Saxena; B.K.Singh

Recovery Service Policy in Railway System during Disruption

Alok Saxena¹, B.K.Singh²

Assistant Professor, Department of Mathematics, Moradabad Institute of Technology, Moradabad, Uttar Pradesh, India
Professor& Head, Department of Mathematics, IFTM University, Moradabad, Uttar Pradesh, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper is based on the decisions on recovery services for short-term disruptions during emergencies in railways system. The basis is to examine whether the railway management should collaborate with a local bus provider to provide the recovery service and how to price to compensate the service. The average arrival time of bus which is the leading decision variable, is formulated and analyzed. Both theoretical and numerical sensitivity analyses are measured to discuss the critical factors affecting the decisions.

Keywords

Transport systems, Disruption, Recovery service, Railway systems, Optimization

INTRODUCTION

Developing better solution for train rescheduling problems is drawing the attention of researchers for decades. Railway authorities aim to provide transportation services to their customers in a safe as well as effective and efficient manner but the railway system always faces disruptions caused by unexpected events such as track misalignment, power failure and natural disasters etc., which result in inconvenience to passengers and reduction of the desired service levels. Therefore, it is important to have an effective disruption handling procedure to provide high-quality passenger service.

The challenge is to respond to short-term, unplanned disruptions that require real-time and fast recovery decisions especially for passenger trains in India. When such a short-term disruption occurs, how should the railway system react? – should it wait till the problem is solved and let the passengers wait or find their own transport alternatives, or offer a temporary recovery service to the impacted passengers?

This turns out that railway system in many countries has attempted to apply similar strategies for un-planned short-term disruptions in the past. As, they use their own buses to provide temporary service to the passengers. Their other alternative is to hire buses from a local bus provider to ensure faster rail replacement service to minimize customer inconvenience. As, buses can easily arrive on the spot and are a perfect solution for replacement in the beginning. Through temporary bus service for recovery the railway system expect a reduced recovery time. In addition, it also relieves the pressure of railway system’s control centres, as the arrangement of the buses is conducted by the local bus provider. This gives ample time to concentrate on recovering the system.

The recovery method: Buses will be ordered only for the longer duration of the disruption. The railway management order a required number of buses. The buses will immediately arrive at the affected station and then take the passengers to the next station or any nearby bus or subway station, without deviating the route. Service charges to the bus provider will be paid by the railway. Passengers will be advised not to call the transport on their own; otherwise they would have to pay for the service.

II. RELATED LITERATURE

Firstly Clausen, J., Larsen, J., Larsen, A., Hansen, J., (2001) presented a theory on disruption management between planning and execution. In the same year Bertsimas, D., Perakis, G., (2001) proposed a dynamic pricing approach. Kachani, S., Perakis, G., (2002) discussed a fluid model of dynamic pricing and inventory management for make-tostock manufacturing systems. Bichler, M., Kalagnanam, J., Katircioglu, K., King, A.J., Lawrence, R.D., Lee, H.S., Lin, G.Y., Lu, Y., (2002) share the applications of flexible pricing in business-to-business electronic commerce. Schade, J., Schlag, B., (2003) coded the acceptability of urban transport pricing strategies. Perakis, G., Sood, A., (2004) focused on competitive Multi-period Pricing with Fixed Inventories. Klahn, V., (2004) discuss the effective management of reduced track capacity caused by maintenance possessions can minimize disruption to passengers and offer practical transport alternatives. Freling, R., Lentink, R.M., Waglmans, A.P.M., (2004) present a decision support system for crew planning in passenger transportation using a flexible branch-and-price algorithm. Clausen, J., (2007) proposed a disruption management in passenger transportation—from air to tracks. D’Ariano, A., Pranzo, M., (2009) presented an advanced real-time train dispatching system for minimizing the propagation of delays in a dispatching area under severe disturbances. Corman, F., D’Ariano, A., Pacciarelli, D., Pranzo, M., (2010) showed a tabu search algorithm for rerouting trains during rail operations. Jia, J., Hu, Q., (2011) discuss a dynamic ordering and pricing for a perishable goods supply chain.

III. NOTATION AND ASSUMPTIONS

In the decision-making process, time is a critical factor. There are three time related parameters in this paper. The first two input parameters whose values can be calculated at the time of disruption are as follows:

1. The average duration of a disruption td and

2. ts is the average time of round-trip for each bus.

3. The last parameter tc , is the average time it takes for the buses to arrive at the disruption site, and is treated as a decision variable for the local bus provider.

Clearly, tc affects the railways recovery service payment, which in turn impacts the railways additional profit. To proceed with our modeling process, we make the following assumption:

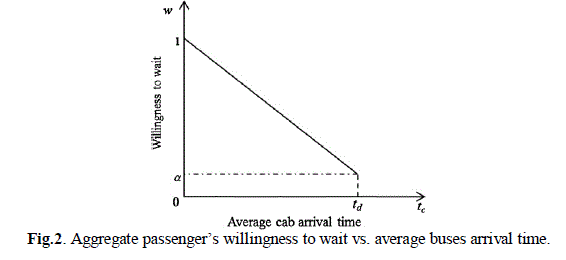
1. Aggregate passenger’s behaviour is assumed instead of each one. The aggregate passenger’s willingness to wait, w(tc), is supposed to decrease linearly as the bus’s arrival time (tc) increases and can be calculated from equation (1). Fig. 2 shows the relationship between the willingness to wait and the average bus’s arrival time. This assumption includes the fact that if buses arrive instantaneously, then all the passengers will stay to use the service; and if bus’s arrival time is about the same as the duration of the disruption, then only a small portion of passengers will wait for the service.

We consider two pricing methods to pay the local bus provider:

(i) Fixed payment with p0 being the constant unit time payment; and

(ii) Linear pricing with the payment rate decreasing linearly with the bus’s arrival time (tc), shown in the Fig. 3. This pricing scheme is defined by a pair of parameters, (pm, β).

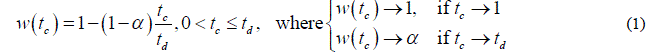IV. MODELS AND ANALYSES

then the railway should consider working with the bus provider to provide a recovery service. The condition in (14) indicates a upper bound of the unit passenger loss as

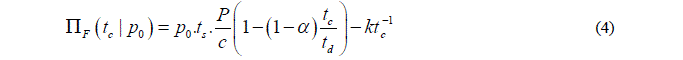VI. SENSITIVITY ANALYSIS

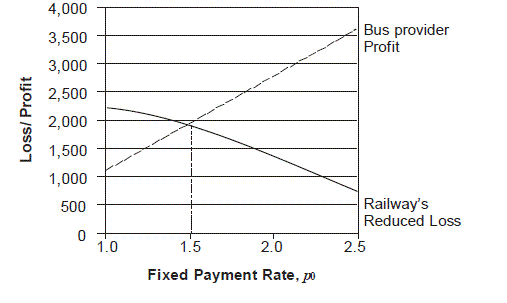
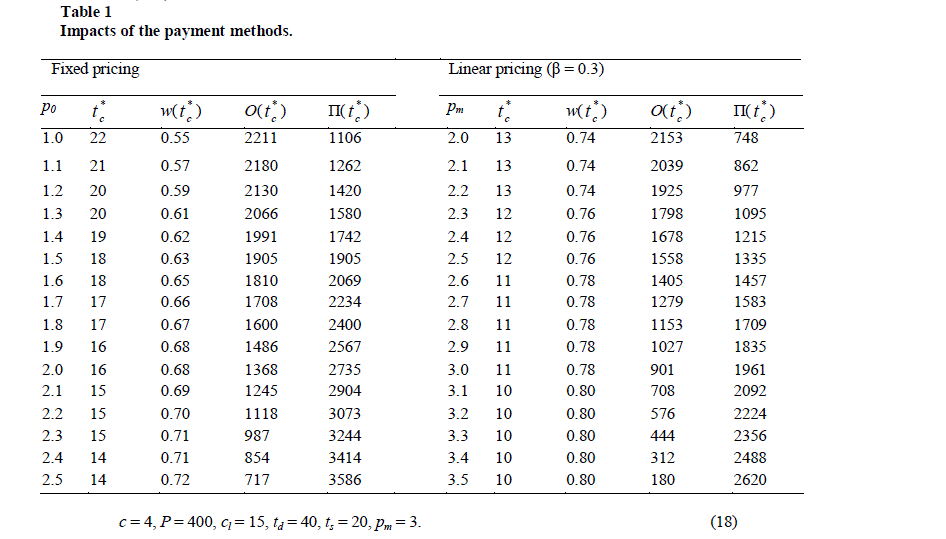
To understand the impacts of the input parameters on the two parties’ decisions, namely the optimal average arrival time tc, and the railways pricing scheme, we conduct a series of numerical experiments. The base values of the input parameters based on the real-world situations are chosen as follows:

VII. CONCLUSION

Thus, the major contributions of this research contain two main steps: first step was to formulate the decision-making situation and to decide whether to collaborate with a second party for the recovery service whereas, second step was to decide how to compensate the recovery service so that the majority of the passengers affected by the disruption can be benefitted from the recovery arrangement. As a result, two sets of mathematical models are developed and analyzed, and a series of hypothetical numerical and sensitivity studies is conducted. Finally and essentially to balance the two dimensions: the passengers’ satisfaction and the recovery cost, the railways should prefer the fixed pricing method for the passengers’ satisfaction in spite of the few limitations in the mathematical models so that the short –term disruptions may be avoided during emergencies especially for the passenger trains.

So, particularly the well-known concept in supply chain management namely, the supply contract can be introduced to disruption recovery planning in railway systems as opportunities for future research are plentiful in the same field.

References

Bertsimas, D., Perakis, G., “Dynamic Pricing: A Learning Approach”, Working Paper, Operations Research Center, OR 355-01, 2001.
Clausen, J., Larsen, J., Larsen, A., Hansen, J., “Disruption management operations research between planning and execution”, OR/MS Today 28 (5), pp.40– 43, 2001.
Bichler, M., Kalagnanam, J., Katircioglu, K., King, A.J., Lawrence, R.D., Lee, H.S., Lin, G.Y., Lu, Y., “Applications of flexible pricing in business-to-business electronic commerce”, IBM Systems Journal, vol.41, No.2, pp.287–302, 2002.
Kachani, S., Perakis, G., “A Fluid Model OF Dynamic Pricing and Inventory Management for Make-to-stock Manufacturing Systems”, Working Paper, Operations Research Center, OR 362-02, 2002.
Schade, J., Schlag, B., “Acceptability of urban transport pricing strategies”, Transportation Research Part F, vol.6, No.1, pp.45–61, 2003.
Freling, R., Lentink, R.M., Waglmans, A.P.M., “A decision support system for crew planning in passenger transportation using a flexible branchand- price algorithm”, Annals of Operations Research, vol.127, No.1 pp.203–222, 2004.
Yu, G., Qi, X., “Disruption Management”, World Scientific Publishing Co. Pte. Ltd., Singapore, 2004.
Klahn, V., “Planning maintenance site timetables: effective management of reduced track capacity caused by maintenance possessions can minimize disruption to passengers and offer practical transport alternatives”, International Railway Journal and Rapid Transit Review, vol.44, no.3, 42, 2004.
Perakis, G., Sood, A., “Competitive Multi-period Pricing with Fixed Inventories”, Working Paper, High Performance Computation for Engineered Systems (HPCES) ,2004.
Clausen, J., “Disruption management in passenger transportation—from air to tracks”, In: 7th Workshop on Algorithmic Approaches for Transportation Modeling, Optimization and Systems, Sevilla, Spain, 15–16, November 2007, pp. 30–47, 2007.
Garcia, R., Almodovar, M., Parreno, F., “Heuristic algorithm for coordination in public transport under disruptions: applications of evolutionary computing”, Lecture Notes in Computer Science: Applications of Evolutionary Computing, vol.5484, pp.808–817, 2009.
D’Ariano, A., Pranzo, M., “An advanced real-time train dispatching system for minimizing the propagation of delays in a dispatching area under severe disturbances”, Networks and Spatial Economics, vol.9, pp.63–84, 2009.
Corman, F., D’Ariano, A., Pacciarelli, D., Pranzo, M., “A tabu search algorithm for rerouting trains during rail operations”, Transportation Research Part B, vol.44, No.1, pp.175–192, 2010.
Schuitema, G., Steg, L., Rothengatter, J.A., “The acceptability, personal outcome expectations, and expected effects of transport pricing policies”, Journal of Environmental Psychology, vol.30, No.4, pp.587–593, 2010.
Jia, J., Hu, Q., “Dynamic ordering and pricing for a perishable goods supply chain”, Computers & Industrial Engineering, vol.60, No.2, pp.302– 309, 2011.