ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
R Prasanth1, L Anbarasu2, V Venmathi3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Multiplier plays an important role in digital signal processing systems but it consumes much power and area, In order to reduce the power and area occupied by the multiplier. We opt for fixed width multiplier. Our proposed method is to design fixed-width multiplier using Baugh-Wooley (BW) algorithm. It simplifies a structure of multiplier with the aim of reducing power and increasing performance of system. In this method two topologies are in particularly selected as the most effective ones. The first one is based on a uniform coefficient quantization, while the second topology uses a non uniform quantization scheme. The novel fixed-width multiplier using Baugh-Wooley algorithm exhibit better accuracy with respect to previous solutions the novel fixed-width multiplier topologies exhibit better accuracy with respect to previous solutions, close to the theoretical lower bound. The electrical performances of the proposed fixed-width multi-pliers are compared with previous architectures. It is found that in most of the investigated cases the new topologies are Pareto-optimal regarding the area-accuracy trade-off.
INTRODUCTION |
| In this project we are going to design the fixed-width multiplier using Baugh-Wooley (BW) algorithm. Fixed-width multiplier has the same bit width of input and output. In digital signal processing systems multiplier plays an important role but also it consumes more power and area. In order to reduce the power and area occupied by the multiplier unit fixed-width multipliers are designed. The fixed-width property simplifies the multiplier structure with the aim of improving power and speed. |
| In fixed width multiplication the product is fixed width to n-bits, the least-significant columns of the product matrix contribute little to the final result. To take advantage of this, fixed width multipliers do not form all of the leastsignificant columns in the partial-product matrix. Output is the weighted sum of partial-products. By eliminating more columns the area and power consumption of the arithmetic unit are significantly reduced & in many cases the delay also decreases. Area saving of a fixed width multiplier can be achieved by directly truncating n least significant columns and preserving n most significant columns This algorithm is a relatively straightforward way of doing signed multiplications. It uses only an array of full adders and a final Ripple Carry Adder (RCA). The main objective of this project is to design the fixed width BW multiplier using full-width BW multiplier which computes the 2n output as a weighted sum of partial-products. Many applications require an n bits output. A typical example is a digital, computationally intensive, ASIC in which the bit-width at the output of the arithmetic blocks is chosen on the basis of system related accuracy issues. Having a multiplier with an n bits output can also be useful in digital signal processors where the inputs and the outputs of the data path can be stored in registers with the same bit-width. A fixed-width multiplier is an n × n multiplier that computes, with a certain 7yapproximation, the most-significant bits of the product. |
| BW algorithm is an efficient way to handle the sign bit. BW multiplier uses only full adders. The main aim of this project is to reduce the area and power consumed by the fixed-width signed multiplier which uses both half adders and full adders for implementation. |
EXISTING FIXED WIDTH MULTIPLIER |
| Parallel multipliers are fundamental building blocks in multimedia and digital many applications, the inputs and the output of the multiplier have the same bit width. These circuits are denoted in literature as fixed-width multipliers or fixed width multipliers. The most obvious way to design a fixed-width multiplier uses a full-width multiplier, whose output is fixed width/rounded to n bits by n discharging the less-significant bits of the products. The fixed-width property, however, can be exploited to simplify the multiplier structure, with the aim of improving power and speed. Basically, one can discard some of the partial- products in the partial-products array to reduce the circuit complexity, at a price in terms of accuracy. This is the approach pursued in all the fixed-width multiplier architectures proposed in literature. |
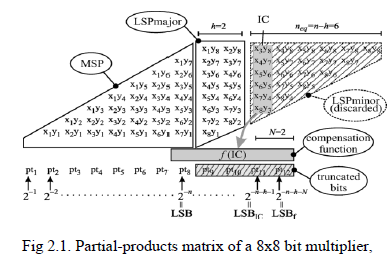 |
| fixed width with h=2 and using a variable-correction scheme to compute the result. Many error compensation methods have been proposed in literature. In the simplest approaches the compensation function is a fixed bias. Better accuracy is obtained in the so-called variable-correction (or adaptive) fixed-width multipliers. In these architectures the partial-products in the leftmost column of LSP minor are employed to obtain a probabilistic estimate of the sum of the elements of the LSP minor. In Fig 2.1 the partial-products in the leftmost column of LSP minor are highlighted in gray and are named Input Correction (IC), while f(IC) is the compensation function. |
| The choice f(IC) of is the critical step in the design of a fixed-width multiplier. This function should be efficiently implemented in hardware, and should provide, at the same time, a good estimate of the sum of the elements of the LSP minor. |
MINIMUM MEAN SQUARE COMPENSATION FUNCTION |
| In the following we will consider unsigned multipliers and we will also assume that the inputs of fractional values in (0,1). |
 |
PROPOSED BAUGH-WOOLEY ALGORITHM |
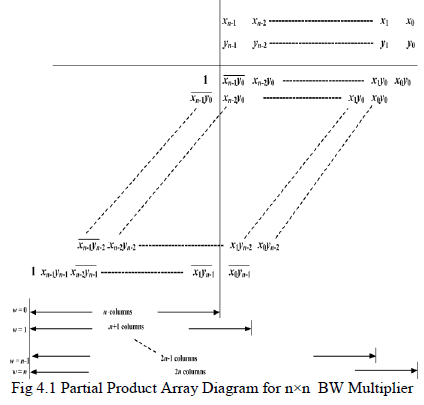
| The BW algorithm is a relatively straight forward way of doing signed multiplications. The fixed width multipliers derived from BW algorithm produce n-bit output product with n-bit multiplier and n-bit multiplicand. It is an efficient way to handle the sign bit. BW multiplier uses only full adders. All bit products are generated in parallel & collected through an array of full adder & final RCA. The creation of the reorganized partial-product array comprises three steps: |
| i) The Most Significant Bit (MSB) of the first N-1 partial-product rows and all bits of the last partial-product row, except its MSB, are inverted. |
| ii) A ‘1‘ is added to the Nth column. |
| iii) The MSB of the final result is negated. |
| Fig 4.1 shows the partial product array diagram for n×n BW multiplier. |
 |
| A. Truncation |
| Truncation is a method where the least significant columns in the partial product matrix are not formed. The amount of columns not formed in this way, T, defines the degree of truncation and the T Least Significant Bits (LSB) of the product always results in âÃâ¬Ãâ0‘. The algorithm behind fixed width multiplication is the same as when dealing with non fixed width multiplication regardless of the truncation degree. |
| B. Rounding |
| Conventionally an n-bit multiplicand and an n-bit multiplier would render a 2n-bit product. Sometimes an n-bit output is desired to reduce the number of stored bits. This is done in two steps. |
RESULTS |
| A. Electrical Performances |
| As we have pointed-out previously, our fixed width multipliers are well suited for effective tree based implementations. This happens for most of the previously proposed fixed width multipliers, use array multiplier with a ripple architecture, that are very slow and power hungry. These architectures can also be implemented with a much more effective carry-save TDM(three dimensional algorithm) reduction method. However, it is worth highlighting that the terms added to the partial-products matrix related to the compensation function are still obtained with a ripple AND/OR network, which increases power dissipation and propagation delay. In order to have a fair comparison among every approach, we have implemented every multiplier by using a carry-save TDM reduction tree followed by a fast carry-propagate adder. |
| B Area versus Accuracy Trade-Off |
| In practical applications the accuracy is generally constrained by system-level consideration. The designer goal is hence to achieve the lowest complexity for a specified accuracy. As we have highlighted in the previous sections, is a trade-off parameter between accuracy and complexity that can be used to obtain an optimal design. Therefore, a comparison of the different fixed width multipliers considering this trade-off between accuracy and complexity can be very useful.TDM are the one the efficient method to improve area than the previous proposed methods. As we have pointed out previously, our fixed-width multi-pliers are well suited for effective tree based implementations. |
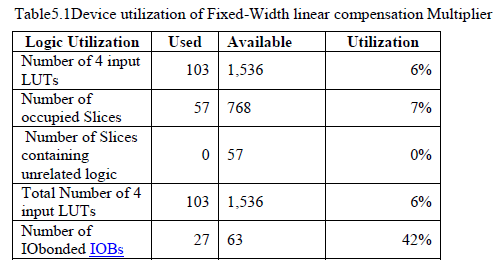
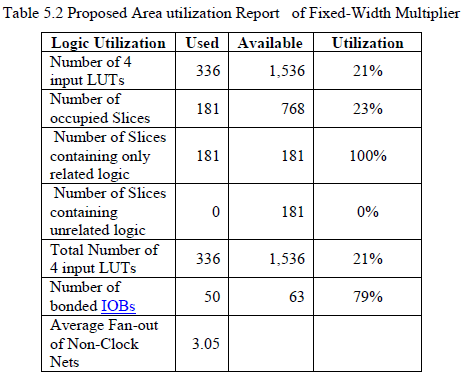
| This happens also for most of the previously proposed fixed-width multipliers. Therefore, in performing a comparison between various architectures, we implemented all the circuits by using a carry-save TDM reduction tree followed by a fast carry-propagate adder. As we have pointed out previously, our fixed-width multi-pliers are well suited for effective tree based implementations. This happens also for most of the previously proposed fixed-width multipliers. Therefore, in performing a comparison between various architectures, we implemented all the circuits by using a carry-save TDM reduction tree followed by a fast The area report of fixed-width Xilinx synthesis tool is shown in Table5.1. The total area is calculated based on the utilization of number of LUT‘s which is present in the device and the corresponding occupied slices. |
 |
 |
 |
| More area than fixed width. The simulation waveform of fixed-width linear multiplier using Xilinx simulation tool is shown in Fig 5.2. Given bits processed |
 |
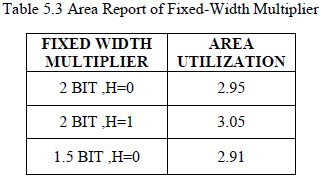 |
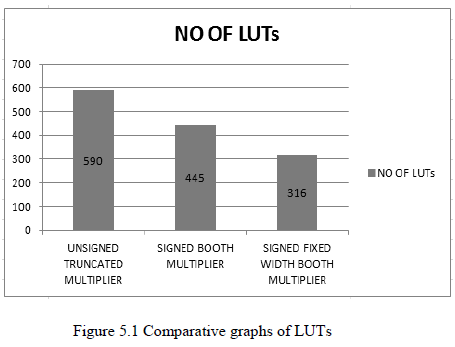
| Table 5.3 shows the Area report of fixed-width LINEAR COMPENSATION multiplier Xilinx synthesis tool. The total area is calculated based on the utilization of number of LUT‘s which is present in the device and the corresponding occupied slices. All the parameters are explained and specification is given above. It is clear normal multiplication requires more area than fixed width. The post synthesis implementation data of the 1.5 bits and 2bits fixed-width multipliers the approach using the auxiliary tree yields some advantage with respect to the standard architectures especially for 2 bits multipliers, where the number of duplicated partial-products is higher. For example, for and , the 2 bits fixed-width multiplier using the standard architecture results in increase area with respect to the multiplier of PRESENT Method. the fixed-width multipliers proposed in this paper are more accurate with respect to previously proposed architectures, the improvement being more evident for large. |
CONCLUSION |
| The truncated multiplier design by jointly considering the deletion, reduction, truncation and rounding of the partial product bits during tree reduction is analysed in terms of area and power using the Xilinx tool. The fixed width multiplier a subset of truncated multiplier designs, for a 10*10 unsigned multiplication the area and the power analysis is obtained. The truncated multiplier has a total error of no more than LUT and used in applications that require accurate results. The truncated multiplication is to be compared with extended booth multiplier to analyse the area and power using Xilinx tool. Modification is to done in the multiplier technique to obtain less power consumption. |
References |
|