ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
Balaji Naik.M1 , Ramana Reddy Gujjula2,Bojja Durga Bhavani3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
OFDM is known as one of the most favorable modulation techniques for communication over frequency selective wireless channels, and is widely used in telecommunication standards. But a major problem with OFDM is its high Peak to Average Power Ratio (PAPR), which decreases the efficiency of the power amplifier. New peak-toaverage power ratio (PAPR) reduction approach for MIMO-OFDM/A is developed based on the well known Complementary Code Modulation, is one of the techniques to reduce the PAPR of the OFDM signal.
Keywords |
||||||||||||||||||
| orthogonal frequency division multiplexing (OFDM), multiple input multiple output (MIMO), Peak to Average Power Ratio (PAPR), Complementary Coded modulation (CCK). | ||||||||||||||||||
INTRODUCTION |
||||||||||||||||||
| Multicarrier modulation, in particular its implementation as orthogonal frequency-division multiplexing (OFDM), is very popular for transmission over frequency-selective channels [6]. Since for future applications the use of antenna arrays is envisaged, parallel OFDM transmission, often denoted as MIMO- OFDM (multiple-input/multiple-output), is the most important candidate for next-generation wireless communication. In MIMO-OFDM system, the output is the superposition of multiple sub-carriers [2]. In this case, some instantaneous power outputs might increase greatly and become far higher than the mean power of the system when the phases of these carriers are same. This is also defined as large Peak-to-Average Power Ratio (PAPR). High PAPR is one of the most serious problems in MIMO-OFDM system. To transmit signals with high PAPR, it requires power amplifiers with very high power scope. These kinds of amplifiers are very expensive and have low efficiency-cost. If the peak power is too high, it could be out of the scope of the linear power amplifier. This gives rise to non-linear distortion which changes the superposition of the signal spectrum resulting in performance degradation. Because of non linear distortion in-band and out band interference occurs. If there are no measures to reduce the high PAPR, MIMO-OFDM system could face serious restriction for practical applications. To reduce PAPR several techniques are proposed without worrying about performance at the BER. Several techniques have been proposed to mitigate the high PAPR of OFDM signals [3]. tone reservation (TR) [9], tone injection (TI) [9], and active constellation extension (ACE) [5] change constellation points for some subcarriers to reduce the PAPR. the use of Golay complementary sequences [3] to reduce PAPR within 3 dB was proposed in this paper. | ||||||||||||||||||
PAPR AND EFFECTS IN OFDM |
||||||||||||||||||
| As explained earlier, one of the major drawbacks of OFDM is the very high peak-to-average power ratio (PAPR).Multiple sub carrier are increased exponentially, PAPR of OFDM system increases results the power amplifier past its saturation level[1]. The mathematical model for transmitted OFDM signal can be represented as | ||||||||||||||||||
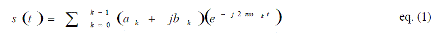 (1) (1) |
||||||||||||||||||
| Where k is the number of sub-carriers, ak and bk is the real and imaginary components of the complex modulating symbols of the k sub-carriers respectively. If the number of subcarriers are large, the central limit theorem says that the probability distribution function of the sum of a large number of random variables approaches (both in-phase and quadrature phase) a Gaussian distribution with zero mean and mean squared (variance) value 1/2. Since both in-phase and quadrature components are Gaussian, the absolute amplitude is Rayleigh-distributed. Thus, high PAPR is a consequence of the constructive superposition of high sub-carrier values of numerous sub-carriers [4]. The PAPR parameter in any OFDM symbols can be calculated by using the following equation: | ||||||||||||||||||
 (2) (2) |
||||||||||||||||||
| Where E [.] denotes expected value. | ||||||||||||||||||
Effects of High PAPR: |
||||||||||||||||||
| In Large PAPR caused at the power amplifier at the transmitter end causes the amplifier to switch from linear region of operation to non-linear region, the compression region near saturation. These non-linearities cause spectral spreading, intermediation and distortion of signal constellation. In other words, it would cause both in band and out of band interference to the signals. As the in band interference increases, the Bit Error Rate (BER) increases primarily due to injected broad band noise caused by clipping and in case through distorting of the signal constellation. The out band interference causes interference to adjacent channels. Therefore, it is essential for power amplifiers to operate in the linear region. | ||||||||||||||||||
POLYPHASE COMPLEMENTARY CODES |
||||||||||||||||||
| Presence of large number of independently modulated sub-carriers in an OFDM system the peak value of the system can be very high as compared to the average of the whole system. This ratio of the peak to average power value is termed as Peak-to-Average Power Ratio this is main disadvantage of OFDM, to reduce PAPR here we are using Golay Complementary Codes. Complementary codes or sequences are sets of binary spreading codes characterized by the property that the sum of their auto correlation sequences exhibit no side lobes hence correspond to a single impulse at zero offset. There are some basic coding rules by which a single pair of Complementary Codes can be the basis for the construction of 2^6 pairs of complementary codes by performing or not performing the following six operations [6]: | ||||||||||||||||||
| 1. Interchanging both series | ||||||||||||||||||
| 2. Reversing and conjugating both series | ||||||||||||||||||
| 3. Altering second series | ||||||||||||||||||
| 4. Altering first series. | ||||||||||||||||||
| 5. Altering elements of even order in both series. | ||||||||||||||||||
| 6. Reversing and conjugating first series | ||||||||||||||||||
| Polyphase Complementary Code is a sequence having complementary properties, the elements of which have phase parameters. For example, the polyphase sequence used in Complementary Code modulation uses four different phase angles. One of the most interesting properties of Complementary Codes is that they are a pair of binary sequences whose sum of autocorrelation of individual sequences yields zero except at zero shifts. The same property is also extended to polyphase complementary codes[3]. This property is used in OFDM to reduce the PAPR. The stages of the Complementary Codes generating filters are formed by delay elements and butterflies as shown in Fig.1 | ||||||||||||||||||
| The delay elements are nothing but all pass networks with unity gain at all frequencies, only contributing phase shift to the transfer function. So we can modify the Complementary Code generating filter by replacing the delay register segment with another all-pass register segment with an associated arbitrary phase rotator [6][8]. Thus binary complementary codes relationship can be re-written to include phase resulting in Polyphase Complementary Codes as shown in Fig.2 | ||||||||||||||||||
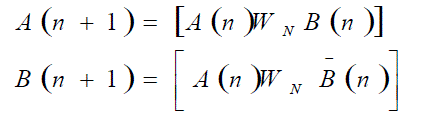 (3) (3) |
||||||||||||||||||
| For a pair of sequences, a and b, each of length N, to be complementary the following property must true | ||||||||||||||||||
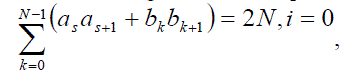 (4) (4) |
||||||||||||||||||
| otherwise = 0 , where i≠0 | ||||||||||||||||||
| The Fourier transform of an autocorrelation function of a sequence is its power spectral density. Hence, taking the Fourier transform of the above equation yields, |A(ω)|^2 + |B(ω)|^2 = 2N where |A(ω)|^2 and |B(ω)|^2 are the individual power spectral densities of a and b respectively. Thus the maximum value of the individual power spectrum is limited to 2N, (i.e.) |A(ω)|^2 ≤ 2N Therefore, assuming the power of sequence a is equal to unity, Average |A(ω)|^2 = N Hence, PAPR ≤ 2N/N ≤ 2 Thus it can be concluded that by using Polyphase Complementary Codes(PCC) the value of the PAPR can be restricted to the maximum value of 2. | ||||||||||||||||||
COMPLEMENTARY CODED OFDM |
||||||||||||||||||
| The PAPR of OFDM system is restricted to the maximum value of 2 using PCC. | ||||||||||||||||||
| The complementary codes are applied as the phases of set of complex sinusoids of an Inverse Fourier Transform (IDFT) of an OFDM modulator [4]. The time sequence formed at the output of IFFT block has a peak mean square value no greater than the average mean square value. Thus peak to average power of the signal is confined to a maximum value of 2. | ||||||||||||||||||
Generation Of Length-8 CC: |
||||||||||||||||||
| The modulation scheme used is Quadrature Phase Shift Keying (QPSK). So the four QPSK phases are encoded into original data. One way of doing the phase encoding is applying the first phase to all the alternating elements of the code, second phase to all the odd and even pairs, third phase to all the odd and even quads and the fourth phase is applied to the entire code as shown in the filter structure of Fig 4. | ||||||||||||||||||
| For a delta function as the input, the upper path before the first group of summation blocks has unity gain. The lower path has a unit delay and a phase rotator with phase. The output of the upper summation block is {1+exp(j)} and the output of lower summation block is {1- exp(j)}. The next all-pass filter bank has unity gain in the top path and two units of delay and a phase rotator with phase[7]. The output of the upper summation block is {1+exp(j)} and the output of lower summation block is {1- exp(j)}. The next all-pass filter bank has unity gain in the top path and two units of delay and a phase rotator with phase[5]. The output of the upper summation block is {1+exp(j)} and the output of lower summation block is {1- exp(j)}. Finally, a common phase is applied to the entire sequence. The output of the entire lower and upper summation block can be represented by equations as shown: | ||||||||||||||||||
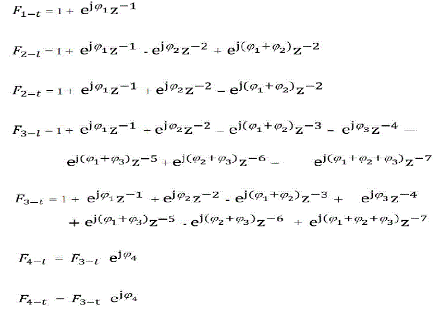 |
||||||||||||||||||
| The buildup of CCK OFDM symbol can be described by matrix equations. A generator matrix is used to map the phases of the QPSK symbols into the phases of the subcarriers. The relationship between the M-ary PSK data point phases and the subcarrier phases is given by the matrix equation: | ||||||||||||||||||
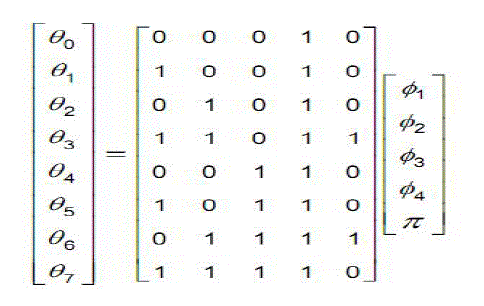 |
||||||||||||||||||
Generation Of Length-16 CC |
||||||||||||||||||
| For generating a Complementary Code of length-16, 5 QPSK phases are mapped into 16 subcarrier phases. The filter structure used for achieving this is shown in Fig 5. | ||||||||||||||||||
| The working of the filter structure is same as that of the filter structure of length-8 Complementary Code. The equations after each and every stage can be easily calculated from the relationship between 5 QPSK input phases and 16 subcarrier phases as shown in matrix below: | ||||||||||||||||||
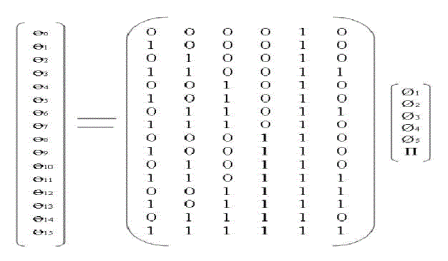 |
||||||||||||||||||
RESULTS AND DISCUSSION |
||||||||||||||||||
| Fig. 6, shows the time series of Standard OFDM and the Complementary Coded OFDM packet The peak and the average value of the Standard OFDM signal is 0.6284 and 0.2220.Thus, the PAPR value for Standard OFDM signal is nearly equal to 2.6. Similarly for the peak and average value of 0.25 and 0.1631 for the Coded OFDM signal, the PAPR value is nearly equal to √2. Thus, PAPR is reduced considerably. The coding rate for length-8 Complementary Code sequence is 4/8, since 4 phases of QPSK are mapped to 8 phases. | ||||||||||||||||||
| Fig.7. shows the probability of amplitude crossing for both standard and complementary coded OFDM signal. The figure shows that the probability of the amplitude of Coded OFDM signal to cross √2 is zero whereas for standard OFDM, there is significant probability that the amplitude would cross √2. | ||||||||||||||||||
| Fig.8 shows the time series of Complementary Coded OFDM packet and the probability of amplitude crossing for standard OFDM, length-2 and length-16 Complementary Coded OFDM sequence. The peak and the average value for length-16 Complementary Coded OFDM sequence is 0.17765 and 0.11815 respectively. So the PAPR is 1.4952. But the problem with length-16 CC OFDM sequence is the coding rate. The coding rate is 5/16 as it maps 5 input QPSK phases to 16 phases. Such high coding rate is not a good trade-off for low PAPR. | ||||||||||||||||||
CONCLUSION |
||||||||||||||||||
| In this paper, we analyzed the performance in terms of PAPR in OFDMA by using Complementary Code modulation. Here we used length-8 and length -16 Complementary Code (sub-carrier) are applied, results PAPR reduces less than 3dB. With increase in number of sub-carriers, the length of complementary code increases which also results in increased complexity. To avoid this problem, the number of sub-carriers are split in smaller groups and shorter length codes is applied to each code, This results in low PAPR i.e the value is nearly equal to √2. Thus, PAPR is reduced considerably. | ||||||||||||||||||
Figures at a glance |
||||||||||||||||||
|
||||||||||||||||||
References |
||||||||||||||||||
|