International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Menu

ISSN ONLINE(2319-8753)PRINT(2347-6710)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Reed-Solomon Coded OFDM with Unique Word as Guard Interval

Nitinkumar M.Pachkawade1, Manoj M.Dongre2
  1. M.E.Student, Department of EXTC, RAIT, Nerul, Navi-Mumbai, Maharastra India
  2. HOD, Department of EXTC, RAIT, Nerul, Navi-Mumbai, Maharastra, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper gives an idea for a new transmit signal structure for OFDM(Orthogonal Frequency Division Multiplexing).To avoid the interference between to signal we always require a guard band interval using cyclic prefix. But instead of that here a new term is used which is nothing but Unique Word Length where deterministic signal is used. Since Unique Words represent known sequences, they can advantageously be used for synchronization and channel estimation purpose. Furthermore it also generates the complex reed-Solomon (RS) code structure within the structure of sub-carriers which act as a unique word length code. To further improve the bit error ratio behavior of the system, winner smoother was used to succeeding a zero forcing stage at the receiver. These beneficial properties are achieved while additionally featuring around the same bandwidth efficiency as conventional CP-OFDM.In this paper with the help of simulation we highlight the advantages spectral properties and the bit error ratio performance(BER) performance of nonsystematic coded UW-OFDM and CP-OFDM in additive white Gaussian Noise (AWGN) as well as frequency selective environment

Keywords
Cyclic Prefix (CP), channel coding/decoding, Equalization, interleaving/deinterleaving Reed-Solomon codedOFDM,Synchoronisation,Unique word generator

I. INTRODUCTION
In the Conventional OFDM signaling systems subsequent symbols are separated by guard intervals which are usually implemented as cyclic prefix (CPs)[1].CPs is used as a guard interval in order to reduced ISI and for cyclicity. In this paper we propose to use known sequence which we call unique word (UW’s) instead of cyclic prefix .The technique of UWs has already been investigated in -depth for SC/FDE system[2],where the introduction of unique word in time domain is straightforward since the data symbol are also defined in time domain .In this paper we will show how the unique word can also be introduced in OFDM time domain symbol even though the data QAM (Quadrature Amplitude Modulation )symbols are defined in frequency domain .Fig 1 Compares the Transmit data structure of CP and UW based transmission in time domain[3].Both structures make sure that the linear convolutation of an OFDM symbols with impulse response of dispersive (eg multipath) channel appears as a cyclic convolutation at the receiver side . Nevertheless there are also some fundamental differences CP & UW based transmission The CP is a random sequence whereas the UW is deterministic. Hence, the UW can be optimally designed for particular needs like synchronization and/or channel estimation purposes at the receiver side .In UW-OFDM the guard interval is part of the DFT interval, whereas this is not the case for CP-OFDM which improve the bit error ratio (BER) performance. UW-OFDM has the superior spectral density of the generated waveform than CP-OFDM. If a unique word (UW) is chosen in advance and introduced at the end of each OFDM symbol, cyclicity appears, too. The better way of guard interval is done by using unique word (UW) .This solves the disadvantages of CP having medium BER behavior and bandwidth efficiency. Since unique words represent known sequences, they can advantageously be used for synchronization and channel estimation purposes. Furthermore, the proposed approach introduces a complex number Reed-Solomon (R-S) code structure within the sequence of subcarriers.Viterbhi algorithm is used for coding & decoding.

II. RELATED WORK
OFDM is used in wide verity of applications such as: several high frequency military systems, high speed modem, digital mobile communication, high density recording, ADSL, VDSL, DAB, DVB and HDTV. Different methods are used for insertion of guard interval in OFDM. In conventional OFDM signaling, subsequent symbols are separated by guard intervals, which are usually implemented as cyclic prefixes (CPs)[1]. In order for the cyclic prefix to be effective (i.e. to serve its aforementioned objectives), the length of the cyclic prefix must be at least equal to the length of the multipath channel. Although the concept of cyclic prefix has been traditionally associated with OFDM systems, the cyclic prefix is now also used in single carrier systems to improve the robustness to multipath..The CP is less useful for purposes like channel estimation, equalization as long as the content of the CP is not known and varied with every single block. . In this paper we proposed to use known sequence which we called Unique word (UW’s) instead of cyclic prefix. This technique has already been used in –depth for SC –FDE systems [2]. Since Unique word is represents known sequence, they can advantageously be used for synchronization and channel estimation Purpose Another difference between CP and UW is that UW is a part of DFT (Discrete Fourier Transform ) interval ,whereas CP is not due to this fact the UW OFDM has bandwidth efficiency as in Conventional CP-OFDM. Due to this the length of one OFDM symbol reduces from �������� +����` to �������� . The CP is random sequence whereas UW is deterministic therefore the UW can advantageously be utilized for synchronisization an channel estimation Purposes. Figure 4 compares CP-OFDM and UW –OFDM.
Both statements hold for OFDM-as well as for SC/FDE-systems. However, in OFDM different to SC/FDE the introduction of UWs in time domain leads to another fundamental and beneficial signal property: A UW in time domain generates a word of a complex number RS (Reed Solomon)-code along the sub carrier symbols. Another interpretation of this fact which we prefer here is an introduction of correlations along the sub carriers. These correlations can advantageously be used as a-priory knowledge at the receiver to significantly improve the BER (bit error ratio) performance by applying a simple LMMSE Wiener smoother succeeding the common zero forcing (ZF) Equalizer. The another scheme is KSP (Known Symbol Padded) the receiver side. The broadly known KSP-OFDM uses a structure similar to UW-OFDM ,since the known symbol(KS) is a deterministic sequence .The most important difference between KSP – OFDM & UW-OFDM) is the fact that UW is a part of DFT interval, whereas KS is not. The generation of UW within the DFT interval introduces the correlation among the subcarrier which was advantageneously exploited by receiver to improve the bit error rate performance Whilest in both the scheme the deterministic sequences can be used for synchronization and channel estimation purposes ,these correlations are not present in KSP-OFDM..

III. PROJECT METHODOLOGY
In this project we will design OFDM transmitter and receiver with UW concept using reed Solomon coder and decoder. The block diagram of the system is as given below. The input is random number with 64 0r 128 bits and output is BERgraphs.
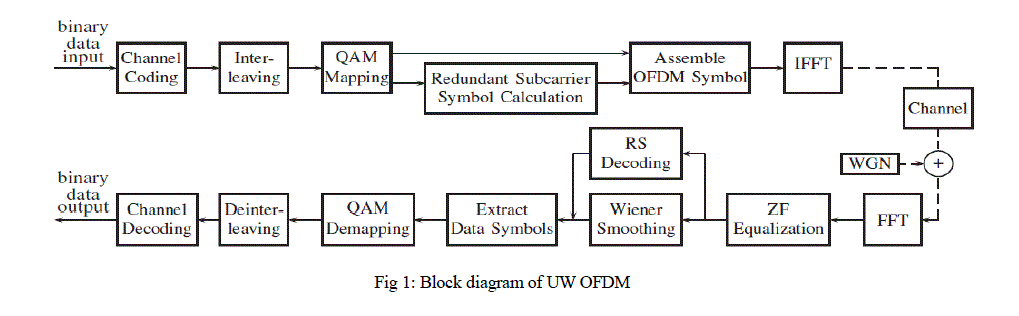image
Input is binary data which is given to channel coding block for encoding channels. It will send to QAM modulator for modulating or mapping signal through interleaving block. Reed Solomon encoding is done on QAM output signal. Unique word Symbols are inserted, IFFT is apply on than signal, which is pass trough channel where white Gaussian noise is added, we apply FFT on that and remove UW symbols, after this exactly opposite process takes place as transmitter side.
Steps for Methodology:
1. Channel coding/decoding: To avoid this domination by the weakest subcarriers, forward error correction coding is essential. By using coding across the subcarriers, error of weak subcarriers can be corrected up to a certain limit that depends on the code and the channel. A powerful coding means that the performance of an OFDM link is determined by the average received power, rather than by the power of weakest subcarrier. At the receiver the encoded data is recovered by decoding which is exact reverse of encoding.
2. Interleaving/Deinterleaving: The interleaving is applied to randomize the occurrence of bit errors prior to decoding. At the transmitter, the coded bits are permuted in a certain way, which makes sure that adjacent bits are separated by several bits after interleaving. At the receiver the reverse permutation is performed before decoding. A commonly used interleaving scheme is block interleaver, where input bits are written in a matrix column by column and read out row by row. Instead of block interleaver, it is also possible to use a convolution interleaver.
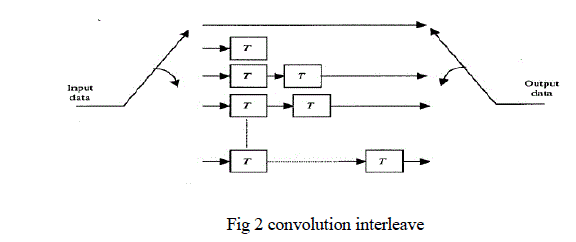image
This interleaver cyclically writes each input symbol or bit into one of k shift registers that introduces a delay of 0 to k- 1 symbol duration. The shift registers are read out cyclically to produce the interleaved symbols
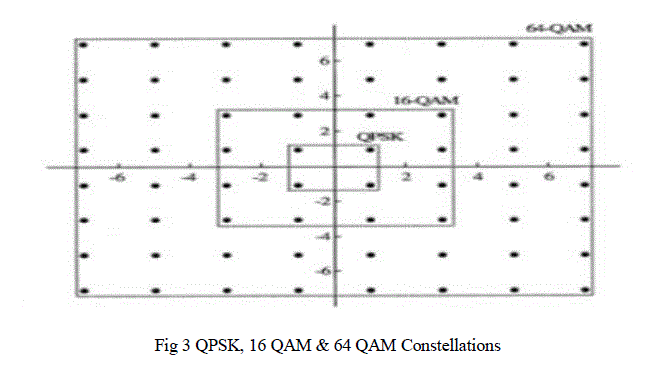
3. QAM mapping/Demapping: Quadrature amplitude modulation (QAM) is the most popular type of modulation in combination with OFDM. Especially rectangular constellation are easy to implement as they can be split in to independent pulse amplitude modulated (PAM) components for both the in-phase and the quadrature part. Noise immunity is better in case of QAM because signal vectors differ not only in phase but also in amplitude Fig.4 is constellations of QPSK,16 QAM .In the receiver, the incoming QAM symbols have to be demapped..
4. FFT/IFFT: IFFT modulates a block of input QAM values on to a number of subcarriers. In the receiver, the subcarriers are demodulated by an FFT, which performs the reverse operation of an IFFT. In fact, the IFFT can be made using an FFT by conjugating input and output of the FFT and dividing the output by the FFT size. This makes it possible to use the same hardware for both the transmitter and the receiver. Of course, this saving in complexity is only possible when the modem does not have to transmit and receive simultaneously, which is the case for the standard. In practice, this transform can be implemented very efficiently by the IFFT because, IFFT drastically reduces the amount of calculations by exploiting the regularity of the operation in the IDFT.
image
5. Equalization: When the signal is passed through the channel, distortion is introduced in the terms of amplitude and delay creating problem of ISI. This distortion can be compensated with the help of equalizers. Zero Forcing Equalizer refers to a form of linear equalization algorithm used in communication systems which inverts the frequency response of the channel. The Zero-Forcing Equalizer applies the inverse of the channel to the received signal, to restore the signal before the channel. It has many useful applications. The name Zero Forcing corresponds to bringing down the intersymbol interference (ISI) to zero in a noise free case. This will be useful when ISI is significant compared to Noise.
6. R-S Decoding/Wiener Smoothing: Either the Wiener smoother or algebraic RS decoder is applied to the OFDM symbol, depending on the specific receiver concept. A class of nonbinary codes that does reach the above bound are the reed- Solomon codes. These codes have great power and utility, and are today found in many applications from compact disc players to deep-space applications. Reed-Solomon codes are nonbinary cyclic codes with symbols made up of m-bit sequences, where m is any positive integer having a value greater than 2.R-S (n, k) codes on m-bit symbols exist for all n and k for which 0 < k < n < 2m + 2 where k is the number of data symbols being encoded, and n is the total number of code symbols in the encoded block. For the most conventional R-S (n, k) code,(n, k) = (2m - 1, 2m - 1 - 2t) where t is the symbol-error correcting capability of the code, and n – k = 2t is the number of parity symbols. An extended R-S code can be made up with n = 2m or n = 2m + 1, but not any further.
The introduction of UWs in time domain leads to another fundamental and beneficial signal property: A UW in time domain generates a word of a complex number RS (Reed Solomon)-code in the OFDM frequency domain symbol vector. Therefore, the UW could be exploited for algebraic error correction or (more appropriately) for erasure correction for highly attenuated subcarriers. However, as it turns out, algebraic RS decoding leads to solving a very illconditioned system of equations and thus cannot achieve a reasonable solution, as soon as even only little noise is present in the system. Another interpretation of the introduction of UWs in time domain is that it leads to correlations along the subcarriers. Therefore, a receiver based on a Bayesian estimation is obvious, too. A receiver based on a Bayesian estimation will in fact significantly improve the BER behavior by exploiting the covariance matrix of the subcarrier symbols.
7. Unique Word Generation: In conventional OFDM signaling, subsequent symbols are separated by guard intervals, which are usually implemented as cyclic prefixes. In UW-OFDM it is proposed to use known sequences, which we call unique words, instead of cyclic prefixes. The technique of using UWs has already been investigated in-depth for SC/FDE systems, where the introduction of unique words in time domain is straightforward, since the data symbols are also defined in time domain. Unique words can also be introduced in OFDM time domain symbols, even though the data QAM (quadrature amplitude modulation) symbols are defined in frequency domain. Furthermore, many optimized receiver concepts adjusted to the novel transmit signal structure are possible.
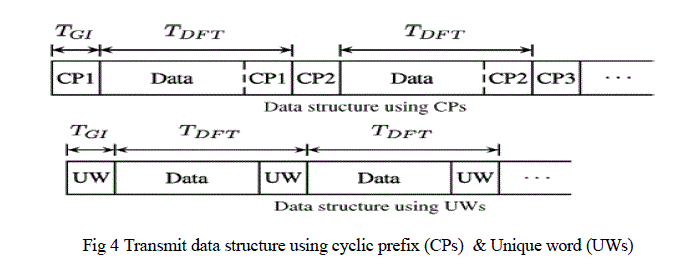image
The figure 4 compares the transmit data structure of CP and UW based transmission in time domain. Both structures make sure that the linear convolution of an OFDM symbol with the impulse response of a dispersive (e.g. multipath) channel appears as a cyclic convolution at the receiver side. Nevertheless, there are also some fundamental differences between CP and UW based transmission: The UW is part of the DFT (discrete Fourier transform) interval, whereas the CP is not. Although we need to spend dedicated subcarriers - which we call redundant subcarriers - for creating a UW in the time domain, we achieve approximately the same bandwidth efficiency in our approach as in conventional CPOFDM. This is due to the fact that the length of one OFDM symbol reduces from T_DFT + T_GI to T_DFT.The CP is random, whereas the UW is a known deterministic sequence. Therefore, the UW can advantageously be utilized for synchronization and channel estimation purposes. Both statements hold for OFDM as well as for SC/FDE systems. However, in OFDM - different to SC/FDE - the introduction of UWs in time domain leads to another fundamental and beneficial signal property: A UW in time domain generates a word of a complex number RS (Reed Solomon) code along the subcarrier symbols. Another interpretation of this fact which we prefer here, is an introduction of correlations along the subcarriers. These correlations can advantageously be used as a-priori knowledge at the receiver to significantly improves the BER (bit error ratio) performance.

IV. SIMULATION & RESULTS
In this work we introduces a novel OFDM signaling concept where the guard interval are built by unique words instead of cyclic prefix .This Proposed approach introduces a complex number of Reed-Solomon code structure within the sequence of subcarrier As an important conclusion we can state that besides the possibility to use the UW for synchronization and channel estimation purposes.
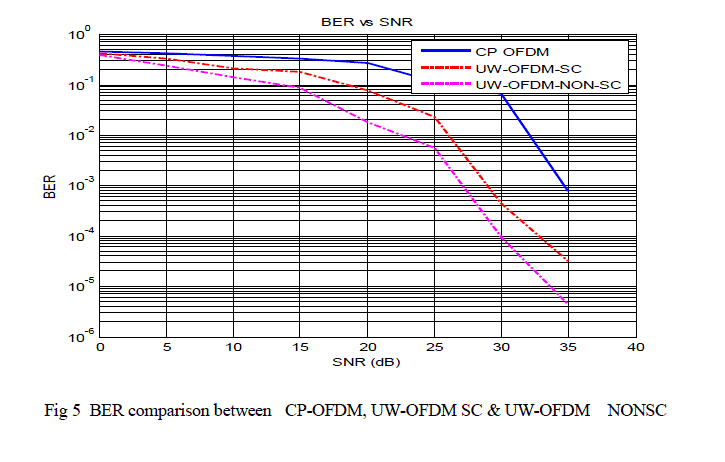image
Fig. 5 shows the comparison between CP OFDM and UW approach for systematic & nonsystematic systems. Systematic coded UW-OFDM performs slightly worse compared to CP-OFDM .But Non Systemic coded UW-OFDM outperforms CP OFDM & Systemic coded OFDM (with LMMSE data estimator) respectively. We consider this as a remarkable performance of Non Systemic coded UW-OFDM
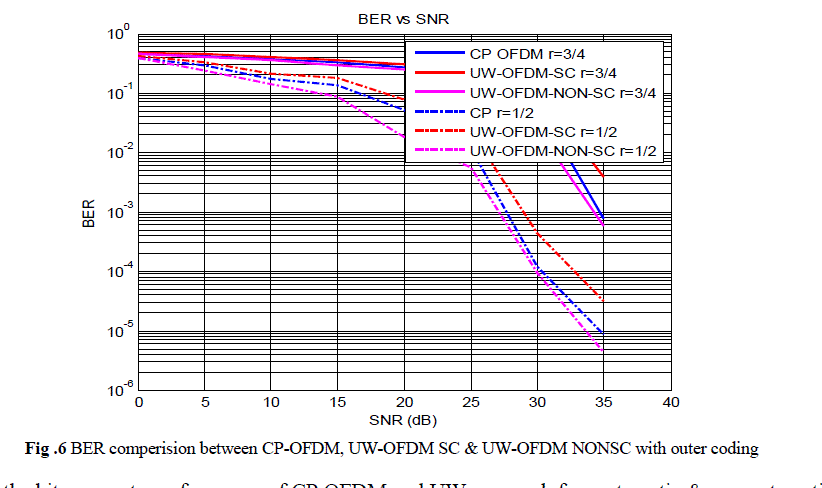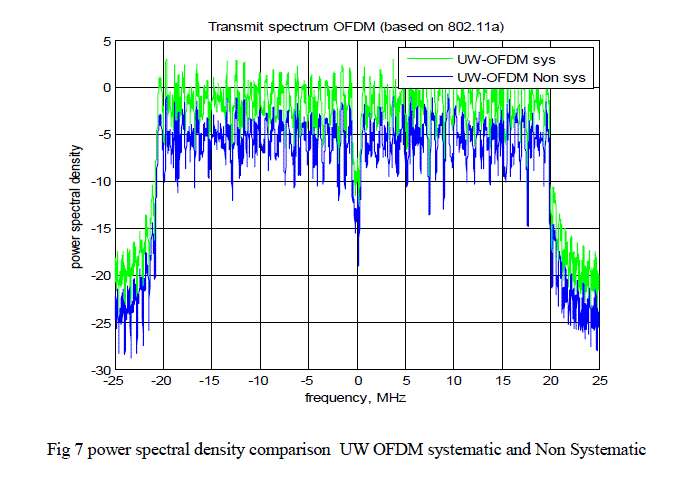
image
fig 6.compares the bit error rate performance of CP OFDM and UW approach for systematic & nonsystematic systems. with outer coding with r = ½ and r=3/4.For both outer coding rates UW-OFDM outperforms the CP-OFDM.and non systematic coded UW-OFDM shows by far the best performance.Fig.7 shows power spectral density comparison UW OFDM systematic and Non Systematic, from the figure it is clear that non systematic coded UW-OFDM has better spectral properties than Systematic coded UW-OFDM.
image

V. CONCLUSION
In this work we introduce the concept of UW-OFDM where unique word is used as a guard interval instead of cyclic prefix. The proposed approach introduces a complex number Reed –Solomon code structure within the sequence of subcarrier. An important conclusion we can state here that unique word give better channel estimation and Synchronization. We also conclude that Non systematic coded UW-OFDM has advantageous spectral properties and superior bit error rate performance than CP-OFDM and systematic coded UW-OFDM..

References
  1. R. van Nee, R. Prasad, OFDM for Wireless Multimedia Communications, Artech House Publishers, Boston, 2000.
  2. H. Witschnig, T. Mayer, A. Springer, A. Koppler, L. Maurer, M. Huemer, R. Weigel, ‖A Different Look on Cyclic Prefix for SC/FDE‖ In the Proceedings of the 13th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC 2002), Lisbon, Portugal, pp. 824-828, September 2002.
  3. M. Huemer, C. Hofbauer, J.B. Huber, ―The Potential of Unique Words in OFDM‖, In the Proceedings of the 15th International OFDMworkshop (InOWo’ 10), Hamburg, Germany, pp. 140 -144, September 2010.
  4. A. Onic and M. Huemer, ―Direct versus two-step approach for unique word generation in UW-OFDM,‖ in Proc. 15th Int. OFDM Workshop, Hamburg, Germany, Sep. 2010, pp. 145–149.
  5. Mario Huemer, Christian Hofbauer and Johannes B.huber ―Non-Systematic Complex Number RS coded OFDM by Unique word Prefix ― IEEE transction on Signal processing volume 60 January 2012.
  6. C. Hofbauer, M. Huemer, and J. B. Huber, ―Coded OFDM by unique word prefix,‖ in Proc. IEEE Int. Conf. Commun. Syst. (IEEE ICCS), Singapore, Nov. 2010, 5 pp.
  7. M. Huemer, A. Onic, and C. Hofbauer, ―Classical and Bayesian linear data estimators for unique word OFDM,‖ IEEE Trans. Signal Process., vol. 59, no. 12, pp. 6073–6085, Dec. 2011.
  8. A. Czylwik, ―Comparison between adaptive OFDM and single carrier modulation with frequency domain equalization,‖ in Proc. IEEE Veh. Technol. Conf. (VTC), Phoenix, AZ, May 1997, pp. 865–869.
  9. L. Deneire, B. Gyselinckx, and M. Engels, ―Training sequence versus Cyclic prefix: A new look on single carrier communication,‖ in Proc. IEEE Int. Conf. Global Commun. (IEEE GLOBECOM), Nov. 2000, pp. 1056–1060.
  10. R. Cendrillon and M. Moonen, ―Efficient equalizers for single and multi-carrier environments with known symbol padding,‖ in Proc. IEEE Int. Symp Signal Process Its Appl. (ISSPA), Aug. 2001, pp. 607–610
  11. M. Huemer, C. Hofbauer, and J. B. Huber, ―Unique word prefix in SC/FDE and OFDM: A comparison,‖ in Proc. IEEE GLOBECOM Workshop Broadband Single Carrier Freq. Domain Commun. (BSCFDC), Miami, FL, Dec. 2010, pp. 1321–1326.
  12. M. Muck, M. de Courville, and P. Duhamel, ―A pseudorandom postfix OFDM modulator—Semi-blind channel estimation and equalization,‖ IEEE Trans. Signal Process., vol. 54, no. 3, pp. 1005–1017, Mar. 2006.
  13. L. Jingyi, P. Joo, and J. Ro, The Effect of Filling UniqueWords to Guard Interval for OFDM, Document IEEE C802.16a-02/87, IEEE 802.16 Broadband Wireless Access Working Group, Sep. 2002.
  14. M. Huemer, C. Hofbauer, and J. B. Huber, ―Complex number RS Coded OFDM with systematic noise in the guard interval,‖ in Proc. 44th ASILOMAR Conf. Signals, Syst., Comput., Pacific Grove, CA, Nov. 2010, pp. 1023–1027.