International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

REFINEMENT OF POWER SYSTEM STABILIZER

Dhivya Grace Varghese1 and Hassena K A2
  1. PG Scholar [Power System], Saintgits College Of Engineering, Kottayam, India
  2. Assistant Professor, Saintgits College Of Engineering, Kottayam, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

fractional-order power system stabilizer (FoPSS) is introduced to control the frequency and the terminal voltage deviation in a power system connected to an infinite bus. FoPSS yields satisfactory results when there is drastic load change in long transmission lines. MATLAB/Simulink simulation is used to show the improvement of system’s performance when FoPSS is used. FoPSS is more superior to the classical integer-order power system stabilizers (IoPSS)

Keywords
FoPSS Fractional order Power System Stabilizer
IoPSS Integer order Power System Stabilizer
PSS Power System Stabilizer
q-axis Quadrature Axis
d-axis Direct Axis
FOC Fractional Order Controller
AVR Automatic Voltage Regulator

INTRODUCTION
The PSS compensates the local and inter-area mode of frequency oscillations that appears in power systems connected to long transmission lines. These oscillations could go up to ±1 Hz off the nominal value. The stability analysis of power systems using adaptive or sliding mode techniques is not straightforward especially when it comes to online tuning. For instance, different techniques of sequential design of PSS’s were adopted to damp out inter area mode of oscillations one at a time. However, this approach may not lead finally to an overall optimal choice of PSS parameters; the stabilizers designed to damp one mode can produce adverse effects in other modes.
A classical integer-order lead PSS with a washout component is usually used to stabilize power systems. Since most of these controllers have at least five parameters to tune, and exhibit narrow band phase compensation around a desired operating point, there is a need to implement more robust PSS with fewer number of parameters to adjust. Fractional-order controllers exhibit a flat phase response that depends on the fractional-order dynamics. The flat phase characteristics yield a robust FoPSS, which makes it capable of accommodating wider range of disturbances than the IoPSS.

FRACTIONAL-ORDER POWER SYSTEM STABILIZERS
A FoPSS was successfully implemented to control a single machine connected to an infinite-bus system [1]. The FoPSS enjoys a memory effect, which exhibits a satisfactory performance in most practical applications. In spite of the design complexity of the FoPSS, this feature gives the fractional-order compensators a leading edge over their integerorder counterparts. A typical FoPSS may be described by the following transfer function:
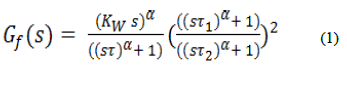image
image

MODEL 2.1
To reduce the modelling complexity, while still retaining key generator dynamics effects. The sub-transient effects that produce a demagnetizing effect due to a change in the rotor by the damping winding are neglected in this model. However, the transient effects of the damping windings are still taken into account. The following simplifying assumptions are made in Model 1.1.
image
1) Block Diagram Modeling of Synchronous Generator
The stator resistance is assumed to be negligible.
The following equations in the s-domain characterize Model 2.1.
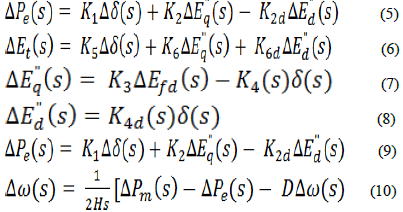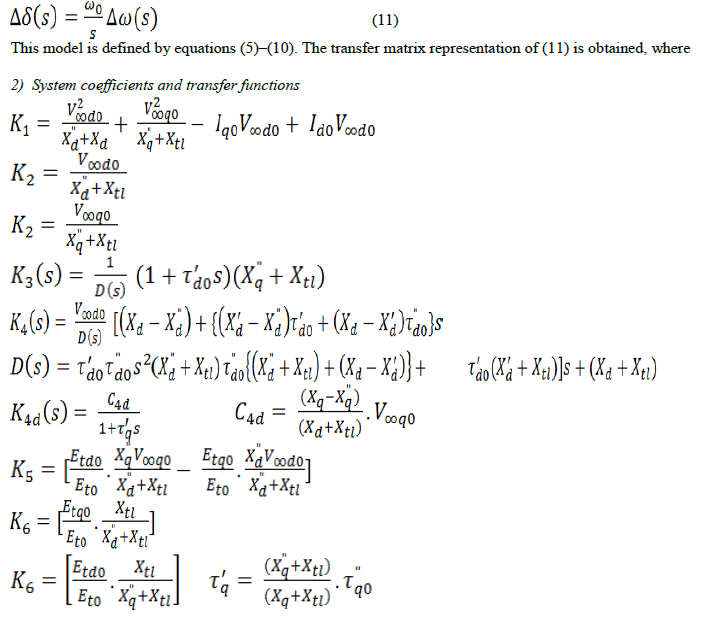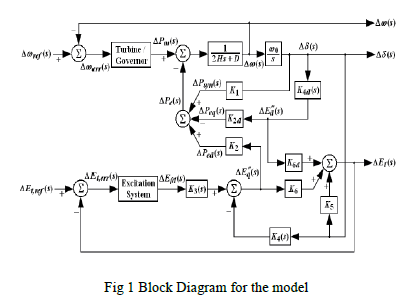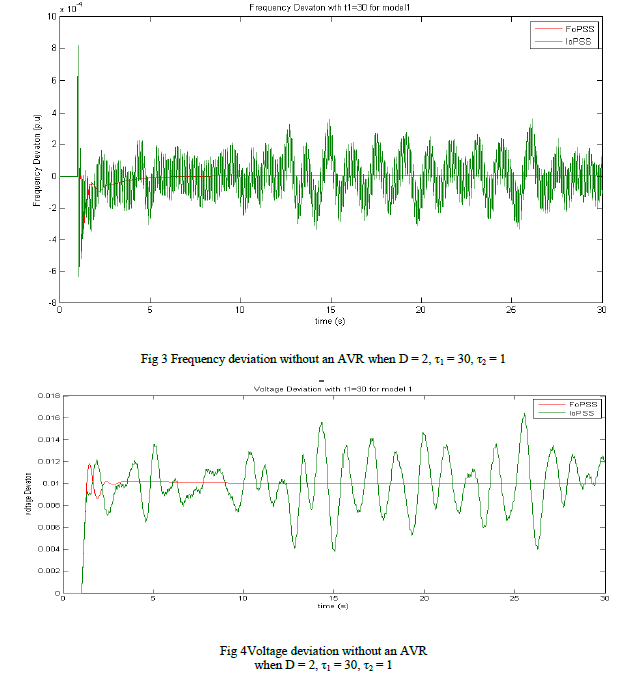
image
image
image
3) Stabilization with an AVR
Excitation system is a key element in the dynamic performance of any electrical power generator. Since accurate excitation is of great importance in bringing the machine into synchronization, and since an AVR malfunction could destabilize the overall system. It is needed to investigate the effect of both stabilizers onto the system with and without an AVR.

NUMERICAL RESULTS
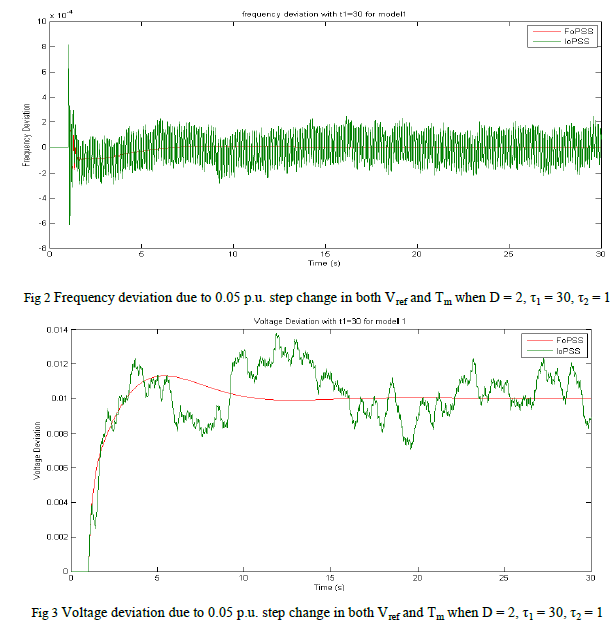
The maximum amount of phase needed depends on the fractional order of the FoPSS. Cascading more than one power system stabilizer would yield the amount of phase required to stabilize the system. The performance of the system is investigated using MATLAB/Simulink environment. It is assumed that the system with the exciter is working properly and a 0.05 p.u. step change in both ΔVref and Tm is applied to it at t=0.5s and t=2s, respectively. The IoPSS implemented is [3]:
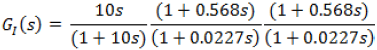image
For fractional-order controllers, two lead FoPSS is cascaded and followed by a limiter without a washout component to form a complete FoPSS controller
image
image

CONCLUSIONS
The FoPSS improved the performance of the infinite bus system and achieved a faster and smoother performance than its integer-order counterpart. Frequency and terminal voltage deviation over sever conditions were quickly absorbed when using FoPSS. FoPSSs has a larger bandwidth than its integer-order counterpart, and is expected to accommodate wider range of operating conditions. The increase in order in the case of FoPSS can be compensated by implementing already existing fast processors.

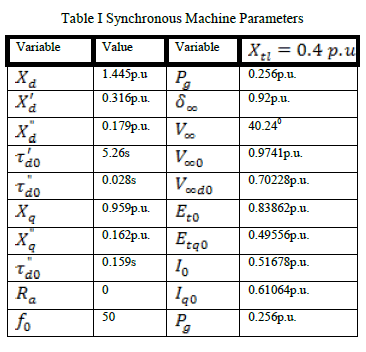
APPENDIX
Parameters for Model 2.1
image
image

ACKNOWLEDGMENT
First and foremost, I offer my gratitude to God Almighty for his blessings.
I express my heartfelt gratitude to our Principal Dr.M C Philipose, Saintgits College of Engineering, for providing the required facilities. I am grateful to my internal guides, Er.Haseena.K.A, Assistant Professor for their whole hearted support. I would also like to thank Associate Professor Er.Radhika.R for her innovative ideas. I hereby extend my sincere gratitude to all the staff members. Last, but not the least, I extend my sincere thanks to my family and friends for their valuable help and encouragement in my endeavor.
image
image

References
  1. R. El-Khazali, Z.A. Memon, and N. Tawalbeh, ‖Fractional-Order Power System Stabilizers‖, 4th-IFAC workshop on Fractional Differentiation and Applications, Badajoz, Spain 2010.
  2. R. El-Khazali, and N. Tawalbeh ―Multi-Machine Fractional-Order Power System Stabilizers‖ ,2012
  3. Anderson, P.M. and Fouad, A.A., Power System Control and Stability. New Jersy: IEEE Press, 1994
  4. Aboreshaid, S., and S. O. Faried,‖ Teaching Power System Dynamics and Control using SIMULINK‖, J. King Saud Univ., Vol. 12, Eng. Sci. (1), pp. 139-152, 2000
  5. Charef, A., Sun HH, Tsao YY, and Onaral B. ,‖Fractal system as represented by singularity function,‖ IEEE Trans. on Aut. Control 1992.
  6. Kundur, P. Power System Stability and Control. New York: McGraw-Hill, 1994.
  7. Larsen, E.V. and Swann, D.A., ―Applying Power System Stabilizers, Part I, II, III,‖ IEEE Trans. On Power Apparatus and Systems, PAS-100 No. 6, pp. 3017-3041, 1981.
  8. MITSUBISHI, ‖Power System Stabilizers,‖ http://www.meppi.com/Products/Generator%20Excitation%20Products%20Documents/Power%20System%20Stabilizer.pdf.
  9. Oldham, K. B. and J. Spanier, Fractional calculus, Academic Press, New York, 1974.
  10. Podlubny, I. Petras, B.M. Vinagre, P. O’Leary, and L. Dorcak, Analogue Realization of Fractional-Order Controllers,‖ Nonlinear Dynamics, Vol. 29, pp. 281-296, 2002.
  11. Saidy, M. and Hughes, F.M. ―Block diagram transfer function model of a generator including damper windings.‖ IEE Proceedings on Generation, Transmission and Distribution, 1994.