Reflection Coefficient Analysis Of Chebyshev
Impedance Matching Network Using
Different Algorithms

Rashmi Khare; Prof. Rajesh Nema

Reflection Coefficient Analysis Of Chebyshev Impedance Matching Network Using Different Algorithms

Rashmi Khare¹, Prof. Rajesh Nema²
Department of Electronics & Communication, NIIST/ R.G.P.V, Bhopal, M.P., India¹
Department of Electronics & Communication, NIIST/ R.G.P.V, Bhopal, M.P., India²

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology

Abstract

This paper discuss the design and implementation of broadband impedance matching network using chebyshev polynomial. The realization of 4-section impedance matching network using micro-strip lines each section made up of different materials is carried out. This paper discuss the analysis of reflection in 4-section chebyshev impedance matching network for different cases using MATLAB

Keywords

chebyshev polynomial , reflection, micro-strip line, matlab.

I. INTRODUCTION

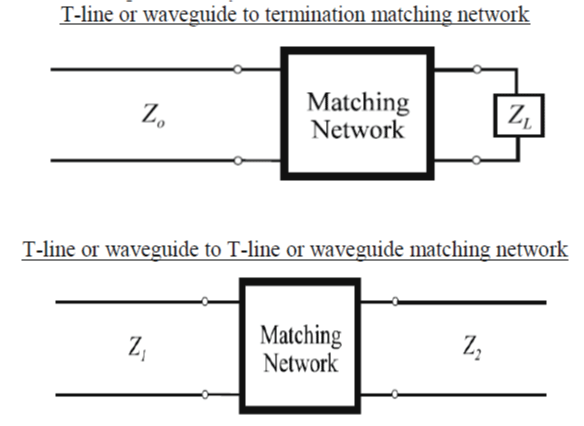
In many cases, loads and termination for transmission lines in practical will not have impedance equal to the characteristic impedance of the transmission line. This result in high reflections of wave transverse in the transmission line and correspondingly a high vswr due to standing wave formations, one method to overcome this is to introduce an arrangement of transmission line section or lumped elements between the mismatched transmission line and its termination/loads to eliminate standing wave reflection. This is called as impedance matching. Matching the source and load to the transmission line or waveguide in a general microwave network is necessary to deliver maximum power from the source to the load. In many cases, it is not possible to choose all impedances such that overall matched conditions result. These situations require that matching networks be used to eliminate reflections. Depending on the application, matching may be required over a band of frequencies such that the bandwidth of the matching network is an important design parameter. If the load impedance varies over a given range, a matching network which can be adjusted or tuned as necessary. In general, matching networks are constructed with reactive components only so that no loss is added to the overall network.

Impedance matching networks at a single frequency can be designed without much difficulty to provide a reflection coefficient of zero at the desired frequency. However, in many applications it is desirable to match impedances over a range of frequencies. One way of designing broadband matching networks is to use multiple sections of transmission line rather than just one section as in the case of the quarter wave transformer. In order to simplify the analysis of these multiple section matching networks, the theory of small reflections is utilized. A Chebyshev multi-section matching transformer can provide even larger bandwidths than a binomial multi-section matching transformer for a given number of transmission line sections. The increased bandwidth of the Chebyshev transformer comes at the cost of increased ripple over the pass-band of the matching network. However, we may still designate some maximum allowable reflection coefficient for the design of the Chebyshev transformer. The Chebyshev transformer exploits the characteristics of the Chebyshev polynomials.

II. LITERATURE SURVEY

NEW DESIGN TECHNIQUE OF N (Λ/4) SECTIONS IMPEDANCE TRANSFORMER USING GEOMETRIC INTERPOLATION.

This paper published in 2007 at SBMO/IEEE MTT-S International Microwave & Optoelectronics Conference (IMOC 2007). The proposal of this article is to present the new design technique of N (λ/4) sections impedance transformer using geometric interpolation. The article compares the Geometric Interpolation technique with Binomial and Chebyshev Models. The increase of bandwidth and the easiness of design are factors that distinguish this technique from others, making possible the use of this model in projects of wide band RF circuits and systems.

An exact synthesis method for dual-band chebyshev impedance transformers. This paper published in 2008 at Electromagnetics Research, PIER 86. This propose an exact synthesis method which allows the design of dual-band transformers with an arbitrary even number of uniform sections giving equi-ripple impedance matching in two separate bands centered at two arbitrary frequencies. This method is a generalization of the exact Collin- Riblet synthesis of Chebyshev single-band transformers. As compared to a single-band Collin-Riblet transformer encompassing both required pass-bands, the proposed design yields significantly better performance in terms of pass-band tolerance and width.

Design of multi-band multi-section transmission line transformer using particle swarm optimization.

This paper published in 2007 at springer. The design of Nt -section matching transformer operating at Nt arbitrary frequencies using the particle swarm optimization (PSO) method is presented. Although analytical methods based on standard transmission line theory can be used in such designs, however, the analysis becomes cumbersome if Nt exceeds two, and numerical methods should be used to solve the resulting nonlinear equations. The design using the PSO, however, is much easier, and gives the same results as the analytical methods. Different examples are presented and compared with published literature.

III. PROPOSED METHODOLOGY

In this work we reduced some parameters which affect the overall performance of chebyshev broadband impedance matching network. In these parameters include, reflection coefficient. Due to the reduction in above described parameters fractional bandwidth is increased. In this paper, we discuss the design and implementation of broadband matching network using chebyshev polynomial which is called chebyshev impedance matching network. The realization of 4-section impedance matching network using micro-strip lines each section made of different materials is carried out. Summarizing, the Chebyshev matching network design procedure is:

1. Determine the value N required to meet the

bandwidth and ripple Γm requirements.

This paper we analysed reflection coefficients characteristics in 4-section chebyshev impedance matching network where each section is made up of different materials like alumina, RT/duroid, FR-4, Teflon. We described these analysis for different width cases and different material combinations, and for that we used different algorithm like wheeler, yamashita, krischning and jansen, kobayashi given by various researchers for micro-strip lines which provides the value of εeff(f) i.e. frequency dependent effective micro-strip permittivity. This value of εeff(f) is used to calculate the characteristic impedance of each section of micro-strip lines made up of different materials and then compare the results using matlab simulator.

For wheeler:

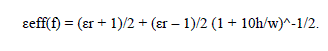For yamashita:

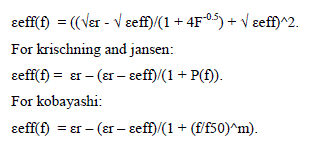We will describe the analysis using three cases:

CASE 1: When the width of each sections are in increasing order i.e. w1 = 0.1cm, w2 = 0.2cm, w3 = 0.3cm, w4 = 0.4cm, respectively and height of each section is h = .15cm and load impedance Zl = 60Ω and ripple Γm = 0.2.

CASE 2: When the width of each sections are same i.e. w1 = w2 = w3 = w4 = 0.25cm, and height of each section is h = .15cm and load impedance Zl = 60Ω and ripple Γm = 0.2.

CASE 3: When the width of each sections are in decreasing order i.e. w1 = 0.4cm, w2 = 0.3cm, w3 = 0.2cm, w4 = 0.1cm, respectively and height of each section is h = .15cm and load impedance Zl = 60Ω and ripple Γm = 0.2.

for As each section is made up of different materials like alumina, RT/duroid, FR-4, Teflon so there are twenty four combinations of four sections and we are taking four different algorithm like wheeler, yamashita, krischning and jansen, kobayashi so for above three cases we will optimize which material combination and Which algorithm is resulting less reflection coefficient, for that we will observe all twenty four combinations applying all four algorithms in each case.

IV. RESULTS AND DISCUSSION

• According to the figures1,2 and 3 we can clearly see that among the four algorithms wheeler is better because it gives less reflection then others and kirstchining and jansen algorithm provides almost same result as wheeler.

• In the above given table.1 it is clearly shown that ARFT material combination gives less reflection using different algorithms for different cases.

V.CONCLUSION

In this paper, we create a 4- section chebyshev matching network using where each section is made of different materials then we calculate the reflection using different algorithms and different width cases then we conclude that ARFT combination is good for case1 using wheeler algorithm.

Tables at a glance

Table 1

Figures at a glance


Figure 1	Figure 2	Figure 3

References

C. N. M. Marins, School of Electrical and Computer Engineering, State University of Campinas, SP, Brazil,and L. A. Beraldo INATEL – National Institute of Telecommunications, Santa Rita do Sapucai, MG, Brazil, “New Design Technique of N (λ/4) Sections Impedance Transformer using Geometric Interpolation”, 2007 SBMO/IEEE MTT-S International Microwave & Optoelectronics Conference (IMOC 2007).
Majid Khodier, Nihad Dib, Jehad Ababneh, Electrical Engineering Department, Jordan University of Science and Technology,” Design of multi-band multisection transmission line transformer using particle swarm optimization”, Received: 30 August 2006 / Accepted: 8 June 2007 / Published online: 4 July 2007© Springer-Verlag 2007.
Jim Stiles, The university of Kansas, Department of EECS, "The Chebyshev Matching Transformer",2010.
KC Gupta, Indian Institute Of Technology, Kanpur, ”Microwaves”.
Tables of Chebyshev Impedance-Transforming Networks of Low-Pass Filter Form, GEORGE L. MATTHAEI, MEMBER, LEEE
Wu, G.-L., W. Mu, X.-W. Dai, and Y.-C. Jiao, ?Design of novel Dual band band-pass filter with microstrip meander loop resonator CSRR DGC,? Progress in Electromagnetic research, PIER 78,17-24, 2008.
Ren, W., ?Compact dual-band slot antenna for 2.4/5 GHz WLAN applications,? Progress In Electromagnetics Research B, Vol. 8, 319-327, 2008.
Fan, J.-W., C.-H. Liang, and X.-W. Dai, ?Design of cross-coupled Dual band filter with equal length split ring resonator,? Progress in Electromagnetic Research ,PIER 75,285-293, 2007.
Zhao, G., F.-S. Zhang, Y. Song, Z.-B. Weng, and Y.-C. Jiao, ?Compact ring monopole antenna with double mender lines for 2.45/5 GHz dual-band operation,? Progress In Electromagnetic Research, PIER 72, 187-194, 2007.
Chow, Y. L. and K. L. Wan, ?A transformer of one-third.
W. Bakalski, W. Simbürger, H. Knapp, H. Wohlmuth, and A. L. Scholth, ?Lumped and distributed lattice-type LC-baluns,? in IEEE . MTT-S Int. Microwave Symp. Digest, 2002, pp 209–212.
D. Kuylenstierna and P. Linner, ?Broadband lumped element baluns with inherent impedance transformation,? IEEE Trans Microw. Theory Tech., vol. 52, pp. 2739–2745, Dec. 2004.
S.Horst, R.Bairavasubramanian, M.M. Tentzeris, J.Papapolymerou, ?Modified Wilkinson Power Dividers for Millimeter-Wave Integrated Circuits,? IEEE Trans. Microw. Theory Tech., vol.55, no. 11, pp.2439-2446, Nov. 2007.