Reliability-Security Constrained
Unit Commitment with Hybrid Optimization
Method

Ahmad Heidari; Mohammad Reza Alizadeh Pahlavani; Hamid Dehghani

Reliability-Security Constrained Unit Commitment with Hybrid Optimization Method

Ahmad Heidari¹, Mohammad Reza Alizadeh Pahlavani², Hamid Dehghani³
Malek-Ashtar University of Technology (MUT), Shabanlo St., Lavizan, Tehran, Iran

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

This paper presents an advanced optimization technique to solve unit commitment problems and reliability issues simultaneously for thermal generating units. To solve unit commitment, generalized benders decomposition along with genetic algorithm to include minimum up/down time constraints are proposed, and for reliability issues consideration, a fuzzy stochastic-based technique is presented. To implement the problem into an optimization program, the MATLAB® software, and CPLEX® and KNITRO® solvers are used. To verify the proposed technique and algorithm, two case studies that are IEEE 14 and 118 bus systems are implemented for optimal generation scheduling, and reliability issues. Finally, a comparison with other solution techniques has been given.

Keywords

Benders Decomposition, Fuzzy Programming, Genetic Algorithm, Optimization technique, Reliability Issues, Unit Commitment.

INTRODUCTION

Reliability-constrained unit commitment (RCUC) is applied to minimize the costs economically, and schedules unit reserves like spinning reserves to provide system reliability; On the other hand, loss of load probability must be taken into consideration to obtain customers satisfactory of the power system. A lot of optimization methods and modelling techniques are proposed to solve security-constrained unit commitment (SCUC) [1-5]. In [6] unit commitment solution is considered based on uncertainty, and a combination of benders decomposition and the outer approximation technique is proposed. In [7] unit commitment solution is developed with integrating of wind power and demand response uncertainties with aid of benders decomposition. In [8], multi-objective unit commitment with fuzzy membership design variables is tuned. In [9], unit commitment and reliability are proposed under uncertain forecasting based on fuzzy credibility theory. In [10], unified stochastic and robust unit commitment problem along with reliability is developed based on benders decomposition algorithm. In [11], a benders decomposition approach is proposed for a combined heat and power system. In [12], a fuzzy radial interval linear programming model is developed for robust planning of energy management systems with environmental consideration. In [13], security-constrained selfscheduling of generating companies in day-ahead electricity markets is considered.

Among these techniques and methods, Benders decomposition [14-16] is applied more because of the nature of the power system problems which is mixed integer; like on/off state of generating units. Benders decomposition is a decomposition technique separating the main problem and subproblem such that solving the whole problem needs less computation burden. In this paper, in master problem, the minimum up and down time constraints are nonlinear [17], and may lower program speed; therefore, a modified genetic algorithm is used to just solve these constraints.

Based on [1, 18-20] genetic algorithms (GAs) are adaptive search methods that obtain their characteristics from the genetic processes of biological organisms based on evolution facts.

In power system operations, there are two other methods for distributing energy and system reserves; that is, sequential dispatch and simultaneous dispatch [21]. As [21] proposes, the better solution of the problem from optimization viewpoint is found when all the constraints and limitations are considered simultaneously rather than sequentially. [22]

Proposes a mixed deterministic-probabilistic structure to the system reserves with market-clearing algorithm and UC. However, [22] just runs the algorithm for one time period. Other references like [21] and [23] consider system reserves like interruptible loads.

For reliability issues, loss of load probability (LOLP) along with system spinning reserves are included, and because of the nature of the problem that is stochastic based, a fuzzy algorithm is implemented to consider the stochastic nature of reliability issues.

With review of literature, the gap needs to be filled with a robust and advanced optimization technique. This proposes a technique solving SCUC problem and Reliability issues simultaneously with aid of existing and advanced optimization techniques having less computation burden, yielding robust, reliable and comparable with other results.

The main contribution of this paper is to use some existing optimization techniques that are benders decomposition, genetic algorithm, and fuzzy programming all together to solve a problem that is not only based on unit commitment, but also is based on reliability issues, and includes to study two necessary parts of power system. It is noted that in this definition, reliability issues are considered as spinning reserves, and the ability of power system under study to supply loads (LOLP).

The reason why authors were specific on these methods those are Generalized Benders Decomposition (GBD), Genetic Algorithm (GA), and Fuzzy Programming (FP) was that they have the ability to tackle with these kinds of problems based on the literature; so, the authors made a decision to optimize these methods based on new challenge for each part of the problem separately and altogether.

The advantage of these methods is searching and finding a feasible solution matching with the proposed algorithm, and decreasing computational burden. In other words, these methods have a good convergence based on the size of the given problem.

The rest of the paper is organized as follows:

Section 2 proposes formulation and methodology. Section 3 gives two case studies that are IEEE 14 and 118 bus systems to verify the proposed technique, and finally Section 4 concludes the remarks.

FORMULATION AND METHODOLOGY

A. Security-Constrained Unit Commitment and Reliability Issues Formulation

To formulate Security Constrained Unit Commitment (SCUC) and reliability issues mathematically, the constraints and formulations are as follows:

Power balance, Minimum up and down time constraints, Ramp rate limits, unit reserves, loss of load probability (LOLP), startup cost, and shutdown cost.

In this paper, the whole problem is a mixed integer nonlinear program (MINLP) problem, and is solved with Generalized Benders Decomposition method along with considering minimum up and down time constraints applying genetic algorithm. In this technique, unit commitment (UC) is master problem assigning on/off state of generating units; at the next step, subproblem solves economic dispatch (ED), and finally reliability issues are solved applying fuzzy programming.

All formulations and constraints are as follows [23-27]:

Power Balance:

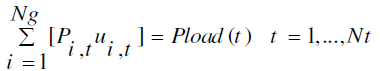Eq. (1) indicates that each running generating unit must supply the active power demanded by the loads at each specified hour.

Limits of generating units:

Eq. (2) indicates that because of physical properties of turbine and generating units, the supplied active power must be between min and max values.

Minimum up/down Time constraints:

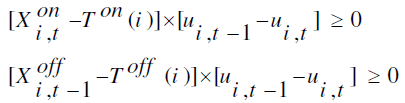Eq. (3) defines minimum up/down time constraints. Minimum up time is defined as once the unit is running; it should not be turned off immediately. Minimum down time is defined as once the unit is decommited; there is a minimum time before it can be recommitted. In above eqs., Ton and Toff are minimum up time and minimum down time of unit i respectively, and Xon and Xoff are ON time and OFF time of unit i at time t before beginning of the specified time. It means that X depends on elapsed time the generating units were running.

Ramp-up Rate Limits:

In eq. (4), the traditional model for ramping is considered; that is, the ramp rates are fixed at all loading levels and the ramping delay is not considered.

Inequality of generating units’ active Power:

Eq. (5) is a mathematical constraint.

Objective function of minimization problem for SCUC is:

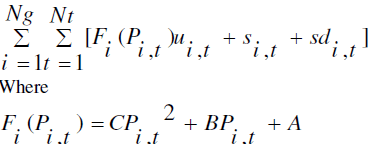Eq. (6) defines the objective function of the operational part of programming. It includes three sums; the fuel cost depending on nonlinear curve namely F (P), startup cost, and shut down cost.

In equations (1) to (6), i and t are indices standing for generating units and time period, respectively. P is active power of generating units, Pload is consumed active power at load buses, Rup is ramp-up rate limit, s represents startup cost, sd represents shutdown cost, and u is a binary value assigning on/off states of generating units. A, B, and C are constants applying for cost functions of fuels for generating units.

All information and formulation of reliability issues are as follows:

Spinning Reserves Limits [21-22]

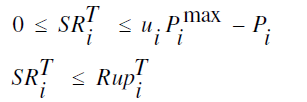Eq. (7) indicates the spinning reserve of generating units, and that is the ability of generating units to supply for reliability issues when generating units cannot supply loads normally. In this Eq., SR represents spinning reserves in MW.

To consider LOLP that is a constraint and it must be satisfied in reliability issues part of the problem: LOLP can be defined classically as [22]:

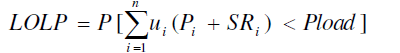In other words, LOLP is the probability (P) that the available generation, including spinning reserve, cannot meet the system load for all generating units.

Finally, objective function of reliability section is added to the equation (6).

In Eq. (11), PSR is the cost for each MW produced in money unit. It is noted that LOLP is an obligatory constraint, and it must be satisfied for the problem to be solved.

B. Algorithm

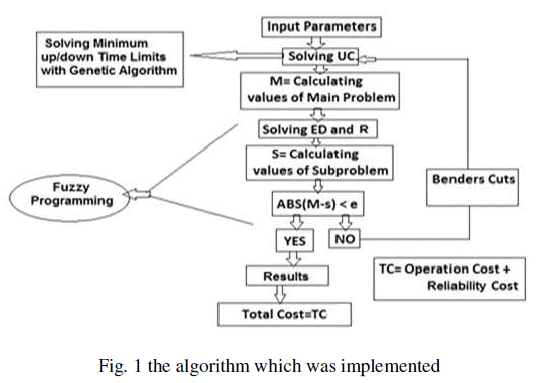
The algorithm which is implemented in this paper is depicted in Figure 1. The algorithm is based on a mixed optimization technique that solves the running program in each iteration. As depicted, at first step, generalized benders decomposition (GBD) solves unit commitment while genetic algorithms help solve the nonlinear part of problem that is minimum up and down time constraints. After finding minimum cost of operational section, fuzzy programming based on a stochastic method is called to solve the rest of the program that is reliability issues part of the program. In each iteration, fuzzy programming and genetic algorithm work under support of benders decomposition until an absolute minimum point is found yielding minimum cost of power system, and satisfying reliability issues constraints.

The reason why these mixed optimization techniques are applied returns to the structure that the program deals with it, and that is structural properties of power system under study; it means, being mixed integer (generalized benders decomposition), nonlinear (genetic algorithms), and probabilistic structure (fuzzy programming).

As shown, TC standing for Total Cost of power system is sum of operational cost that relates to unit commitment and Reliability issues cost.

As shown in Figure 1, R stands for reliability functions and the running program stops if and only if absolute value of master problem and subproblem is less than a pre-specified tolerance. The equations that link master problems and subproblems constraints are benders cut that are equations when NO box in Figure is obtained.

Main advantage of the proposed algorithm is its ability to take care of unit commitment problem that is a traditional problem, and reliability issues constraints that are less traditional ones into a modern and advanced optimization techniques that has some properties: applying several optimization methods in spite of just one optimization program that may have some deficits; less computational burden; applying stochastic properties of fuzzy programming, and evolutionary properties of genetic algorithm under support of generalized benders decomposition that is a robust optimization program.

C. Optimization Program

C.1 Generalized Benders Decomposition (GBD)

GBD problem is as follows [14]:

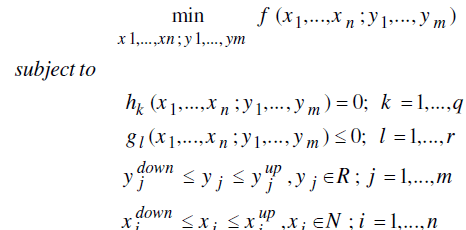In (10), xi are integer parameters and yj are non-integer parameters. hk defines equalities and gl defines inequalities. f is objective function of optimization problem. Note that upper and lower bounds are imposed on optimization variables to reflect physical limits.

In the method applied in this paper, the program written by the authors in MATLAB® applies a branch and cut method [14] to obtain a feasible solution based on cutting the extra space searching the desired minimum or maximum point. The property of this method is its iteration: if there is no feasible solution at first iteration, with aid of benders cut, it loops for the second iteration, and so on until searching and finding minimized or maximized objective function. It is noted that Genetic Algorithm and Fuzzy Programming are subsets of GBD, and run under main program.

C.2 Fuzzy Programming (FP)

A simple way of converting a stochastic model to a deterministic model using fuzzy set theory is to take its expected value:

F = E (Reliability Constraint s )

Where E is expected value

Putting reliability constraints together:

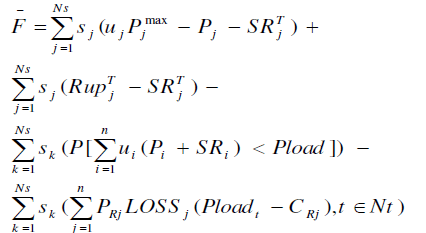In above equation, si are slack variables, i, j, and k are indices, and F defines objective function of the reliability constraints. As written, equations of reliability section are applied. Eq. (12) is based on eqs. (7, 8 and 9). The authors applied “Fuzzy Logic” toolbox of MATLAB® applying FIS editor based on eqs. (11 and 12). First of all, eq. (14) has been linearized, and state variables were picked as desired reliability parameters that are Spinning Reserve (SR) and LOLP. It is noted that limitations of these parameters have been given in eqs. (7, 8, and 9), and as Genetic Algorithm, Fuzzy Programming is part of outer optimization program, and is in a loop. On the other hand, capacity outage probability table (COPT) was formed using the data given.

The method applied for this part of problem was “mamdani”, and defuzzification method was “centroid”. Fuzzy set was considered as [NB NS ZR PS PB] standing for negative big, negative small, zero, and positive small and positive big, respectively. Membership function was considered as triangle.

C.3 Genetic Algorithm (GA)

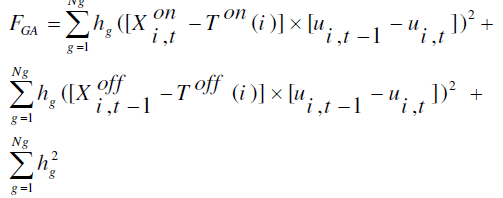hg are slack variables, g is index for integer binary parameters, and FGA is objective function of this part of problem. GA is designed for the solution of maximization problem, so the fitness function is defined as the inverse of equation (13):

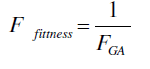It is noted that genetic algorithm doesn’t solve the objective function solely, and it is a subset of an outer optimization program.

As eqs. (13, 14) proposes, GA converts minimum up/down time constraints to an objective function, and searching fitness function with inverting of objective function. To solve this part of problem, an m-file was written based on “Genetic Algorithm and Direct Search” toolbox of MATLAB®.

Finally, GA and FP are converted to two separate m-files; each m-file is called in a module by the m-file written by the GBD.

RESULTS AND DISCUSSIONS

In this section, two case studies, IEEE 14 and 118 bus test systems were implemented to verify the proposed algorithm for a multi-period optimization problem. Master problem is a Mixed Integer Programming (MIP) problem along with genetic algorithm applying CPLEX solver, and Subproblem is an MINLP problem and fuzzy stochastic based problem applying KNITRO solver. The proposed method was implemented on a DELL VOSTRO 1320 with an Intel (R) Core (TM) 2 Duo CPU 2.53 GHz and 4 GB RAM using MATLAB® programming file (m-files®), and MATLAB toolboxes for fuzzy programming and genetic algorithm.

A.IEEE 14 bus system

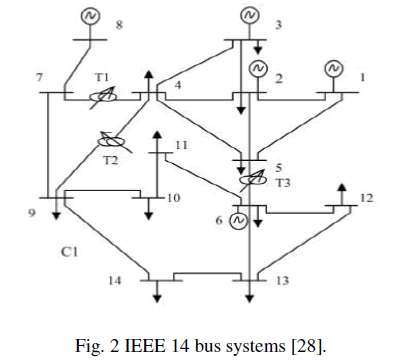
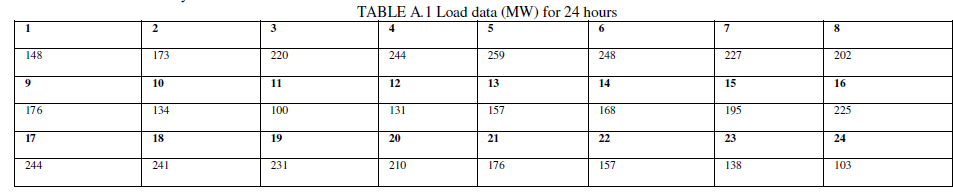
Figure 2 depicts the IEEE 14 bus system [28]. As shown in figure 2, this system has five generating units at buses 1, 2, 3, 6, and 8. There are three tap-changing transformers named T1, T2, and T3. All data for loads and generating units are in appendix-A.

A.1 UC Results

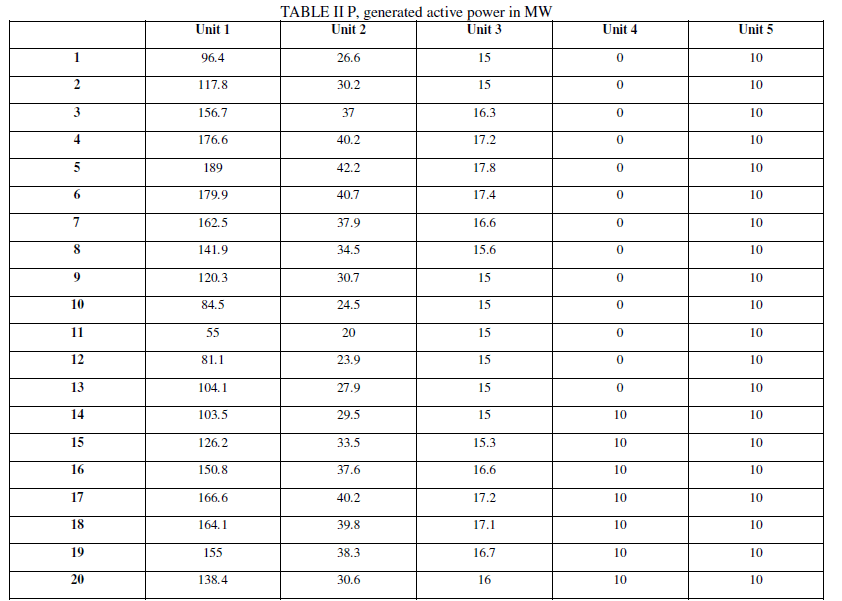
Running the optimization program yields on/off state of generating units, u, and P, active generated power in MW. Tables 1 and 2 show data obtained from algorithm.

As shown in tables 1 and 2, unit 1, the cheapest generating unit, generates all 24 hours. Unit 2, the next cheapest unit, generates 23 hours with respect to minimum up and down time constraints. It is noted that all the constraints have been satisfied. Genetic algorithm satisfies the nonlinear constraint, minimum up and down time constraints. Minimum power and maximum power have been satisfied, and the minimum cost is obtained.

Number of iterations for this part of case study is 3, and time elapsed is 1.5240 s that 0.9872 s spends in genetic algorithm loop.

Minimum Operational cost with respect to eq. (6) including startup and shut down cost is 11149 in money unit.

A.2 Reliability Issues Results

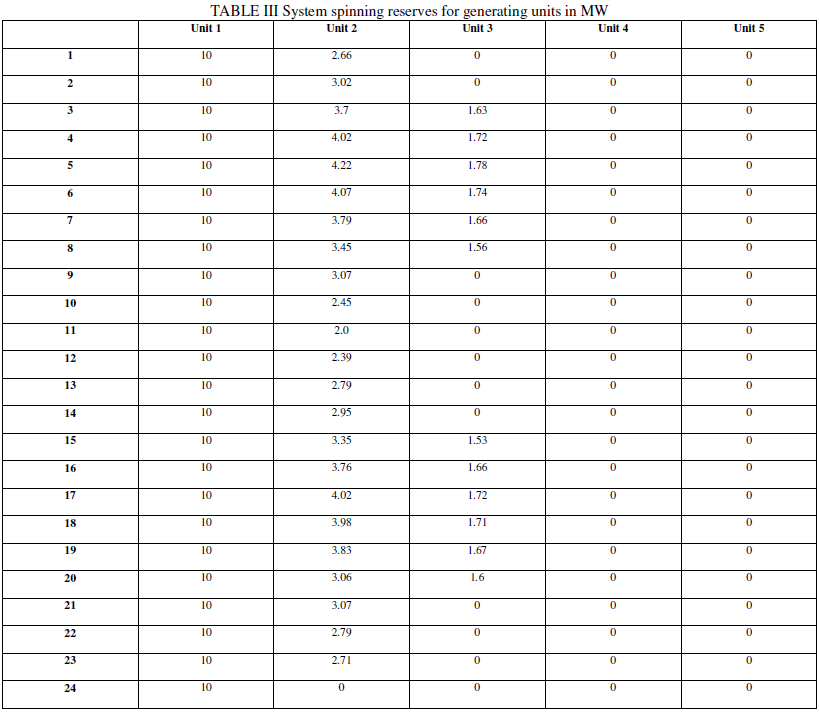
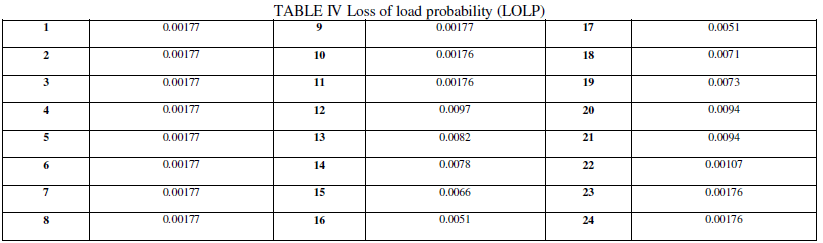
For reliability issues, two variables including system spinning reserves (SR) and LOLP are obtained. Tables 3 and 4 show data obtained from conducted program.

As shown in tables 3 and 4, LOLP that is a constraint was satisfied. System reserves also helps the generating units be able to satisfy system reliability.

Number of iterations for this part of case study is 7, and time elapsed is 3.3250 s. this results were obvious because of time-consuming properties of fuzzy programming.

Finally, the total cost from eq. (11) is (that is, sum of reliability cost and operational cost): 11183.08 in money unit.

B.IEEE 118 bus system

The IEEE-118 bus test system has 54 thermal generators, 186 branches, and 91 demand sides. The parameters of generators, transmission network, and load profiles are given at http://www.ee.washington.edu/research/pstca/pf118/pg_tca118fig.htm.

B.1 UC Results

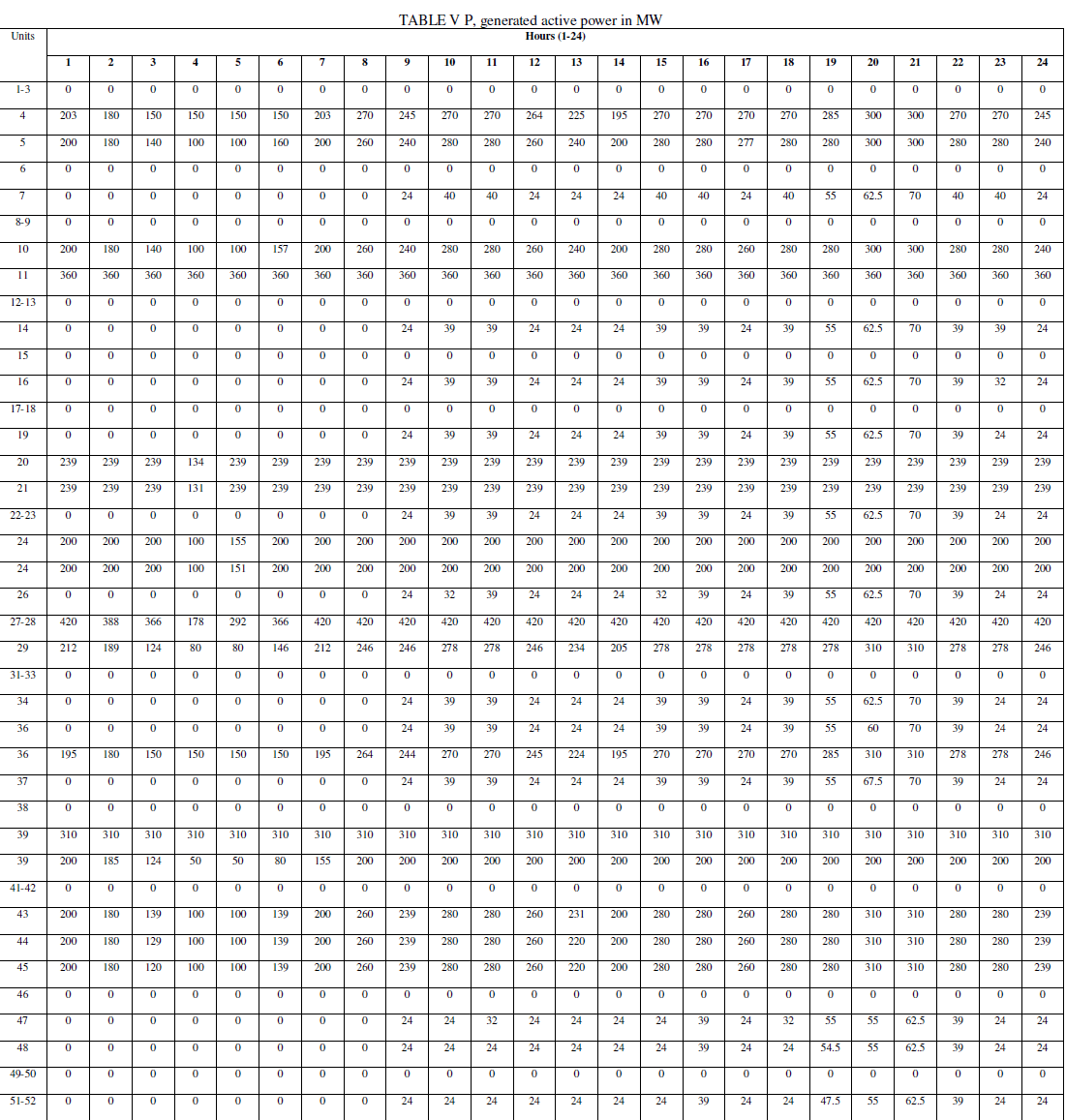
Conducting another optimization program for IEEE 118 bus test system gives P, generated active power in MW. Table 5 shows data obtained from algorithm.

As shown in table 5, it should be noted that all the constraints have been satisfied. Genetic algorithm satisfies the nonlinear constraints, minimum up and down time constraints. Minimum power and maximum power have been satisfied, and the minimum cost is obtained.

Operational cost with respect to eq. (6) including startup and shut down cost is 1,643,818 in money unit.

B.2 Reliability Issues Results

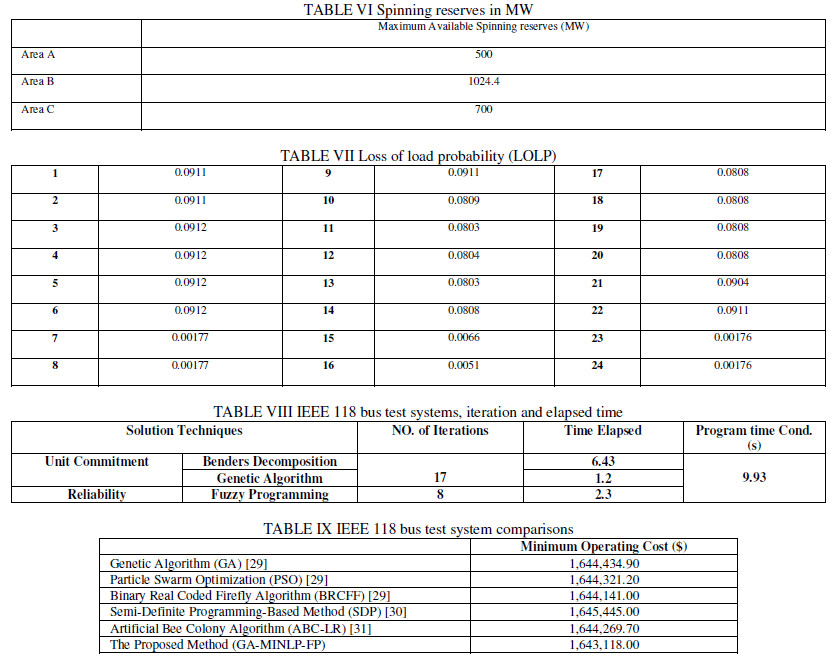
For reliability issues, two variables including system reserves and LOLP are obtained. Tables 6 and 7 show data obtained from conducted program.

As table 6 shows, for spinning reserves studies, the IEEE 118 bus test system has been converted to 3 zones [29]: A, B and C. Zone A includes left side of the figure, Zone B includes bottom side, and zone C includes top side. The blow table shows results:

As shown in table 7, LOLP that is a constraint was satisfied.

Finally, the total cost from eq. (11) is (namely, sum of reliability cost and operational cost): 1,644,039.44 in money unit.

TABLE 8 shows NO. Iterations and time elapsed to conduct IEEE 118 bus system.

C. Comparison with other solution techniques

In this section, the results obtained with the proposed algorithm have been compared with other algorithms and optimization programs to verify the results. Table 9 shows the results.

It should be noted that TABLE 9 just includes unit commitment problem, and the cost of considering reliability issues must be added to this operating cost.

CONCLUSION

In this paper, optimal generation scheduling in two power systems that are IEEE 14 and 118 bus systems was implemented for both security-constrained unit commitment (SCUC) and reliability issues for 24 time period horizon. This implementation applied an advanced and mixed optimization technique including generalized benders decomposition, genetic algorithm, and fuzzy programming. SCUC problem and the reliability issues constraints were considered simultaneously. The results obtained from the case studies presented good convergence with the proposed algorithm, and in comparison with other solution techniques, the proposed method shows the superiority. The paper proposes to satisfy system reliability issues and economy simultaneously, some extra costs must be paid. It also proposes that this advanced optimization technique is a suitable technique to address this kind of power system problems as well as lowering computational burden.

References

Zhu, J.,“Optimization of power system operation”. New Jersey, Wiley & Sons, Inc., p. 251, 2009.
Daneshi, H., Jahromi, A. N., Li, Z. andShahidehpour, M. “Fuzzy mixed-integer programming: approach to security-constrained unit commitment”.IEEE. Power & Energy Society General Meeting. PES '09: IEEE. pp. 1-6., 2009.
Guan, X., Guo, S. andZhai, Q.,“The conditions for obtaining feasible solutions to security-constrained unit commitment problems”. IEEE Trans. Power Syst.; 20: 1746–1756., 2005.
Wu. L., Shahidehpour., M. and Tao., L.,“Stochastic security-constrained unit commitment”. IEEE Trans. Power Syst.; 22: 800-811., 2007.
Geoffrion, A. M.,“Generalized benders decomposition”. J. Optim Theory Appl.; 10: 237–261., 1972.
Bertsimas, D., Litvinov., E., Sun., X. A., Jinye., Z. andTongxin., Z.,“Adaptive robust optimization for the security constraint unit commitment problem”. IEEE Transaction on Power Systems; 28: 52-63., 2013.
Zhao., C., Wang., J., Watson., P. J. and Guan., Y., ” Multi-stage robust unit commitment considering wind and demand response uncertainties”. IEEE Transaction on Power Systems; 28: 2708-2717., 2013.
Chandrasekaran., K. and Simon., S. P.,“Optimal deviation based firefly algorithm tuned fuzzy design for multi-objective UCP”. IEEE Transaction on Power Systems; 28: 460-471., 2013.
Wang., B., Li., Y. andWatada., J.,“Supply reliability and generation cost analysis due to load forecast uncertainty in unit commitment problems”. IEEE Transaction on Power Systems; 28: 2242-2252., 2013.
Zhao., C. and Guan., Y.,“Unified stochastic and robust unit commitment”. IEEE Transaction on Power Systems; 28: 3353-3361., 2013.
Abdolmahammadi., H. R. andKazemi., A. A.“Benders decomposition approach for a combined heat and power economic dispatch”. Elsevier, Energy Conversion and Management; 71: 21-31.,2013.
Donga., C., Huang., G. H., Cai., Y. P. and Liu., Y. “Robust planning of energy management systems with environmental and constraintconservative considerations under multiple uncertainties”. Elsevier, Energy Conversion and Management; 65: 471-486.,2013.
Amjadi., N. andVahidinasab., V. “Security-constrained self-scheduling of generation companies in day-ahead electricity markets considering financial risk”. Elsevier, Energy Conversion and Management; 65: 164-172.,2013.
Conejo., A. J., Castillo., E., Minguez., R. and Garcia-Bertrand., R. “Decomposition techniques in mathematical programming, engineering and science applications”. Springer, Netherlands. p.251.,2006.
Laothumyingyong., N. andDamrongkulkamjorn., P. “Security-constrained unit commitment using mixed integer programming with benders decomposition”. IEEE, International Conference on Electrical Engineering/Electronics Computer, Telecommunications and Information Technology (ECTI-CON), pp. 626-631., 2010.
Cvijic., S. andJinjun., X. “Security constrained unit commitment and economic dispatch through benders decomposition: a comparative study”. IEEE, Power and Energy society General Meeting, pp. 1-8., 2011.
Carrion., M. and Arroyo., J. M. “A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem”. IEEE Transactions on Power Systems; 21: 1371-1378., 2006.
Maifeld., T. T. andSheble., G. B. “Genetic-based unit commitment algorithm”. IEEE Transactions on Power systems; 11: 1369-1370., 1996.
Belegundu., A. D. andChandrupatla., T. R.“Optimization concepts and applications in engineering”. 2nd ed. Cambridge University Press, pp. 318-324., 2011.
Reeves., C. R. andRowe., J. E. “Genetic algorithms- principles and respective- a guide to GA theory”. New York, NY, USA: Kluwer Academic Publishers, 2002.
Aminifar., F. andFotuhi-Firuzabad., M. “Reliability-constrained unit commitment considering interruptible load participation”. Iranian Journal of Electrical & Electronic Engineering; 28: 10-20., 2007.
Bouffard., F. andGaliana., F. “An electricity market with a Probabilistic spinning reserve criterion”, IEEE Trans. Power Systems; 19: 310–317., 2004.
Aminifar., F., Fotuhi-Firuzabad., M andShahidehpour., M. “Unit commitment with probabilistic spinning reserve and interruptible load consideration”. IEEE Trans. Power System; 24: 388-397., 2009.
Fu., Y., Shahidehpour., M. and Li., Z. “Security-constrained unit Commitment with AC constraints”, IEEE Trans. Power Syst.;20:1538–1550., 2005.
Shahidehpour., M., Yamin. and H., Li., Z. “Market operations in electric power systems: forecasting, scheduling, and risk management”. New York, NY, USA: IEEE, Inc, A John Wiley & Sons, Inc., Publication, 2002.
Padhy., N. P. “Unit commitment-a bibliographical survey”. IEEE Trans. Power System; 19: 1196-1205.,2004.
Wood., A. J. andWollenberg., B. F. “Power generation, operation, and control”, 2nd ed., New york, NY, USA: A John Wiley & Sons, Inc., Publication, 1996.
Lotfju., A., Shahidehpour., M., Fu., Y. and Li., Z. “Security-constrained unit commitment with AC/DC transmission systems”. IEEE TRANSACTIONS ON POWER SYSTEMS; 25: 531-542., 2010.
Chandrasekaran., K. andSimon., S. P. “Optimal deviation based firefly algorithm tuned fuzzy design for multi-objective UCP”. IEEE TRANSACTIONS ON POWER SYSTEMS 2013; 28: 460-471.
Bai., X. andWei., H. “Semi-definite programming-based method for security-constrained unit commitment with operational and optimal power flow constraints”. IET Gen., Transm, Distrib.;3: 182–197., 2009.
Chandrasekaran., K., Hemamalini., S., Simon., S. P. andPadhy., N. P. “Thermal unit commitment using binary/real coded artificial bee colony algorithm”. Elect. Power Syst. Res.; 84: 109–119., 2009.