International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
MenuISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
M. Nagaraju Naik1, Dr. P. Rajesh Kumar2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
The problem of resolution projection based on the approach of compression sensing is developed. For a fast and accurate processing of resolution projection compression sensing based coding is followed. In such approach a sparse based modeling is used for the interpolation of frame samples. wherein sparse provide a higher speed of processing the problem of optimal convergence of these matrix exist. To overcome the limitation of sparse matrix, in this paper a new approach to projection based on circulant matrix is proposed. The usage of such matrix results in the minimization of computation time, retaining processing accuracy. For the evaluation of the proposed approach an enhanced method called I-OMP is considered. The comparative analysis of this approach is found to be more effective by the usage of this circulant matrix resulting in faster and accurate processing.
Keywords |
| Resolution projection, circulant matrix, sparse coding, compressive sensing. |
INTRODUCTION |
| The objective of image interpolation [2] is to obtain high resolution images from low resolution inputs. It is widely applicable in video communication, object recognition, HDTV, image compression, etc. The generation process of low resolution images can be modeled as a combination of smoothing and down-sampling operations of the natural scenes by low quality sensors. Super resolution is an inverse problem of this generation process, so it is under-determined due to the information loss. One criteria of solving this inverse problem is minimizing the reconstruction error. Various methods were proposed in the literature to regularize the inverse problem. Two of the most extensively explored image modeling approach is the image smoothness approach and the edge smoothness approach. Simple filtering/interpolation algorithms (e.g., bilinear/bicubic interpolation) can produce smooth high resolution images, which are usually blurry, thus have limited image quality. To preserve edge sharpness, edge directed interpolation [3, 4] is proposed to prevent cross-edge interpolation. However, locating high precision edge position itself is a non-trivial task. Level-set [5] and multiple scale tensor voting [6] methods are explored to get smooth edges. Edge preserving smoothness prior on large neighborhood is proposed in [7]. In [8], a soft edge smoothness term which can measure the average length of discrete level lines is incorporated into an objective function to produce smooth soft edges. Methods based on image modeling are more efficient. One critical issue is how to handle image edges in a satisfactory way. Simple interpolation strategies tend to produce blurry results, while edge preserving methods may remove image details in regions without strong edges. Where in a back propagation approach [1] was been proposed, the error coding at the edge preservation was not achieved, and the ringing artifacts are observed more dominant. In super resolution, the reconstruction of SR image is equivalent to how to construct measurement matrix and design reconstruction algorithm. As the OMP method for super resolution is almost efficient algorithm for image reconstruction, the number of measurements that required for reconstruction is the least. However, for large image reconstruction, a great number of high dimensional projection computations are required, which will affect the computation time for reconstruction of an image [9]. [10] Proposed an image reconstruction Improved-OMP (IOMP) algorithm based on the sparse projection matrix under the consideration of computation time. But the problem associated with the method, there is no that much efficient reduction in the computation time. So In this paper to achieve the objective of efficient image projection with less computation time a Circulant matrix based image projection technique is proposed along with the integration of circulant- IOMP algorithm. |
| The rest of the paper is organized as follows: section II The sparse projection based IOMP method used to reconstruct an image is illustrated in section III. gives the proposed Topleiz and Circulate projection matrix based image reconstruction algorithm with the aim of less computation time. The performance evaluation of the proposed method is represented in section IV. Finally conclusions are made in the section V. |
SPARSE PROJECTION MATRIX |
| In order to reconstruct the image one need to construct the random measurement matrix from the information of the original image with less measurement time. In order to ensure the original structure of the image, the measurement matrix should satisfy the isometric properties proposed in [6]. With the given restricted properties two measurement matrixes generated. 1. Gaussian random measurement represented by eqn.(1) and the 2. Bernoullis measurement matrix and is described by eqn. (2). |
 |
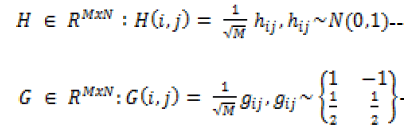| An image can be rebuild by using the above two matrices considering certain measurement points. For large images, in order to rebuild it requires high computations in turn it will effect the reconstruction speed. So as to enhance the speed and the image reconstruction quality. The measurement matrix is enhanced by two factors which will help in assuring the reconstruction speed 1. Finding new measurement matrix with less number of measurements, (2) for simplified computation the new matrix measurement should follow the properties of sparsity for high dimensional data. The new measurement matrix with sparse properties is called as sparse random projection matrix which helps in enhances of speed with less projection computations. |
| The sparse projection matrix is obtained by using two random variables with the following distribution |
 |
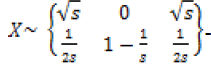| If 1≤s≤3 then the X obeys sparse distribution matrix which means that, when s=3, only 1/3 of original data are sampled. Based on the sparse elements of the sparse projection, during reconstruction of the image the speed of the sparse random projection is increased by 3 times. From the [10] the sparse projection matrix is given the following formulae Where H is a Gaussian random matrix and is any random variables which obey Gaussian distribution. Assuming , for any , we obtain the below formulae: |
 |
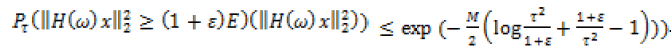CIRCULANT MEASUREMENT MATRIX |
| By using the sparse projection matrix the reconstruction image of high resolution is much better than the interpolation methods. Image reconstruction is enhanced by sparse projection matrix, but not better enough as the optimal sparse is not calculated by choosing the measurement points for reconstruction of the image which is not concern in this paper. So as to enhance the speed of reconstruction image with less computation in this paper we a proposing a circulant measurement matrix is given by the following eqn. (5) |
 |
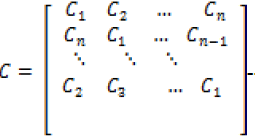| Whose ith row is formed by i-1 times’ circulant shifting its first row as described in equation (5). |
| In computational complexity the Circulant measurement matrix has good properties. Considering with input x and h vector represents the Impulse response of FIR filter and y represents the output y= h*x. in the matrix form the convolution can be represented as y=Hx where H is the circulant matrix which is diagnosed by the Fourier matrix F. |
 |
| Where D represents the diagonal matrix and speed up by using FFT. For fast reconstruction here we use an Circulant-IOMP algorithm. With the help of this algorithm the simple selection of certain measurements points are obtained with minimum iterations so as to obtain a reconstruction image accurately without the necessity of extra measurement points. |
(1) Initializing the values i.e., residual  index set , orthogonal projection function and decomposition coefficients iteration count t =1 . |
(2) Compute the following formulae for n= 1, 2, 3…d:   |
 |
SIMULATION RESULTS |
| For the simulation analysis considered a Frame sample with 256x256 resolution image and simulate using Matlab. Use circulant matrix as a measurement matrix with Measurement time as M where M=cKlog(N/K) for reconstructing image. Fig.1 shows the original image, fig 2. illustrates the interpolated image using sparse based I-OMP coding and Fig.3 is the interpolated image using circulant matrix integrated with the circulant-IOMP algorithm. |
 |
 |
| Table I. The relation between the measurement times, MSE, PSNR and Reconstruction time using integration of circulant matrix and circulant-IOMP algorithm. |
 |
the quality of the interpolated image can be justified by using the original and interpolated image. For calculating the error analysis in the reconstructive image to measure the quality of the interpolated image we use relative error which is defined as for measuring the quality of the reconstruction image under different measurement times and matrices. The Fig.4 illustrates the comparison of the comparison of reconstruction errors between Circulant matrix, sparse projection matrix and the Gaussian matrix. The results show that the Circulant matrix with few measurement points can reconstruct image efficiently in comparison to other matrices. By increasing the measurement time the relative reconstruct error is less or near to the 0 value which shows the CS asymptotic characteristics in circulant in comparison to the sparse projection and Gaussian matrix |
 |
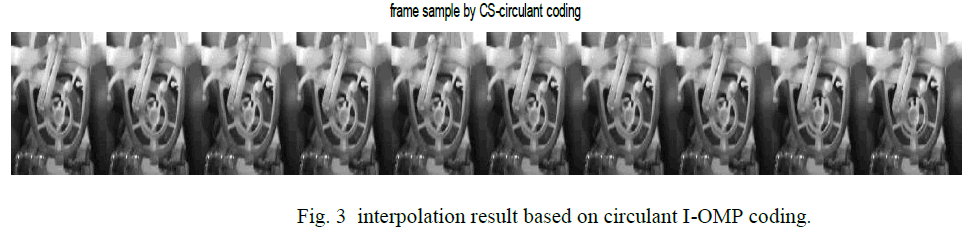
| Fig. 4. the comparison of reconstruction errors between proposed circulant matrix, Gaussian matrix and sparse projection matrix |
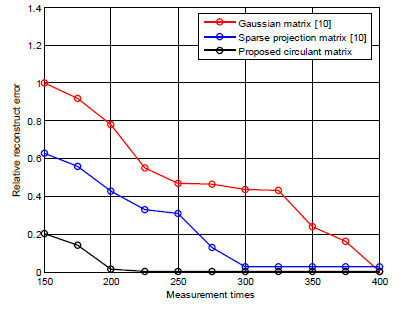
| From the Fig.5 one can see that the reconstruction error is more in IOMP algorithm in comparison with the proposed circulant-IOMP algorithm. The simulation results show that reconstruction image can be obtained with less reconstruct errors with same measurement times. In comparison with (IOMP) algorithm, the proposed circulant-IOMP algorithm requires less non adaptive measurements. |
 |
| Fig. 5. The comparison of reconstruction errors between IOMP algorithm and the proposed circulant-IOMP algorithm |
| Fig.6 illustrates the measurement time vs. the reconstruct using IOMP algorithm and proposed circulant-IOMP algorithm. The below fig.4 shows that to reconstruct image by using the same measurement time the proposed circulant-IOMP takes less time to reconstruct image in comparison with the conventional IOMP algorithm. By this one can say that the projection and the reconstruction image is much faster in proposed circular-IOMP |
 |
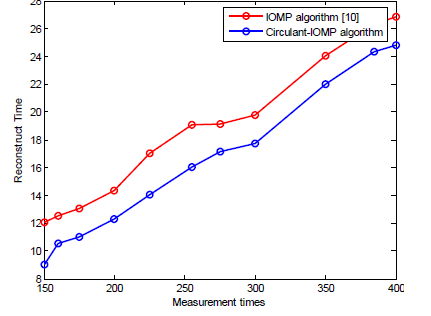| Fig. 6. measurement times vs. reconstruction time using circulant IOMP and IOMP algorithm |
CONCLUSION |
| In this paper we have applied the compressed sensing theory which enhance the signal acquisition greatly and has a broad research prospect in different fields. By using the compressive sensing we have evaluated the measurements in order to rebuild high resolution image by proposing a circulant measurement matrix and a circulant-IOMP algorithm. The simulation results shows that, a high resolution images can be interpolated accurately with few measurement points by integrating the circulant measurement matrix along with circulant-IOMP algorithm. In comparison to the conventional IOMP algorithm |
References |
|