International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Reversible Multiplier – A Review

Mandeep Kaur1, Harpreet Singh1, Chakshu Goel3
  1. PG student, Dept. of ECE, ShaheedBhagat Singh State Technical Campus, Ferozepur, Punjab, India
  2. Assistant Professor, Dept. of ECE, ShaheedBhagat Singh State Technical Campus, Ferozepur, Punjab, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Increasing demand for reduction in power dissipation in digital computer system has led to new mode of computation for digital design giving birth to reversible computing. Its main aim is low power dissipation in logical elements but can have some other advantages likeerror preventionand data security. In present-day, reversible logic has bring out to be an optimistic computing model having applications in low power CMOS, nanotechnology, quantum computing and DNA computing. This paper presents reviews about various purposed schemes used to designn×nreversible multiplier. The reversible multipliers are optimized in terms of total quantum cost, number of ancillary inputs, number of garbageoutputs and hardware complexity.

Keywords
Reversible logic gate, Reversible logic circuit, Reversible multiplier, Quantum computing, Nanotechnology.

INTRODUCTION
The usual general- purpose computing system is logically irreversible unavoidably generate heat. The inputs are not generalized from the outputs in irreversible logic.During any computation the intermediate bits used to compute the final results are erased. Hence, information loss causes energy dissipation in computing system was demonstrated by R.Landauer in the year 1960. According to Landauer’s[1] principle, a computer must dissipate atleast kTIn2 of energy (about 3×10-21 J at room temperature) for each bit of information is erased, where k = 1.3806505×10-23 is Boltzman constant and T =273.16 K is absolute temperature. Gordon. E. Moore [2] in 1965 predicted that the number of transistors onto a chip will double after every 18 months. According to Moore’s law as the number of components on the chip increases the power dissipation also increases rapidly. Hence power dissipation has become an important issue in integrated circuits.In 1973, C.Bennett [3] ,revealed that the reversible logic circuits would not loose kTIn2 joules of energy as outputs can be recovered from inputs.Bennett showed that the computations that are performed on classical machine can be performed with the same efficiency with less power dissipation on the reversible machine. The research on the reversibility was started in 1980’s based on Bennett’s concept.Shor[4]in 1994 did a remarkable research work in creating an algorithm using reversibility for factorizing large numbers with better efficiency than the classical computing theory. After his work on reversible computing has been started in different fields such as quantum computing, low power CMOS design and nanotechnology.

RELATED WORK
Because of extensive use of multipliers in computer system, several reversible circuits for implementing multipliers have been purposed. Reversible multiplier is a computingdevice, used to multiply two binary numbers by the use of reversible adders. The basic multiplication process involves computing a set of partial products, and then summing the partial products together.
In 2008, Haghparast et al.[5] have introduced a reversible multiplier structure.The design uses an array of 16 Peres gates for the generation of partial products and then addition of partial products is accomplished by adder designed with combination of Peres gate and HNG gate. In the same year, Shams et al.[6] purposed the similar design with the Peres gates for the partial product generation and MKG for the addition at final stage of multiplication.
In year 2010, a new design for reversible 4×4 multiplier is purposed by H.R. Bhagyalakshmi et al.[7]It consists of three sections for multiplication; additional is fan-out circuit along with partial product generator and additional circuits. In year 2012, M..Z. Moghadamet al.[8] purposed two approaches to design the ultra- area- efficient multiplier, in which partial product generation is carried out with Peres and Toffoli gates respectively. The number of garbage outputs are reduced when partial products are generated with Peres gate and Toffoli gate.

REVERSIBLE GATES
A reversible logic gate is an n-input, n-output device with one-to-one mapping[3], which helps to retrieve the inputs from the outputs and vice-versa. The main challenges for the reversible logic are reducing the power dissipation, reducing number of gates, delay and quantum cost.

1.The Reversible logic:
The n-input and k-output Boolean function f(a1,a2,a3…an) is called reversible function if :
i. Mapping is one-to-one between input vector and output vector.
ii. The number of inputs is equal to number of outputs.
iii. Fan-out and feedback are not permitted.

2.Basic Definitions Related To Reversible Logic:
(i)Quantum Cost: The Quantum Cost refers to the cost of the circuit in terms of the cost of primitive gates (number of gates composed the circuit). The quantum cost of NOT gate (1×1) is 0 and that of any 2×2 gate (CNOT or Feynman gate) is 1.[11]
(ii) Constant Inputs / Ancillary Inputs:Ancillary/constant inputs can be defined as the inputs to be retained at constant value of ‘0’ or ‘1’ in order to generate the given logical function.[9]
(iii)Garbage Outputs:The garbage outputs are additional outputs in the reversible logic circuit that maintain the reversibility logic but do not perform any useful operation [10].The following formula shows relation between Garbage Output and Ancillary Inputs:
Input (n) + Constant/Ancillary Input = Output (k) + Garbage Output.
(iv)Total Logical calculations:The total logical calculation [10] is another term in reversible logical circuits, which indicates the XORs, NOTs and ANDs .Total Logical calculations are represents by the (L).Hereα =number of XORs,β =number of ANDs andδ =number of NOT gates.

3.Basic Reversible Logic Gates:
An n-input and n-output function fn is said to be reversible if and only if there is a one-to-one [2]correspondence between the inputs and the outputs. An N×N reversible logic gate can be represents as follow:
image
Where Ivector and Ovector are input and output vectors respectively.In reversible logic gates, number of inputs(n) are equal to number of outputs(n).In this section we review the Reversible logic gates.
(i)Feynman Gate:Feynman gate is 2×2 reversible gates[11], called as CNOT (Controlled NOT) gate. It is widely used as fan-out purposes.Quantum cost for Feynman gate is 2.The total logical calculations of this gate is; T= 1α.
image
The input and outputvectors of 2×2 Feynman gate are as follows:
image
(ii)Toffoli Gate:ToffoliGate is also called as CCNOT (Controlled Controlled NOT) gate is a 3×3 reversible gate[12]. TG is a universal reversible gate.If the target input (C) is set to ‘0’,then the gate will perform AND operation. Quantum Cost for Toffoli gate is 5. The total logical calculations of this gate are; T= 1α+1β.
image
The input and output vectors of 3× 3 Toffoli gate is:
image
(iii)Peres Gate:Peres gate is a new 3×3 Toffoligate[13]. Quantum Cost for Peres gate is 4. Due to less quantum cost, it is used to implement several logic functions. Peres gate can be used as half adder, and a two-input AND gate. The total logical calculations for Peres gate are (T)= 2 α+1β.
image
The input and output vector of 3× 3 Peres gate:
image
(iv)HNG Gate:HNG is 4×4 reversible gates. HNG can singly work as reversible full adder [5]. Thus QC of HNG full adder is minimum possible QC for a full adder design. (QC= 6). The total logical calculations for TSG gate is 5α + 2β.
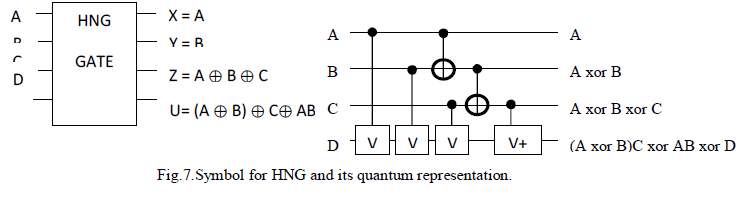image
The inputs and outputs vectors of HNG gate are as follows:
image
image
(v)TSG Gate:TSG is a 4×4 reversible gate. The TSG gate is capable of implementing all Boolean functions and can also work as reversible full adder[15]. The total logical calculations for TSG gate are 6α + 3β + 3δ.
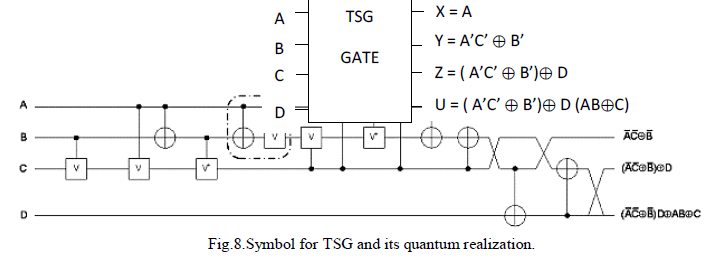image
The inputs and outputs vector of TSG gate are as follows:
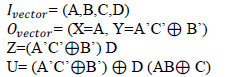image
(vi)MKG Gate:MKG is 4×4 reversible logic. It can also singly work as a reversible full adder.[5]. Qunatum cost for MKG gate is 13. The total logical calculations for MKG gate are 5α + 3β + 3δ.
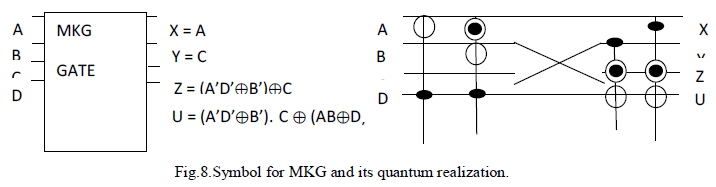image
The inputs and outputs vectors of MKG gate are as follows:
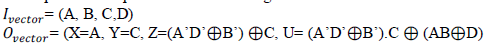image

QUANTUM COMPUTING THEORY
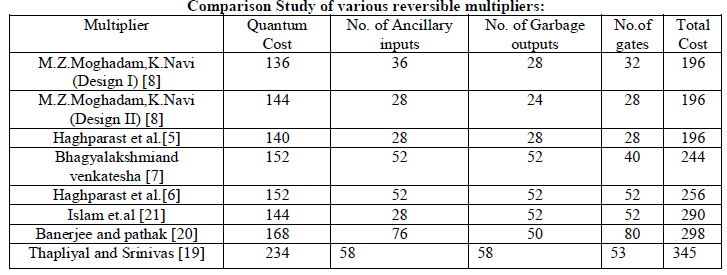image
image
image
In 2006,Thapliyal and Srinivas [19] proposed a reversible multiplier, using TSG gates. Total quantum cost for multiplier was 345. Many researchers then after proposed multiplier using different reversible gates.Quantum cost further reduced to 244 by a new improved design purposed by H.R. Bhagyalakshmi [5] in 2010. In year 2012, a design is purposed by M.Z.Moghadam et al. This design reduces the quantum cost to 196 by the use of TG [12] and PG[13] gates for the partial product generation.

APPLICATIONS
Reversible computing is used in areas which require high energy efficiency, speed and performance. It includes the areas like:
• Design of low power arithmetic and data path for digital signal processing (DSP) .
• Low power CMOS design.
• DNA Computing
• Quantum Computer
• Computer Graphics
• Nanotechnology
• FPGA in CMOS Design

CONCLUSION
Reversible multiplier can be designed with the different logical designs purposed in conventional combinational and sequential logic with the aim to improve the performance of computational units. To improve the performance, the main measures in designing an efficient reversible logic multiplier are: Number of gates, Number of garbage outputs, Number of ancillary inputs, total quantum cost and total logical calculations.

References
  1. R.Landauer, “Irreversiblity and Heat Generation in the Computational Process”, IBMJournal of Research and Development,5,pp.183-191,1961.
  2. Gordon. E. Moore,“ Cramming more components onto integated circuits Electronics”, J. Electron., Volume 38, Number 8, April 19,1965.
  3. Bennett C. H., “ Logical reversibility of Computation”,IBM J. Research and Development,pp.525-532,1973.
  4. PetrerShor, “Algorithms for quantum computation: discrete log and factoring”, Proc.35th Annual Symp. On Found. Of Computer Science, IEEE ComputerSociety, Los Alamitos, pp. 124-134, 1994.
  5. M. Haghparast, S. Jafaralijassbi, Keivan.Navi, O.Hashemipour, “Design of a novel Reversible multiplier circuit using HNG gates in Nanotechnology”, World Appl. Sci.J, Volume 3, Journal 6 ,pp. 974-978,2008
  6. M.Shams, K.Navi, M. Haghparast., “Novel reversible multiplier circuit in Nanotechnology”. doi:10.1016/j.mejo.2011.05.007
  7. H.R. Bhagyalakshmi, M.K. Venkatesha, “An improved design of a multiplier using Reversible logic gates”, Int.J.Engg.Sci.Tech, Volume 2, Number 8,pp. 3838-3845, 2010.
  8. M.Z.Moghadam, K.navi.,“Ultra- area- efficient reversible multiplier”, Microelectronic .J. pp.377-385, 2012.
  9. Dmitri Maslov, Gerhard W. Dueck,“Reversible cascades with minimal garbage”, IEEE Transactions on CAD of Integrated Circuits andSystems Volume 23, Number 11,,pp.1497-1509,2004.
  10. E.P. Ali Akbar, M. Haghparast and K.Navi, “ Novel design of fast reversible Wallace Sign multiplier circuit in nanotechnology”, Microelectronic.J. Volume 42,pp.973-981,2011.
  11. Feynman, R, 1985. “Quantum mechanical computers”, Optics News, 11:11-20.
  12. T.Toffoli,,“Reversible Computing”, Tech memo MIT/LCS/TM-151, MIT Lab for Computer Science ,1980.
  13. [13] A.Peres, “Reversible Logic and Quantum Computers”, Physical Review A, Gen. Phys.,vol. 32, pp.3266-3276,Dec 1985.
  14. E.Fredkin, T Toffoli, “Conservative Logic” , International Journal of Theor. Physics, Volume 21 ,pp.219-253,1982.
  15. Thapliyal H., and M.B. Srimivas, 2005. “Novel reversible TSG gate and its applications for designing reversible carry look ahead adder and other adder architectures”, roceedings of the 10th Asia-Pacific Computer Systems Architecture Conference (ACSAC) LectureNotes of Computer Science, Springer- verlag, 3740: 775-786.
  16. P.Kaye, Raymond Laflamme, Michele Mosa, “An introduction to Quantum Computing”,Oxford university Press e-Book- Ling,ISBN 0-19-857000- 7,Jan 2007.
  17. A. Barenco, C.H. Beneet, R. Cleve, D.P. Divincenzo, N. Margolus, P.Shor, T. Sleator, J.A. Smolin, H. weinfuriter, “Elementary gates for quantum computing”, Phys. Rev. A52 (5) ,pp. 3457-3467,1995.
  18. William N.N. Hung , X. Song et al.,“Optimal synthesis of multiple output Boolean functions using a set of quantum gates by symbolic reachability analysis”, IEEE transaction on computer-aided design of integrated circuit and systems, vol.25, No. 9,Sep.2006.
  19. H.Thapliyal, M.B.Srinivas, “Novel reversible multiplier architecture using Reversible TSG gate”, in :Proceedings of IEEE international Conference on Computer System and Applications,pp.100-103, 2006.
  20. Benerjee and A. Pathak , “An analysis of reversible multiplier circuits”.<arXiv:0907.3357>,pp.1-10, 2009.
  21. M.S. Islam,et al., “ Low Cost Quantum realization of reversible multiplier circuits”, Inf.Technol.J.,Volume 8,pp. 208, 2009.