ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Debirupa Hore1, Dutta Chowdhury2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This Paper presents a review on the discussion of different types of population based Artificial intelligence optimization techniques used in the distributed generations in Distributed Networks. With the growing popularity of the Distributed Generations in the recent world it is required to determine the optimal location and size of the Distributed generations along with the reduction of the loss, improvement of Voltage Profile and reliability at lowest cost. For this different types of optimization techniques are used such as Firefly Algorithm, Genetic Algorithm, BFO, PSO, Artificial Bee Colony, Clonal Selection Algorithm, Ant Colony Optimization etc. This population based optimization techniques are more flexible and fast optimization methods.
Keywords |
| Distributed Generations Firefly Algorithm, Genetic Algorithm, BFO, PSO, Artificial Bee Colony, Clonal Selection Algorithm, Ant Colony Optimization. |
INTRODUCTION |
| Increasing the demand for electrical energy, tight restriction on expanding distribution lines to supply remote areas and system reliability are three main issues which have increased the desirability of DGs in recent years. Although, use of DGs can lead the distribution network to lower loss, higher reliability, etc, it can also apply a high capital cost to the system. This demonstrates the importance of finding the optimal size and placement of DGs. Although minimizing the power loss and improving the reliability simultaneously will yield a better solution than optimizing individually. Because of the considerable advantages of DG-unit application (e.g., power loss reduction, environmental friendliness, voltage improvement, postponement of system upgrading, and increasing reliability), there has been a significant rise in interest by researchers. Practical application of the DG-unit, however, proves difficult. Social, economic, and political factors affect the final optimal attained solution. Solution techniques for DG-unit deployment are attained via different optimization methods. Optimization tools have been employed to solve different DG-unit problems. Tools such as genetic algorithm (GA), evolutionary programming (EP), and particle swarm optimization (PSO) are promising and still evolving in this field. Some of those techniques have been modified to enhance their solution performance or to overcome other limitations. In addition, most of these tools have many parameters to be tuned. |
PROBLEM FORMULATION |
| The problem investigated in this research is to find the optimal DG power rating and bus location simultaneously that make the radial distribution network real losses a minimum. |
| The real power losses are given as: |
| N is the total number of branches in the system, |
| Ri is the branch resistance. |
| Based on equation 1, the line power losses could be reduced by lowering the branch currents in the distribution network. One way to reduce the current in certain parts of the network is to introduce the DG. |
| The problem is formulated as one of constrained mixed integer nonlinear programming with the location being discrete and the size being continuous. In the developed algorithm, the objective function to be minimized is the total network power losses while satisfying certain constraints imposed on the system variables. The objective function is as follows:- |
| Minimize PLoss |
| The equality constrains are the non-linear power flow equations of the radial distribution system. They can be written in vector form as follows:- |
| Where, x is the state vector which represents the dependent variables. |
| U is the control vector that represents the independent variables. |
| The inequality constraints are the voltage limits imposed on the radial distribution system as follows:- |
| Where, j is the distribution bus number. |
| The inequality constraint associated with the DG real power output is as follows:- |
GENETIC ALGORITHM (GA) |
| The Genetic Algorithm (GA) is a method for solving both constrained and unconstrained optimization problems that are based on natural selection, the process that drives biological evolution. The GA repeatedly modifies a population of individual solutions. At each step, the GA selects individuals at random from the current population to be parents and uses them to produce the children for the next generation. Over successive generations, the population "evolves" toward an optimal solution The GA uses two main types of rules at each step to create the next generation from the current population: |
| 1) Selection rules select the individuals, called parents that contribute to the population at the next generation. |
| 2) Reproduction is the step used to generate a second generation population of solutions from those selected through genetic operators: crossover (also called recombination), and/or mutation: a- Crossover rules combine two parents to form children for the next generation, b- Mutation rules apply random changes to individual parents to form children. For detailed description of GA refer to reference |
ARTIFICIAL BEE COLONY ALGORITHM |
| The artificial bee colony (ABC) algorithm is a new meta heuristic optimization approach, introduced in 2005 by Karaboga [13]. Initially, it was proposed for unconstrained optimization problems. Then, an extended version of the ABC algorithm was offered to handle constrained optimization problems [15]. Furthermore, the performance of the ABC algorithm was compared with those of some other well-known population-based optimization algorithms, and the results and the quality of the solutions outperformed or matched those obtained using other methods [15]–[19]. The colony of artificial bees consists of three groups of bees: employed, onlookers, and scout bees. The employed bees are those which randomly search for food-source positions (solutions.) Then, by dancing, they share the information of that food source, that is., nectar amounts (solutions’ qualities), with the bees waiting in the dance area of the hive. Onlookers are those bees waiting in the hive’s dance area. The duration of a dance is proportional to the nectar content (fitness value) of the food source currently being exploited by the employed bee. Hence, onlooker bees watch various dances before choosing a food source position according to the probability proportional to the quality of that food source. Consequently, a good food-source position (solution) attracts more bees than a bad one. Onlookers and scout bees, once they discover a new food-source position (solution), may change their status to become employed bees. Furthermore, when the food-source position (solution) has been visited (tested) fully, the employed bee associated with it abandons it, and may once more become a scout or onlooker bee. In a robust search process, exploration and exploitation processes must be carried out simultaneously. In the ABC algorithm, onlookers and employed bees perform the exploration process in the search space, while on the other hand, scouts control the exploration process. Inspired by the aforementioned intelligent foraging behavior of the honey bee [13], the ABC algorithm was introduced. One half of the colony size of the ABC algorithm represents the number of employed bees, and the second half stands for the number of onlooker bees. For every food-source’s position, only one employed bee is assigned. In other words, the number of food-source positions (possible solutions) surrounding the hive is equal to the number of employed bees. The scout initiates its search cycle once the employed bee has exhausted its food-source position (solution.) The number of trials for the food source to be called “exhausted” is controlled by the limit value of the ABC algorithm’s parameter. Each cycle of the ABC algorithm comprises three steps: first, sending the employed bee to the possible food-source positions (solutions and measuring their nectar amounts (fitness values); second, onlookers selecting a food source after sharing the information from the employed bees in the previous step; third, determining the scout bees and then sending them into entirely new food-source positions. |
| The ABC algorithm creates a randomly distributed initial population of solutions (i=1, 2,…..Eb), where, i signifies the size of population and Eb is the number of employed bees. Each solution Xi is a D-dimensional vector, where D is the number of parameters to be optimized. The position of a food-source, in the ABC algorithm, represents a possible solution to the optimization problem, and the nectar amount of a food source corresponds to the quality (fitness value) of the associated solution. After initialization, the population of the positions (solutions) is subjected to repeat cycles of the search processes for the employed, onlooker, and scout bees( cycle=1,2,……MCN), where MCN is the maximum cycle number of the search process. Then, an employed bee modifies the position (solution) in her memory depending on the local information (visual information) and tests the nectar amount (fitness value) of the new position (modified solution.) If the nectar amount of the new one is higher than that of the previous one, the bee memorizes the new position and forgets the old one. Otherwise, she keeps the position of the previous one in her memory. After all employed bees have completed the search process, they share the nectar information of the food sources and their position information with the onlooker bees waiting in the dance area. An onlooker bee evaluates the nectar information taken from all employed bees and chooses a food source with a probability related to its nectar amount. The same procedure of position modification and selection criterion used by the employed bees is applied to onlooker bees. The greedy-selection process is suitable for unconstrained optimization problems. However, to overcome the greedy-selection limitation specifically in a constrained optimization problem [13], Deb’s constrained handling method [21] is adopted. It employs a tournament selection operator, where two solutions are compared at a time when the following conditions are imposed: 1) any feasible solution is preferred over an infeasible one; 2) among two feasible solutions, the one with better objective function value is preferred; and 3) among two infeasible solutions, the one having the smaller constraint violation is preferred. The probability of selecting a food-source Pi by onlooker bees is calculated as follows: |
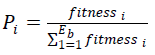 |
| Where is the fitness value of a solution i and , and is the total number of food-source positions (solutions) or, in other words, half of the colony size. Clearly, resulting from using (9), a good food source (solution) will attract more onlooker bees than a bad one. Subsequent to onlookers selecting their preferred food-source, they produce a neighbor foodsource position i+1 to the selected one i, and compare the nectar amount (fitness value) of that neighbor i+1 position with the old i position. The same selection criterion used by the employed bees is applied to onlooker bees as well. This sequence is repeated until all onlookers are distributed. Furthermore, if a solution does not improve for a specified number of times (limit), the employed bee associated with this solution abandons it, and she becomes a scout and searches for a new random food-source position. Once the new position is determined, another ABC algorithm cycle MCN starts. The same procedures are repeated until the stopping criteria are met. |
| In order to determine a neighbouring food-source position (solution) to the old one in memory, the ABC algorithm alters one randomly chosen parameter and keeps the remaining parameters unchanged. In other words, by adding to the current chosen parameter value the product of the uniform variant [-1, 1] and the difference between the chosen parameter value and other “random” solution parameter value, the neighbor food-source position is created. The following expression verifies that: |
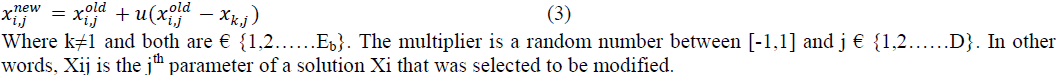 |
| When the food-source position has been abandoned, the employed bee associated with it becomes a scout. The scout produces a completely new food-source position as follows: |
| where equation applies to all j parameters and u is a random number between[-1,1]. If a parameter value produced using above two equations exceeds its predetermined limit, the parameter can be set to an acceptable value. The value of the parameter exceeding its limit is forced to the nearest (discrete) boundary limit value associated with it. Furthermore, the random multiplier number u is set to be between [0 1] instead of [-1, 1]. Thus, the ABC algorithm has the following control parameters: |
| 1. The colony size CS, that consists of employed bees Eb plus onlooker bees Eo; |
| 2. The limit value, which is the number of trials for a food-source position (solution) to be abandoned; and |
| 3. The maximum cycle number MCN. |
A. ABC ALGORITHM FOR DG-UNIT APPLICATION PROBLEM |
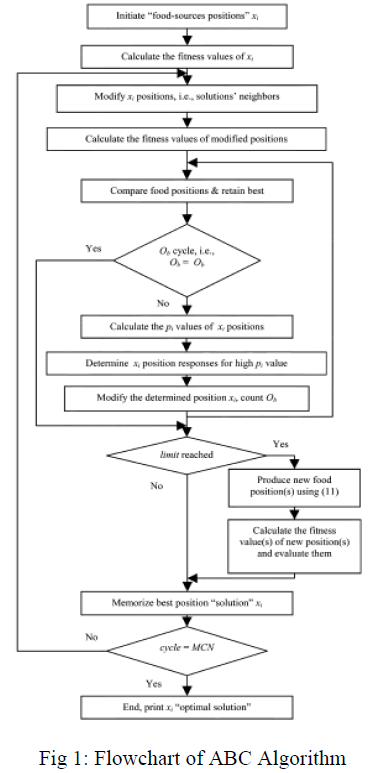
| The flowchart of the ABC algorithm is illustrated in Fig. 2. |
| The solution steps of the proposed ABC algorithm for DG-unit application are described as follows steps. |
| 1) Initialize the food-source positions xi (solutions population), where i-(1, 2……Eb. The xi solution form is as follows. |
| 2) Calculate the nectar amount of the population by means of their fitness values using fitness. |
| Where, represents the response of Objective Function at solution i. |
| 3) Produce neighbor solutions for the employed bees by using (3) and evaluate them as indicated by 2. |
| 4) Apply the selection process. |
| 5) If all onlooker bees are distributed, go to Step 9). Otherwise, go to the next step. |
| 6) Calculate the probability values pi for the solutions xi using (2). |
| 7) Produce neighbor solutions for the selected onlooker bee, depending on the value, using (3) and evaluate them as Step 2) indicates. |
| 8) Follow Step 4). |
| 9) Determine the abandoned solution for the scout bees, if it exists, and replace it with a completely new solution sing (4) and evaluate them as indicated in Step 2). |
 |
HYBRID PARTICLE SWARM OPTIMIZATION APPROACH |
| In 1995, Kennedy and Eberhart first introduced the PSO method, motivated with the social behavior of organisms such as fish schooling and bird flocking. PSO, as an optimization tool, provides a population based search procedure in which individuals called particles change their positions (states) with time. In a PSO system, particles fly around in a multidimensional search space. During flight, each particle adjusts its position according to its own experience, and the experience of neighboring particles, making use of the best position encountered by itself and its neighbors. The swarm direction of a particle is defined by the set of particles neighboring the particle and its history experience. |
| Let x and v denote a particle coordinates (position) and its corresponding flight speed (velocity) in a search space, respectively. Therefore, the ith particle is represented as xi = (xi1 + xi2 … … . xid) in the d dimensional space. The best previous position of the ith particle is recorded and represented as |
| pbesti = (pbesti1, pbesti2, … … … . . pbestid |
| The index of the best particle among all the particles in the group is represented by gbestd the rate of the velocity for particle i is represented as |
| vi = (vi1, vi2, … . , vid). |
| The modified velocity and position of each particle can be calculated using the current velocity in distance from pbestid to gbestd |
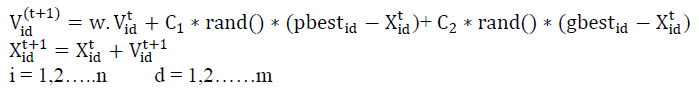 |
| Where: n is the number of particles in a group. m is the number of members in a particle. t is the pointer of iterations. w is the inertia weight factor. C1 and C2are two uniform random values in the range [0,1]. |
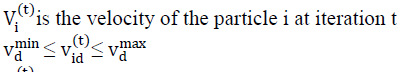 |
| Xi (t) is the current position of particle i at iteration t. in the above procedures, the parameter Vmax determines the resolution, or fitness, with which regions are to be searched between the present position and the target position. If Vmax is too high, particles might fly past good solutions. If Vmax is too small, particles may not explore sufficiently beyond local solutions. In many experiences with PSO, Vmax was often set at 10-20% of the dynamic range of the variable on each dimension. The constants C1 and C2 represent the weighing of the stochastic acceleration terms that pull each particle toward the pbest and gbest positions. Low values allow particles to roam far from the target regions before being tugged back. On the other hand, high values result in abrupt movement towards, or past, target regions. Hence the acceleration constants C1and C2 were often set to be 2.0 according to past experiences. Suitable selection of inertia weight w provides a balance between global and local explorations, thus requiring less iteration on average to find a sufficiently optimal solution. As originally developed, W often decreases linearly from about 0.9 to 0.4 during a run. |
| In general, the inertia weight w is set according to the following equation: |
| where: Wmax is the initial weight, Wmin is the final weight, iter is the current iteration number, and itermax is the maximum iteration number. |
| The PSO algorithm can be summarized in the following steps: |
| 1) Randomly initialize a swarm with feasible discrete position vectors. |
| 2) Randomly assign a suitable velocity vector to each particle. |
| 3) Record the fitness of the entire population. |
| 4) Determine the best particle performance among the group. |
| 5) Update velocity and position vectors according to (6) and (7) for each particle. |
| 6) Discrete the position vector. |
| 7) If any particle flies outside the feasible solution space, restore the particle to its best previously achieved feasible solution. |
| 8) Repeat steps 1 − 7 until maximum number of iterations is reached. |
CLONAL SELECTION ALGORITHM (CSA) |
| The Artificial Immune System (AIS) is a powerful computational intelligence method based on the biological immune system and the natural defense mechanism of human body. When an antigen such as a bacterium, a virus, etc. invades in the body, the biological immune system will select the antibodies, which can Clonal Selection Algorithms (CSA), which are most commonly applied to optimization and pattern recognition domains, are a class of algorithms inspired by the Clonal selection theory which has become a widespread accepted model for how the immune system responds to infections. CSA is an integrated part of Artificial Immune System (AIS), which explains how an immune response is mounted when a nonself antigen is recognized by the B cells. It is an evolutionary algorithm, where, during evolution, the antibodies which can recognize the antigens proliferate by cloning. The general steps involved in CSA are as follows: |
| Step 1: To create a population P of random solutions to the given problem. |
 |
 |
BACTERIAL FORAGING OPTIMIZATION ALGORITHM |
| This procedure called foraging is crucial in natural selection, since the animals with poor foraging strategies are eliminated, and successful ones tend to propagate. Hence, to survive, an animal or a group of animals must develop an optimal foraging policy. Some of the most successful foragers are bacteria like the E Coli, which employs chemical sensing organs to detect the concentration of nutritive or noxious substances in its environment. The bacteria then moves through the environment by a series of tumbles and runs, avoiding the noxious substances and getting closer to food patch areas in a process called Chemotaxis. Besides, the bacteria can secrete a chemical agent that attracts its peers, resulting in an indirect form of communication. |
| The foraging strategy is governed basically by four processes namely Chemotaxis, Swarming, Reproduction, Elimination and Dispersal |
| a. Chemotaxis :Chemotaxis process is the characteristics of movement of bacteria in search of food and consists of two processes namely swimming and tumbling. A bacterium is said to be 'swimming' if it moves in a predefined direction, and 'tumbling' if moving in an altogether different direction. Let j be the index of Chemo tactic step, k be the reproduction step and l be the elimination dispersal event. Let is the position of ith bacteria at jth chemo tactic step, kth reproduction step and lth elimination dispersal event. The position of the bacteria in the next chemo tactic step after a tumble is given by- |
| If the health of the bacteria improves after the tumble, the bacteria will continue to swim to the same direction for the specified steps or until the health degrades. |
| b. Swarming : Bacteria exhibits swarm behavior i.e. healthy bacteria try to attract other bacteria so that together they reach the desired location (solution point) more rapidly. The effect of Swarming is to make the bacteria congregate into groups and move as concentric patterns with high bacterial density. Mathematically swarming behavior can be modeled as- |
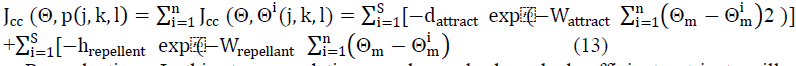 |
| c. Reproduction : In this step, population members who have had sufficient nutrients will reproduce and the least healthy bacteria will die. The healthier half of the population replaces with the other half of bacteria which gets eliminated, owing to their poorer foraging abilities. This makes the population of bacteria constant in the evolution process. |
| d. Elimination and Dispersal : In the evolution process a sudden unforeseen event may drastically alter the evolution and may cause the elimination and/or dispersion to a new environment. Elimination and dispersal helps in reducing the behavior of stagnation i.e. being trapped in a premature solution point or local optima. |
FIREFLY ALGORITHM |
| Firefly Algorithm (FA) is invented by Xin-She Yang for solving multimodal optimization problem. The development of FA is based on flashing behavior of fireflies. There are about two thousand firefly species where the flashes often unique for a particular species. The flashing light is produced by a process of bioluminescence where the exact functions of such signaling systems are still on debating. Nevertheless, two fundamental functions of such flashes are to attract mating partners (communication) and to attract potential prey. For simplicity, the following three ideal rules are introduced in FA development, 1) all fireflies are unisex so that one firefly will be attracted to other fireflies regardless of their sex, 2) attractiveness is proportional to their brightness, thus for any two flashing fireflies, the less brighter one will move towards the brighter one, 3) the brightness of a firefly is affected by the landscape of the objective function. For maximization problem, the brightness can simply be proportional to the value of the objective or fitness function. The basic steps of the FA can be summarized as the pseudo code is depicted. |
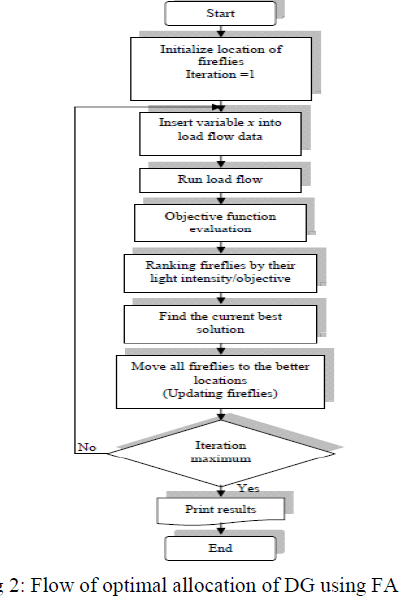 |
A. FA FOR OPTIMAL ALLOCATION OF DG |
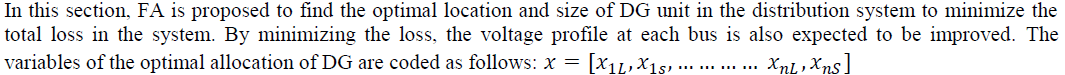 |
| Where L indicates the location of DG, S indicates the size of DG and n is the number of DG unit that need to be installed in the system. These variables then are included in the data of load flow and the load flow is executed to obtain the total loss of the system. The procedure to obtain the optimal allocation of DG requires load flow to be run iteratively. After obtaining the best location and size of DG simultaneously, the procedure is stopped. The objective function, f(x) is the results of the total loss of the system, PLoss to be minimized, as follows: |
| Where, line is number of transmission lines in the distribution system. The process of incorporating the FA into optimal allocation of DG is shown. |
ANT COLONY OPTIMIZATION (ACO) |
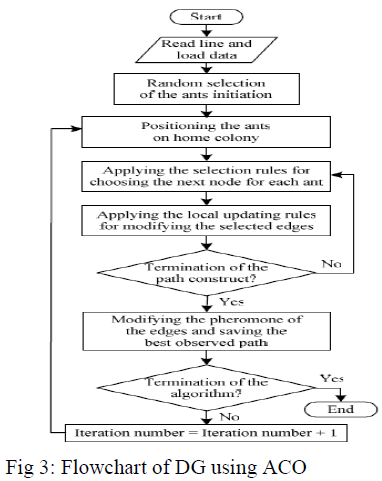
| The general ACO algorithm derived from the behavior of real ants is illustrated in The procedure of the ACO algorithm manages the scheduling of three activities. The first step consists mainly in the initialization of the pheromone trail. In the iteration (second) step, each ant constructs a complete solution to the problem according to a probabilistic state transition rule. The state transition rule depends mainly on the state of the pheromone. The third step updates quantity of pheromone; a pheromone updating rule is applied in two phases. First is an evaporation phase where a fraction of the pheromone evaporates, and then there is a reinforcement phase increasing amount of pheromone on path with high quality solutions. This process is iterated until a stopping criterion is reached. |
| Several different ways have been proposed to translate the above principles into a computational procedure to solve the optimization problem. The optimization approach proposed for in this paper is based on the ACO algorithm presented in and outlined in the next subsection. |
| Applying ACO to DG Placement Problem |
| Main steps of proposed ACO algorithm are listed below: |
| Step1) Graph representation of search space First of all, we seek to devise a representation structure that is suitable for ants to search for solutions to the problem. The searching space of the problem is shown |
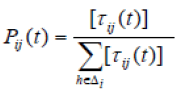 |
| All possible candidate capacity values in site n are represented by the states in the searching space in correspondence to stage n. The number of stages for each load level is equal to the number of candidate nodes of distribution system for DG placement. So, total number of stages is equal to ( nld × ncd ). A solution to the problem is produced after an ant completes its decision process for the sub-paths forming a tour. |
| Step2) ACO initialization: In the beginning of ACO algorithm, the pheromone values of edges in search space are all initialized to a constant value τ0 > 0. This initialization causes ants choose their paths randomly and therefore, search the solution space more effectively. |
| Step3) Ant dispatch: In this step, the ants are dispatched and solutions are constructed based on the level of pheromone on edges. Each ant will start its tour at the home colony and choose one of the states in the next stage to move according to following transition probability. Where, τij(t) is the total pheromone deposited on edge ij at iteration t, and Δi represents the set of available edges which ant can choose at state i. After each ant ends its tour, a new solution for DG placement is generated which must be evaluated using fitness function. |
| Step4) Fitness function following update rule in our study: In this step, the fitness of tours generated by ants is assessed based on fitness function. The fitness function of the problem is defined as the inverse of the total cost (1) plus a penalty factor to the infeasible solutions (i.e., the ones violating the constraints). To speed up the convergence properties of algorithm and at the same time, to use the information that may still be useful in rejected tours, this penalty factor is linearly increased (through iterations) from zero toward a very high value. |
| Step5) Pheromone update:The aim of the pheromone value update rule is to increase the pheromone values on solution components that have been found in high fitness solutions. Also, from a practical point of view, pheromone evaporation is needed to avoid a too rapid convergence of the algorithm toward a sub-optimal region. It implements a useful form of forgetting, favoring the exploration of new areas in the search space. We use the |
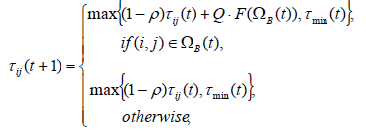 |
| where, 0 < ρ <1 is pheromone evaporation rate. ΩB(t) is the best tour found until the end of iteration t, which is stored in a specific list variable and replaced each time some ant finds a tour with better quality function value. F(ΩB(t)) is the quality function value corresponding to ΩB(t). Q is a heuristic variable which control amount of pheromone addition on the best tour. τmin(t) is lower bound of pheromone which results in a small probability for an ant to choose a certain edge; still the probability will be greater than zero. This lower bound is a function of the iteration counter as bellow: |
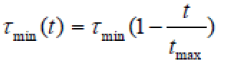 |
| where, τmin is initial lower bound of pheromone. |
| Step6) Convergence determination: The steps 3-5 continue until the iteration counter reaches the predefined maximum number which determines experimentally. The best tour selected among all iterations implies the optimal DG placement solution. Fig. 3 shows the flowchart of the proposed ACO-based solution techniques. |
 |
REVIEW OF CASE STUDY |
| Anisa Shereen[8] proposes a Genetic Algorithm (GA) based technique for the optimal allocation of Distributed Generation (DG) units in the power systems. In this paper the main aim is to decide optimal number, type, size and location of DG units for voltage profile improvement and power loss reduction in distribution network. GA fitness function is introduced including the active, reactive power losses and the cumulative voltage deviation variables with selecting weight of each variable. Two types of DGs are considered and the distribution load flow is used to calculate exact loss. Load flow algorithm is combined appropriately with GA till access to acceptable results of this operation. The effectiveness of the proposed methodology was tested on Standard IEEE33 bus system and found maximum loss reduction for each of two types of optimally placed multi-DGs. In this paper a Genetic Algorithm for optimal placement of multi-DG is proposed which efficiently minimizes the total real power loss, satisfying transmission line limits and constraints. The proposed methodology is so fast and efficient and at the same time so accurate in determining the size, type, number and location of DG unit(s). |
| Ziari, G. Ledwich et al [2] proposes that the placement and sizing of DGs are optimized using a combination of Discrete Particle Swarm Optimization (DPSO) and Genetic Algorithm (GA). This increases the diversity of the optimizing variables in DPSO not to be trapped in a local minimum. The objective of this paper is to minimize the loss and to improve the reliability at lowest cost. The constraints are the bus voltage, feeder current and the reactive power flowing back to the source side. |
| Hossam et al [7] addresses the optimization problem of integration of Distributed Generation (DG) in distribution networks. Three Genetic Algorithms (GAs) have been developed to minimize the power losses of the system. The First GAenables the optimal sizing of the DG units given their locations. Alternatively, the second GA determines the optimal locations of the DG units assuming equal sizes of the units. The third GA enables the determination of both optimal sizes, on discrete values, and optimal locations. The results prove the effectiveness of the developed genetic algorithms in finding the optimal penetration level and optimal locations and sizes of the DG units to yield minimum losses of the system. |
| AlHajari et al [1] presents a novel particle swarm optimization based approach to optimally incorporate a distribution generator into a distribution system. The proposed algorithm combines particle swarm optimization with load flow algorithm to solve the problem in a single step, i.e. finding the best combination of location and size simultaneously. In the developed algorithm, the objective function to be minimized is the total network power losses while satisfying the voltage constraints imposed on the system. It is formulated as constrained mixed integer nonlinear programming problem with the location being discrete. The 69−bus radial distribution system has been used to validate the proposed method. |
| Sulaiman, et al presents an application of Firefly Algorithm (FA) in determining the optimal location and size of Distributed Generation (DG) in distribution power networks. FA is a meta-heuristic algorithm which is inspired by the flashing behavior of fireflies. The primary purpose of firefly’s flash is to act as a signal system to attract other fireflies. In this paper, IEEE 69-bus distribution test system is used to show the effectiveness of the FA. Comparison with other method is also given. The comparison with GA also has been conducted to see the performance of FA where it is as good as GA in solving the optimal allocation problem. |
| Vahid Rashtch et al [11] proposes an approach based on Bacterial Foraging Algorithm (BFA) for optimal placement of Distribution Generations (DGs). The optimal sitting and sizing of distributed generation is formulated as a multi-objective function including the network power losses minimization and voltage profile improvement. BFA algorithm has been employed to optimize the problem. To demonstrate the effectiveness of the proposed approach, it has been applied to 33 and 69 bus systems. The results of the proposed approach are compared with those of Genetic Algorithm (GA) and also Shuffled Frog Leaping Algorithm (SFLA) to reveal its strong performance. The proposed BFA algorithm for optimal placement of DG is easy in performance without additional computational complexity. The capability of the proposed approach is tested on 33 and 69 bus systems to minimize the losses, increase the voltage stability and improve the voltage profile. The simulation results show that the BFA yields has better convergence characteristics and performance compared with the other heuristic methods such as GA and SFLA. Also the proposed technique exhibits a higher capability in finding optimum solutions by taking into account the active power and reactive power losses for objective function. |
| Fahad S.et al [3] presents a new optimization approach that employs an artificial bee colony (ABC) algorithm to determine the optimal DG-unit’s size, power factor, and location in order to minimize the total system real power loss. The ABC algorithm is a new metaheuristic, population-based optimization technique inspired by the intelligent foraging behavior of the honeybee swarm. To reveal the validity of the ABC algorithm, sample radial distribution feeder systems are examined with different test cases. Furthermore, the results obtained by the proposed ABC algorithm are compared with those attained via other methods. The outcomes verify that the ABC algorithm is efficient, robust, and capable of handling mixed integer nonlinear optimization problems. The ABC algorithm has only two parameters to be tuned. Therefore, the updating of the two parameters towards the most effective values has a higher likelihood of success than in other competing metaheuristic methods. The proposed ABC algorithm successfully achieved the optimal solutions at various test cases, as the exact and “exhaustive” ABC algorithms prove. The results of the proposed ABC algorithm were compared with those attained by other methods. Among all test cases, test case 2 had the maximum power loss reductions as well as voltage improvements. |
| Hamid Falaghi et al [4] Distributed generation (DG) placement is addressed in this paper. A cost based model to find the optimal size and location of distributed generation sources in a power distribution system is proposed in which the objective is defined as minimization of DG investment cost and total operation cost of the system. The proposed objective function and its constraints form an optimization problem which is solved using ant colony optimization (ACO) as the optimization tool. Application example is presented to demonstrate the effectiveness of the proposed methodology. A specialized ACO was employed as the solution tool of the optimization problem. The proposed DG placement algorithm has been tested in a typical distribution system. The obtained results show that the DG placement DG placement not only reduces the operating costs but also improves quality and reliability of the customers’ service. Also, it can eliminate violation of voltage and loading constraints. This effect of DG placement on distribution system is the main motivation behind DG inclusion in power distribution system planning. |
| B. Hanumantha et al [5] investigates the problem of multiple distributed generators (DG units) placement to achieve a loss reduction in radial distribution networks. Clonal selection algorithm (CSA) is proposed to determine the optimal DG-unit’s size and location is determined by loss sensitivity index (LSI) in order to maximize the net saving. Simulation studies are conducted on IEEE 33-bus and 69-bus radial test systems to verify the effectiveness of the proposed method. The efficacy and proposed of the proposed CSA is compared with existing ABC algorithm. The proposed CSA algorithm successfully achieved the optimal solutions. The results obtained by the proposed method show that the presence of DG at appropriate locations reduces energy loss costs significantly and increases savings, while the constraints of voltage profile is satisfied. The number of DG units with appropriate sizes and locations can reduce the losses to a considerable amount. The computational time was found to be dependent on the system size and number of locations. The performance of the proposed Clonal selection algorithm (CSA) shows its superiority and the potential for solving complex power system problems in terms of computational time compared to ABC solution. |
CONCLUSION |
| In this Paper a comparative Analysis was made on the optimization technique used for optimal distributed generation Allocation and sizing in Distributed Systems using different Population based artificial intelligence techniques. After case study it can be concluded that different methods used for this optimization techniques are GA, PSO, BFO, Firefly Algorithm, Artificial Bee Colony, Clonal Selection Algorithm, Ant Colony Optimization etc. he study of the papers reveals that Firefly Algorithm proves better solution in Comparison to GA, Artificial Bee Colony Algorithm proves to be more efficient method than other Methods such as GA, PSO, BFO etc. But with the development of the technology the Clonal Selection Method shows its superiority and the potential for solving complex power system problems in terms of computational time compared to ABC solution. |
References |
|