Research and Reviews - International Journals

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Menu

ISSN ONLINE(2278-8875) PRINT (2320-3765)

All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

REVIEW OF DESIGNING FOR FRACTIONALORDER FRACTIONAL-DELAY DIGITAL FILTER

Jyoti Rathi1, Rajiv Dahiya2
  1. M-Tech Scholar, Dept of ECE, PDM College of Engineering, Bahadurgarh, India
  2. Assistant Professor, Dept of ECE, PDM College of Engineering, Bahadurgarh, India
Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Design and applications of fractional order digital differentiators is the main objective of this paper. Fractional order differentiators are examples of fractional order systems. In this paper, a brief survey of the design techniques of fractional delay digital differentiator is given. Fractional delay filter is a device for band limited interpolation between samples. It finds applications in numerous fields of signal processing, including communications, array processing, speech processing, and music technology. In this paper, we present a review of FIR and all pass filter design techniques for band limited approximation of a fractional digital delay. Emphasis is on simple and efficient methods that are well suited for fast coefficient update or continuous control of the delay value. Various new approaches are proposed and several examples are provided to illustrate the performance of the methods. We focus on four applications where fractional delay filers are needed: synchronization of digital modems, in commensurate sampling rate conversion, high-resolution pitch prediction, and sound synthesis of musical instruments.

Keywords
Fractional Order, Fractional Delay

INTRODUCTION
One fundamental advantage of digital signal processing techniques over traditional analog methods is the easy implementation of a constant delay: the signal samples are simply stored in a buffer memory for the given time. This technique works perfectly as long as the desired delay is a multiple of the used sample interval. However, when a delay of a fraction of the sample interval is needed or, particularly, if it is desired to control the delay value continuously, more sophisticated methods must be used. The problem of implementing a fractional delay (FD) by digital means occurs in several applications. In one of the first treatments on the subject [1], a digital phase shifter was proposed for three problems: echo cancellation, phased-array antenna processing, and pitch-synchronous synthesis of speech.
For continuous time case, some methods for obtaining an approximated rational function using evaluation, interpolation and curve fitting techniques have been studied. These methods include Carlson’s method, Roy’s method, Chareff’s method and Oustaloup’s method [2]–[5]. For discrete time case, there have been several methods presented to design FIR and IIR filters for implementing the operator, including fractional differencing formula, Tustin method, Taylor series expansion method, continued fraction expansion, least-squares method and generalized mean method [6]–[12].
This paper is organized as follows: In section II definition of fractional delay filter is explained. And response of ideal fractional delay filter is explained. In Section III, a detail literature review of fractional delay and fractional order is described. Finally the conclusion is made.

FRACTIONAL DELAY FILTER
A fractional delay filter is a filter of digital type having as main function to delay the processed input signal a fractional of the sampling period time. There are several applications where such signal delay value is required, examples of such systems are: timing adjustment in all-digital receivers (symbol synchronization), conversion between arbitrary sampling frequencies, echo cancellation, speech coding and synthesis, musical instruments modeling etc. In order to achieve the fractional delay filter function, two main frequency-domain specifications must be met by the filter. The filter magnitude frequency response must have an all-pass behaviour in a wide frequency range, as well as its phase frequency response must be linear with a fixed fractional slope through the bandwidth. Several FIR design methods have been reported during the last two decades.
There are two main design approaches: In first one, the fractional delay filter coefficients are easily obtained through classical mathematical interpolation formulas, but there is a small flexibility to meet frequency domain specifications. On the other hand, the frequency-domain methods are based on frequency optimization process, and a more frequency specification control is available. One important result of frequency-domain methods is a highly efficient implementation structure called Farrow structure, which allows online fractional value update.
A. Ideal Fractional Delay
The delayed version of a discrete-time signal x (n) may be represented as
y (n)=x(n-D) (1)
where D is a positive integer that denotes the amount by which the signal is delayed. D can be split into the integer and fractional part as
D=int(D) + d (2)
However, Eq. 1 is meaningful only for integer values of D. In that case, the output sample is one of the previous signal samples, but for non integer values of D, the output value would lie somewhere between two samples, which is impossible (Fig. 1). Instead, the appropriate values on the sampling grid must be found via band limited interpolation. The problem can be solved by viewing a delay as a resampling process.
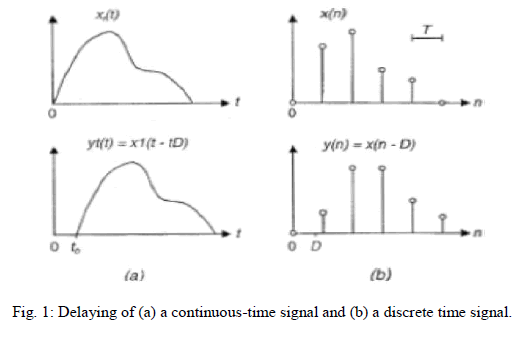image
The desired solution can be obtained by first reconstructing the continuous band limited signal and then resampling it after shifting. The task is thus related to interpolation in multirate filter design techniques or sampling rate conversion in general. Note, however that our basic constraint is to keep the sampling rate unchanged. In earlier digital signal processing theory, D can only take integer values. In other words, if the desired continuous-time delay is τ and the sampling period is T, the value of D may be obtained by rounding off the result of τ/T to the nearest integer. In many signal processing applications it is desirable that the delay D accurately represent the fractional delay, rather than the integer delay. If the Z-transform of Eq. 1 is taken, the transfer function of an ideal delay element may be written as
image
In the frequency domain, the ideal fractional-delay filter can be described as
image
The magnitude response for an ideal delay element is unity for all frequencies, while the phase response is linear with a slope of -D. This can be called an all pass system with linear phase response.
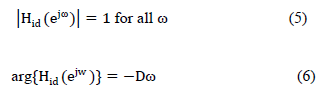image
Assuming that the discrete-time signal represents a band limited baseband signal, the implementation of a constant delay can be considered as an approximation of the ideal discrete-time linear-phase all pass filter with unity magnitude and constant group delay of the given value D. The corresponding impulse response is obtained via the inverse discrete-time Fourier transform
image
Substitution of Eq. 1.4 into Eq. 1.7 yields the solution for the ideal impulse response as
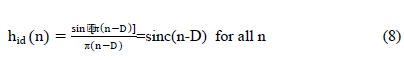image
When the desired delay D assumes an integer value, the impulse response Eq. 8 reduces to a single impulse at n = D, but for non integer values of D the impulse response is an infinitely long, shifted and sampled version of the sinc function.
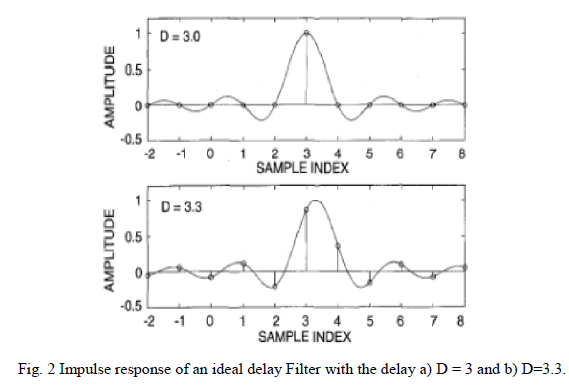image

LITERATURE REVIEW
In [13], explains the design of sinusoid-based variable fractional delay FIR filter is presented. First, the coefficients of filters are expressed as the linear combination of sinusoidal basis by using the Fourier series expansion. Then, by minimizing the weighted squares errors of frequency response, the optimal linear combination coefficients are obtained by solving a set of linear simultaneous equations. Finally, the design examples are used to demonstrate that the design error of proposed sinusoid- based method is smaller than the one of conventional polynomial-based method for the same truncation order.
In [14], explains Lagrange-type variable fractional-delay (VFD) digital alters can be directly implemented as the wellknown Farrow structure, but the fixed coefficient filters (sub filters) do not have symmetric or anti-symmetric coefficients. This paper presents a transformation matrix for transforming a causal odd-order Lagrange-type VFD filter into a new one whose all the sub filters have either symmetric or anti symmetric coefficients. As a result, the number of multipliers can be reduced by almost 50%, which not only speeds up the VFD filtering process, but also saves the cost for storing the independent sub filter coefficients.
In [15], explains a new design method for fractional delay filters based on truncating the impulse response of the Lagrange interpolation filter is presented. The truncated Lagrange fractional delay filter introduces a wider approximation bandwidth than the Lagrange filter. However, because of truncation, a ripple caused by the Gibbs phenomenon appears in the filter's frequency response. Proper choices of filter order and prototype filter order allow adjusting the overshoot to a desired level and simultaneously reducing the overall frequency-response error. The design of the proposed filter is computationally efficient, because it is based on polynomial formulas, which have common terms for all coefficients.
In [16], explains a new approach to the design of fractional delay discrete-time filters based on a multirate approach. We considered the case where it is necessary to generate a delay which is a ratio of very high integers. In order to obtain an efficient filter we propose a modification of the general poly phase structure for fractional delay.
In [18], explains the Taylor series expansion is used to transform the design problem of a fractional delay filter into the one of a first-order differentiator such that the conventional finite-impulse response and infinite-impulse response differentiators can be applied to design a fractional delay filter directly. The proposed structure is more efficient than the well-known Farrow structure in terms of filter coefficient storage because only one first-order differentiator needs to be designed and implemented. Moreover, one design example is demonstrated to illustrate the effectiveness of this new design approach.
In [19], explains a new variable fractional delay filter design method using a differentiator bank is presented. First, the Taylor series expansion is used to transform the specification of a variable fractional delay filter into that of a differentiator bank. This transform makes the design problem of the fractional delay filter reduce to the design of differentiators with different orders. A simple window method is proposed to design the differentiator bank. Finally, design examples are demonstrated to illustrate the effectiveness of this new design approach.
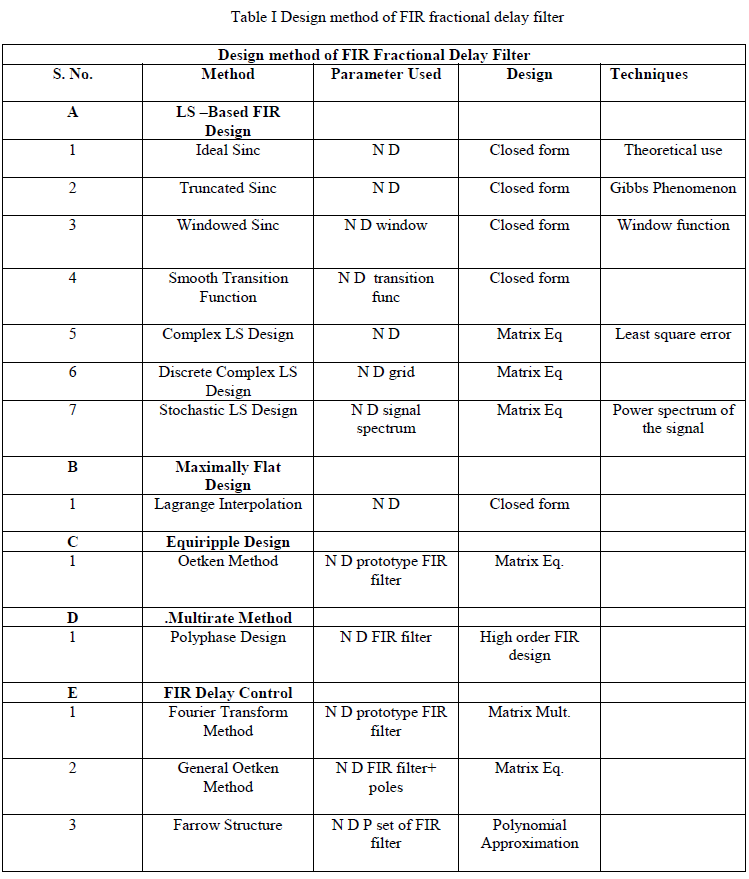
In [20], explains a digital fractional order differentiator is designed by using fractional differencing and fractional sample delay. To improve the design accuracy of the conventional fractional differencing design method at high frequency region, the integer delay is replaced by fractional sample delay. By using the well-documented FIR Lagrange and IIR allpass fractional delay filters, the proposed fractional order differentiator can be implemented easily even though the fractional sample delay is introduced. Several design examples are illustrated to demonstrate the effectiveness of the proposed method. Table. 1 shows the design method of FIR fractional delay filter.
In [22], explains the design of a digital differentiator is investigated. First, the relation between fractional sample delay filter and digital differentiator is established such that the differentiator can be obtained from the fractional delay fillter by using the computation of limit. Then, conventional finite impulse response (FIR), allpass and Farrow-based fractional delay filters are directly applied to design the digital differentiator. Finally, several design examples are illustrated to demonstrate the effectiveness of this new design approach.
In [23], explains the design of variable fractional delay filter using expansions of hyperbolic functions is presented. First, the ideal frequency response is decomposed into the sum of hyperbolic cosine and sine functions. Then, the power series expansions of hyperbolic functions are used to implement and design variable fractional delay filter. Next, the infinite product expansions of hyperbolic functions are also applied to obtain another design method of variable fractional delay filter. Finally, the numerical examples are demonstrated to show the effectiveness of the proposed design approaches.
image

CONCLUSION
In this paper, we consider the general problem of approximation of a delay that is a fractional part of the sampling interval as well as the fractional order that is the important part of fractional derivative. Both FIR fractional order and FIR fractional delay filter design techniques have been reviewed. The fractional delay approximation and fractional order calculation are generic problems which is encountered in several fields and applications of DSP.

References
  1. R. E. Crochiere, L. R. Rabiner, and R. R. Shively, A novel implementation of digital phase shifters, Bell Syst. Tech. J., vol. 54, no. 8, pp. 1497-1502, Oct. 1975.
  2. G. E. Carlson and C. A. Halijak, “Approximation of fractional capacitors by a regular Newton process,” IRE Trans. Circuit Theory, vol. 11, pp.210–213, 1964.
  3. S. C. D. Roy, “On the realization of a constant-argument immitance of fractional operator,” IRE Trans. Circuit Theory, vol. 14, pp. 264–274, 1967.
  4. A. Chareff, H. H. Sun, Y. Y. Tsao, and B. Onaral, “Fractal system as represented by singularity function,” IEEE Trans. Autom. Contr., vol.37, pp. 1465–1470, Sep. 1992.
  5. A. Oustaloup, F. Levron, B. Mathieu, and F. M. Nanot, “Frequency- band complex noninteger differentiator: Characterization and synthesis,” IEEETrans. Circuits Syst. I, Fundam. Theory Applicat.,vol. 47, pp. 25–39, Jan. 2000.
  6. C. C. Tseng, “Design of fractional order digital FIR differentiators,” IEEE Signal Process. Lett., vol. 8, pp. 77–79, Mar. 2001.
  7. Y. Q. Chen and K. L. Moore, “Discrete schemes for fractional-order differentiators and integrators,” IEEE Trans. Circuits Syst. I, Fundam. Theory Applicat., vol. 49, pp. 363–367, 2002.
  8. Y. Q. Chen and B. M. Vinagre, “A new IIR-type digital fractional order differentiator,” Signal Processing, vol. 83, pp. 2359–2365, 2003.
  9. J. A. T. Machado, A. M. Galhano, A. M. Oliveira, and J. K. Tar, “Approximating fractional derivatives through the generalized mean,” Communications in Nonlinear Science and Numerical Simulation, vol. 14, pp. 3723–3730, Nov. 2009.
  10. R. S. Barbosa, J. A. T. Machado, and M. F. Silva, “Time domain design of fractional differintegrators using least-squares,” Signal Processing, vol. 86, pp. 2567–2581, 2006.
  11. H. Zhao, G. Qiu, L. Yao, and J. Yu, “Design of fractional order digital FIR differentiators using frequency response approximation,” in Proc. 2005 Int. Conf. Communications, Circuits and Systems,May 2005, pp.1318–1321.
  12. C. C. Tseng, “Improved design of digital fractional-order differentiators using fractional sample delay,” IEEE Trans. Circuits Syst. I: Reg. Papers, vol. 53, pp. 193–203, Jan. 2006.
  13. Chien-Cheng Tseng, "Design of sinusoid-based variable fractional delay FIR filter using weighted least squares method", Circuits and Systems, ISCAS '03. Proceedings of International Symposium Volume: 3 Pag:546-549, 2003.
  14. Tian-Bo Deng, "Transformation matrix for odd-order Lagrange-type variable fractional-delay filters", Information, Communications & Signal Processing, 2007 6th International Conference, Pag:1-5, 2007.
  15. Valimaki, V.; Haghparast, A. "Fractional Delay Filter Design Based on Truncated Lagrange Interpolation", Signal Processing Letters, IEEE Vol: 14, Issue: 11 Pag:816-819, 2007.
  16. Aguilar Ponce, R.M. ; Jovanovic-Dolecek, G. "A multirate approach to design of fractional delay filters", Design of Mixed-Mode Integrated Circuits and Applications, 1999. Third International Workshop, Pag:143-146, 1999.
  17. Chien-Cheng Tseng,Soo-Chang Pei, "An efficient design of a variable fractional delay filter using a first-order differentiator", Signal Processing Letters, IEEE Vol: 10, Issue: 10, Pag:307-310, 2003.
  18. Chien-Cheng Tseng, "Design of variable fractional delay FIR filter using differentiator bank", Circuits and Systems, ISCAS 2002. IEEE International Symposium, Vol: 4, Pag:IV-421-IV-424, 2002.
  19. Chien-Cheng Tseng, "Improved design of fractional order differentiator using fractional sample delay", Circuits and Systems, ISCAS 2005. IEEE International Symposium, Pag:3713-3716, Vol. 4, 2005.
  20. Chien-Cheng Tseng, "Design of fractional order digital FIR differentiators", Signal Processing Letters, IEEE, Vol: 8 , Issue: 3, Pag: 77-79, 2001.
  21. Chien-Cheng Tseng, "Closed-Form Design of Half-Sample Delay IIR Filter Using Continued Fraction Expansion", Circuits and Systems I: Regular Papers, IEEE Transactions, Vol: 54, Issue: 3, Pag:656-668, 2007.
  22. Chien-Cheng Tseng,Su-Ling Lee, "Design of Wideband Fractional Delay Filters Using Derivative Sampling Method", Circuits and Systems I: Regular Papers, IEEE Transactions, Vol: 57, Issue: 8, Pag:2087-2098, 2010
  23. Chien-Cheng Tseng,Su-Ling Lee, "Design of variable fractional delay filter using expansions of hyperbolic functions", Communications and Information Technolo gies (ISCIT), International Symposium , Pag:300-305,2010.