ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Madhuri Bijjal1, Vidya Kulkarni2, Vibha Amboji3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Security is critical aspect in two-tiered wireless sensor network and it is twofold in nature i.e. preserving privacy and integrity. To preserve the privacy, intermediate tier i.e. storage node has to process encoded queries over encoded data without knowing the actual values of sensor collected data. To do this, we use Prefix Membership function. To preserve the integrity of query result, we have considered two different techniques Merkle Hash Tree and Neighbor Chaining and compared the performance of these two techniques.
Keywords |
| Integrity, privacy, range queries, sensor networks, Merkle Hash Tree, Neighborhood Chaining |
INTRODUCTION |
| Wireless sensor networks(WSN) can be defined as network of devices denoted as nodes that can sense the environment and communication the information gathered from the monitored field through wireless links. WSN have been widely deployed for various applications, such as environment sensing, building safety monitoring, earthquake prediction etc. In this, consider a two-tiered sensor network architecture in which storage nodes gather data from nearby sensors and answer queries from the sink of the network. The storage nodes serve as an intermediate tier between the sensors and the sink for storing data and processing queries. Storage nodes bring three main benefits to sensor networks. First, sensors save power by sending all collected data to their closest storage node instead of sending them to the sink through long routes. Second, sensors can be memory-limited because data are mainly stored on storage nodes. Third, query processing becomes more efficient because the sink only communicates with storage nodes for queries. The inclusion of storage nodes also brings significant security challenges. As storage nodes store data received from sensors and serve as an important role for answering queries, they are more vulnerable to be compromised, especially in a hostile environment. A compromised storage node imposes significant threats to a sensor network. First, the attacker may obtain sensitive data that has been, or will be, stored in the storage node. Second, the compromised storage node may return forged data for a query. Third, this storage node may not include all data items that satisfy the query. |
| Therefore, there is a need to design a protocol that prevents attackers from gaining information from both sensor collected data and sink issued queries, which typically can be modelled as range queries, and allows the sink to detect compromised storage nodes when they misbehave. For privacy, compromising a storage node should not allow the attacker to obtain the sensitive information that has been, and will be, stored in the node, as well as the queries that the storage node has received, and will receive. Note that we treat the queries from the sink as confidential because such queries may leak critical information about query issuers’ interests, which need to be protected especially in military applications. For integrity, the sink needs to detect whether a query result from a storage node includes forged data items or does not include all the data that satisfy the query. There are two key challenges in solving the privacy and integrity-preserving range query problem. First, a storage node needs to correctly process encoded queries over encoded data without knowing their actual values. Second, a sink needs to verify that the result of a query contains all the data items that satisfy the query and does not contain any forged data. |
MODELS AND PROBLEM STATEMENT |
| System Model |
| A two-tired sensor network consists of three types of nodes: sensors, storage nodes, and a sink. Sensors are inexpensive sensing devices with limited storage and computing power. They are often massively distributed in a field for collecting physical or environmental data, e.g., temperature. Storage nodes are powerful wireless devices that are equipped with much more storage capacity and computing power than sensors. Each sensor periodically sends collected data to its nearby storage node. The sink is the point of contact for users of the sensor network. Each time the sink receives a question from a user, it first translates the question into multiple queries and then disseminates the queries to the corresponding storage nodes, which process the queries based on their data and return the query results to the sink. The sink unifies the query results from multiple storage nodes into the final answer and sends it back to the user. |
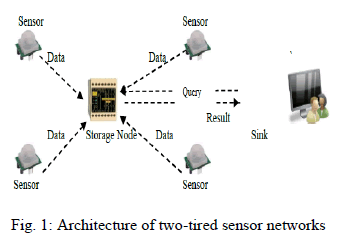 |
| For the above network architecture, assume that all sensor nodes and storage nodes are loosely synchronized with the sink. With loosely synchronization in place, we divide time into fixed duration intervals and every sensor collects data once per time interval. From a starting time that all sensors and the sink agree upon, every n time intervals form a time slot. From the same starting time, after a sensor collects data for n times, it sends a message that contains a 3-tuple (i, t, {d1, · · · , dn}), where i is the sensor ID and t is the sequence number of the time slot in which the n data items {d1, · · · , dn} are collected by sensor si. A range query “finding all the data items, which are collected at time slot t and whose value is in the range [a, b]” is denoted as {t, [a, b]}. Note that the queries in most sensor network applications can be easily modeled as range queries. |
| Menace Model |
| For a two-tiered sensor network, assume that the sensors and the sink are trusted, but the storage nodes are not. In a hostile environment, both sensors and storage nodes can be compromised. If a sensor is compromised, the subsequent collected data of the sensor will be known to the attacker, and the compromised sensor may send forged data to its closest storage node. However, the data from one sensor constitute a small fraction of the collected data of the whole sensor network. Therefore, we mainly focus on the scenario where a storage node is compromised. Compromising a storage node can cause much greater damage to the sensor network than compromising a sensor. After a storage node is compromised, the large quantity of data stored on the node will be known to the attacker, and upon receiving a query from the sink, the compromised storage node may return a falsified result formed by including forged data or excluding legitimate data. Therefore, attackers are more motivated to compromise storage nodes. |
| Problem Definition |
| The fundamental problem for a two-tired sensor network is the following: How to design the storage scheme and the query protocol in secured manner? Here in this context, security comes in two flavours such as privacy and integrity. A satisfactory solution to this problem should meet the following two requirements: |
| 1. Data and query privacy: |
| Data privacy means that a storage node cannot know the actual values of sensor collected data. This ensures that an attacker cannot understand the data stored on a compromised storage node. Query privacy means that a storage node cannot know the actual value of sink issued queries. This ensures that an attacker cannot understand, or deduce useful information from, the queries that a compromised storage node receives. |
| 2. Data integrity: |
| If a query result that a storage node sends to the sink includes forged data or excludes legitimate data, the query result is guaranteed to be detected by the sink as invalid. Besides these two hard requirements, a desirable solution should have low power and space consumption because these wireless devices have limited resources. |
PRIVACY PRESERVING SCHEME |
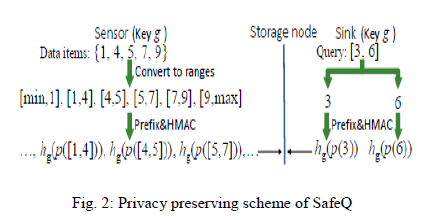
| To preserve privacy, each sensor si encrypts data items d1,…,dn using its secret key ki, denoted as (d1)ki ,... ,(dn)ki. Note that, ki is a shared secret key with the sink. However, the key challenge is how a storage node processes encrypted queries over encrypted data without knowing their values. The idea of our solution is to convert sensor collected data and sink issued queries to prefixes, and then use prefix membership verification[8][9] to check whether a data item satisfies a range query. |
| To prevent a storage node from knowing the values of data items and range queries, sensors and the sink apply Hash Message Authentication Code (HMAC)[6] to each prefix converted from the data items and range queries. For example, consider sensor collected data {1, 4, 5, 7, 9} and a sink issued query [3,7] in Fig. 2. The sensor first converts the collected data to ranges [min,1], [1,4], …. , [9,max], where min and max denote the lower and upper bound for all possible data items, respectively. Second, the sensor converts each range [dj, dj+1] to prefixes, denoted as p([dj , dj+1]), and then apply HMAC to each prefix in p([dj , dj+1]), denoted as hg(p([dj , dj+1])). Third, the sensor sends the result to a storage node. When the sink performs query [3,7], it first converts 3 and 6 to prefixes, denoted as p(3) and p(7), respectively, and then apply HMAC to each prefix in p(3) and p(7), denoted as hg (p(3)) and hg (p(6)), respectively. Upon receiving query hg (p(3)) and hg (p7)) from the sink, the storage node checks which hg(p([dj , dj+1])) has common elements with hg(p(3)) or Hg(p(7)). Based on prefix membership verification, if hg (p(a)) ∩ hg (p([dj , dj+1])) 6≠ ∅. , a ∈ [dj , dj+1]. Therefore, hg (p(3)) ∩ hg(p([1, 4])) 6≠ ∅. And hg (p(7)) ∩ hg (p([5, 7])) ≠ ∅.. Finally, the storage node finds that the query result of [3,7] includes two data items 4 and 5, and then sends (4)ki and (5)ki to the sink. |
 |
INTEGRITY PRESERVING SCHEME |
| The meaning of data integrity is two-fold in this context. In the result that a storage node sends to the sink in responding to a query, first, the storage node cannot include any data item that does not satisfy the query; second, the storage node cannot exclude any data item that satisfies the query. To allow the sink to verify the integrity of a query result, the query response from a storage node to the sink consists of two parts: (1) the query result QR, which includes all the encrypted data items that satisfy the query; (2) the verification object VO, which includes information for the sink to verify the integrity of QR. To achieve this purpose, we propose two schemes based on two different techniques: Merkle hash trees and neighborhood chains. |
| Merkle Hash Trees(MHT) |
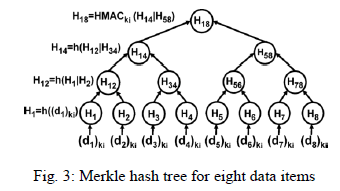
| Each time a sensor sends data items to storage nodes, it constructs a Merkle hash tree for the data items. Fig. 3 shows a Merkle hash tree constructed for eight data items. Suppose sensor si wants to send n=2m encrypted data items (d1)ki,.....(dn)ki to a storage node. Sensor si first builds a Merkle hash tree for the n=2m data items, which is a complete binary tree. The terminal nodes are H1…..Hn, where Hj=h((dj)ki) for every 1 ≤ j ≤ n . Function is a one-way hash function such SHA-1. |
| The value of each non terminal node v, whose children are vl and vr, is the hash of the concatenation of vl’s value and vr’s value. For example, in Fig.3, H12=h(H1|H2) . Note that if the number of data items n is not a power of 2, interim hash values that do not have a sibling value to which they may be concatenated are promoted, without any change, up the tree until a sibling is found. Note that the resulting Merkle hash tree will not be balanced. For the example Merkle hash tree in Fig. 3, if we remove the nodes H6, H7, H8, H78 and let H58 = H56 = H5, the resulting unbalanced tree is the Merkle hash tree for five data items. The Merkle hash tree used in our solution has two special properties that allow the sink to verify query result integrity. First, the value of the root is computed using a keyed HMAC function, where the key is ki, the key shared between sensor and the sink. For example, in Fig. 4, H18 = HMACki (H14 |H58) . Using a keyed HMAC function gives us the property that only sensor and the sink can compute the root value. Second, the terminal nodes are arranged in an ascending order based on the value of each data item. |
 |
| We first discuss what a sensor si needs to send to its nearest storage node along its data items dj. Each time sensor si wants to send encrypted data items to a storage node, it first computes a Merkle hash tree over the encrypted data items, and then sends the root value along with the n encrypted data items to a storage node. Note that among all the nodes in the Merkle hash tree, only the root is sent from sensor si to the storage node because the storage node can compute all other nodes in the Merkle hash tree by itself. |
| Next, can discuss what a storage node needs to send to the sink along a query result, i.e., what should be included in a verification object. For the storage node that is near to sensor , each time it receives a query [a,b] from the sink, it first finds the data items that are in the range. Second, it computes the Merkle hash tree (except the root) from the data items. Third, it sends the query result QR and the verification object VO to the sink. Given data items (d1)ki,.....(dn)ki in a storage node, where d1,…dn, and a range [a,b], where dn-1< a < dn1< …..< dn2 ≤ b < dn2+1 and 1 ≤ n1-1 < n2+1 ≤ n, and the query result QR= { (dn1)ki……{(dn2)ki}, the storage node should include and in the verification object VO= {(dn-1)ki, (dn+2)ki} because (dn-1)ki and (dn+2)ki ensure that the query result does include all data items that satisfy the query as the query result is bounded by them. Let’s call (dn-1)ki the left bound of the query result, and (dn+2)ki right bound of the query result. Note that the (dn-1)ki left bound and the (dn+2)ki right bound may not exist. If a <=d1, then left bound (dn-1)ki does not exist; if b <= dn, the right bound (dn+2)ki does not exist. The verification object includes zero to two encrypted data items and O(log n) proof nodes in the Merkel hash tree that are needed for the sink to verify the integrity of the query result. |
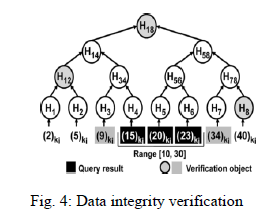
| Taking the example in Fig. 4, suppose a storage node has received eight data items { (2)ki, (5)ki, (9)ki, (15)ki, (20)ki, (23)ki, (34)ki, (40)ki } that sensor collected at time t, and the sink wants to perform the query [10,30] on the storage node. Using Theorem 4.1, the storage node finds that the query result includes (15)ki, (20)ki and (23)ki which satisfy the query. Along with the query result (i.e., the three data items), the storage node also sends (9)ki, (34)ki, H12, H8 and H18 which are marked gray in Fig.4.5, to the sink as the verification object. |
 |
| Next, we discuss how the sink uses Merkle hash trees to verify query result integrity. Upon receiving a query result and its verification object, the sink computes the root value of the Merkle hash tree and then verifies the integrity of the query result QR= {(dn1)ki……{(dn2)ki}. Query result integrity is preserved if and only if the following four conditions hold: |
| 1. The data items in the query result do satisfy the query. |
| 2. If the left bound (dn-1)ki exists, verify dn-1 < a that and (dn-1)ki is the nearest left neighbor of in the Merkle hash tree; otherwise, verify that (dn)ki is the leftmost encrypted data item in the Merkle hash tree. |
| 3. If the right bound (dn+2)ki exists, verify that b < dn+2 and (dn+2)ki is the nearest right neighbor of (dn2)ki in the Merkle hash tree; otherwise, verify that (dn2)ki is the rightmost encrypted data item in the Merkle hash tree. |
| 4. The computed root value is the same as the root value included in VO. |
| Note that sorting data items is critical in our scheme for ensuring the integrity of query result. Without this property, it is difficult for a storage node to prove query result integrity without sending all data items to the sink. |
| Neighborhood Chaining(NC) |
| A new datastructure to preserve integrity called neighborhood chains and then discuss its use in integrity verification. Given n data items d1, · · · , dn, where d0 < d1 < · · · < dn < dn+1, we call the list of n items encrypted using key ki, (d0|d1)ki , (d1|d2)ki , · · · , (dn−1|dn)ki , (dn|dn+1)ki, the neighborhood chain for the n data items. Here “|” denotes concatenation. For any item (dj−1|dj)ki in the chain, we call dj the value of the item and (dj |dj+1)ki the right neighbor of the item. Fig. 5 shows the neighborhood chain for the 5 data items 1, 3, 5, 7 and 9. |
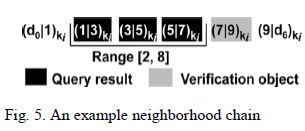 |
| Preserving query result integrity using neighborhood chaining works as follows. After collecting n data items d1, · · · , dn, sensor si sends the corresponding neighborhood chain (d0|d1)ki , (d1|d2)ki , · · · , (dn−1|dn)ki , (dn|dn+1)ki, instead of (d1)ki , · · ·, (dn)ki , to a storage node. Given a range query [a, b], the storage node computes QR as usual. The corresponding verification object VO only consists of the right neighbor of the largest data item in QR. Note that VO always consists of one item for any query. If QR = {(dn1−1|dn1 )ki , · · · , (dn2−1|dn2 )ki }, then VO = {(dn2 | dn2+1)ki }; if QR = ∅ , suppose dn2 < a ≤ b < dn2+1, then VO = {(dn2 |dn2+1)ki}. |
| After the sink receives QR and VO, it verifies the integrity of QR as follows. First, the sink verifies that every item in QR satisfies the query. Second, the sink verifies that the storage node has not excluded any item that satisfies the query. |
| Let {(dn1−1|dn1 )ki , · · ·, (dj−1|dj)ki , · · · , (dn2−1|dn2 )ki } be the correct query result and QR be the query result from the storage node. Let’s consider the following four cases: |
| 1. If there exists n1 < j < n2 such that (dj−1|dj)ki does not belong to QR, the sink can detect this error because the items in QR do not form a neighborhood chain. |
| 2. If (dn1−1|dn1 )ki does not belong to QR, the sink can detect this error because it knows the existence of dn1 from (dn1 |dn1+1)ki and dn1 satisfies the query. |
| 3. If (dn2−1|dn2 )ki does not belong to QR, the sink can detect this error because it knows the existence of dn2 from the item (dn2 |dn2+1)ki in VO and dn2 satisfies the query. |
| 4. If QR = ∅, the sink can verify this fact because the item (dn2 |dn2+1)ki in VO should satisfy the property dn2 < a ≤ b < dn2+1. |
| Note that our submission and query protocols are designed to facilitate integrity verification. To process query [a, b] over data items d1, · · · , dn, instead of testing whether each data item di is in [a, b], we test which ranges among [d0, d1], [d1, d2], · · ·, [dn, dn+1] contain a and which ranges contain b. Thus, a storage node not only can find which items satisfy a query, but also can find the right neighbor of the largest data item in the query result, which is the verification object. |
EXPERIMENTAL RESULTS |
| To get desired result, we need Pentium-4, genuine Intel, 2GB RAM, 40GB hard Disk, Windows XP/7,Eclipse indigo IDE, java language, MySQL database. |
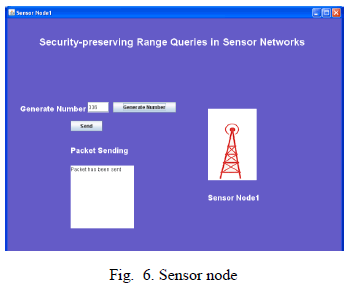 |
| Sensor node captures data, sends it to nearest storage node. We have simulated 4 sensor nodes in our experiment. |
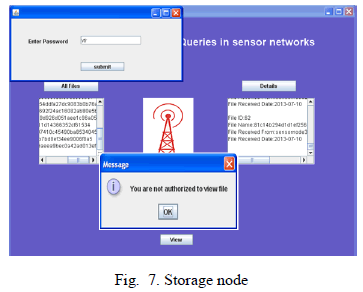 |
| Storage node cannot see the actual values of sensor collected data unless it enters the correct password. This ensures that an attacker cannot understand the data stored on a compromised storage node. By this it can preserves the privacy. |
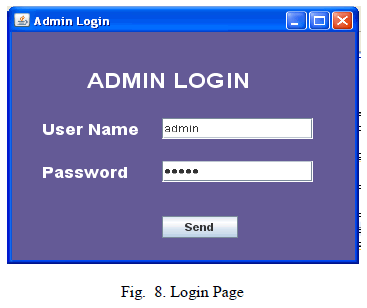 |
| From Login page, user can login to respected sink. Here we have given option to enter into sink which incorporates Merkle Hash Tree and sink which incorporates Neighborhood Chaining. |
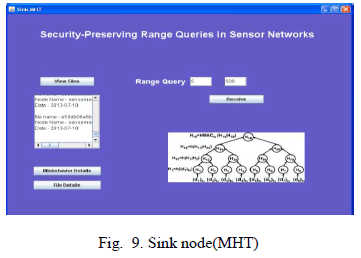 |
| Sink node, which incorporates Merkle Hash Tree(MHT) as to provide integrity for query result. Sink node can view the received files, misbehave details, file details. It can throw a range query to storage node. |
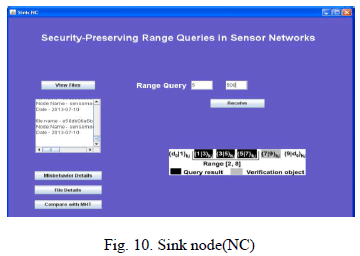 |
| Sink node(NC), which incorporates Neighborhood Chaining as to provide integrity for query result. This sink also does the same functionalities as that of sink which incorporates Merkle hash tree. |
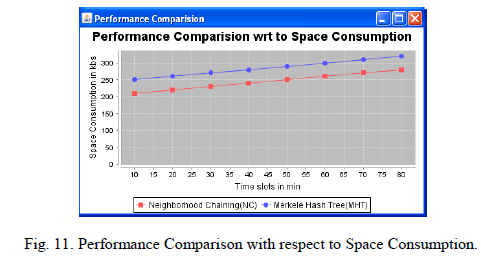 |
| Neighborhood Chaining consumes less space than Merkle Hash Tree. |
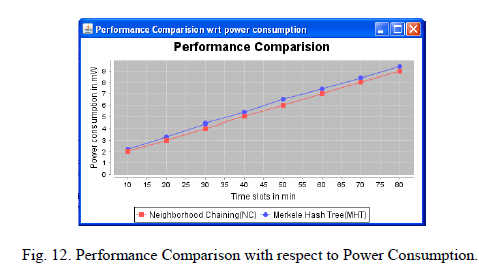 |
| Since Merkle Hash Tree does more computation than Neighborhood Chaining. So Merkle Hash Tree consumes more space than Neighborhood Chaining. So Neighborhood Chaining is better than Merkle Hash Tree. |
CONCLUSION AND FUTURE WORK |
| SafeQ preserves the Privacy and Integrity in two-tired sensor wireless sensor networks efficiently. SafeQ uses the techniques of prefix membership verification, Merkle hash trees, and neighborhood chaining. In terms of security, SafeQ significantly strengthens the security of two-tiered sensor networks. SafeQ prevents a compromised storage node from obtaining a reasonable estimation on the actual values of sensor collected data items and sink issued queries. SafeQ also allows a sink to detect compromised storage nodes when they misbehave. Neighborhood Chaining is better than Merkle Hash Tree in terms of storage space and power consumption. Future work on this thesis is to experiment SafeQ with multidimensional dimensional data. |
References |
|