ISSN ONLINE(2320-9801) PRINT (2320-9798)
ISSN ONLINE(2320-9801) PRINT (2320-9798)
| A.F Donfack Kana, A.B. Yusuf Department of Mathematics, Ahmadu Bello University, Zaria, Nigeria. |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering
This paper defines a method of achieving interoperability between description logics Ontologies through matching. The matching techniques used take into consideration the hierarchical and logical structure of Ontologies and suggest a one to one matching between the concepts of ontologies by analyzing the structural and logical definition of such concepts.
Keywords |
| Ontology, Description logics, Mapping, Interoperability |
INTRODUCTION |
| An ontology[14] is used to model an area of knowledge by clearly defining semantically the concepts in the given domain and the relationships among them without any ambiguity in such a way that it can be understood by humans and computers. Despite the standardization of various ontology languages, there is no standardization on how ontologies should be constructed. The direct consequence is that Ontologies are incompatible even those representing the same domain. Terminologies used in a particular Ontology may be ambiguous while interpreted by other Ontologies modeling the same domain. This leads to inconsistent interpretation and uses of knowledge across systems. Consequently, interoperability among Ontology systems is no longer possible at semantic level. Thus, Ontologies then face the same or even harder problems with respect to heterogeneity as any other piece of information [15]. Several research works have been undertaken in recent time to determine how Ontologies should be constructed and to attempt to overcome the problem of semantic interoperability. Description logics [1, 12] provide a logical approach in building Ontologies by using logical constructors and provide means of reasoning on their contents. Many review [2,3] show how description logics can be used in building Ontologies in order to resolve the ambiguity conflict between interpretation of terms and fail to show a clear way of how interoperability between them can be achieved. |
| Since there are many description logics languages and they differ from their syntax and their expressivity, and also there is no standardization on the Meta data (entities), one cannot assume a single Ontology for the same domain. It is evident that, different Ontologies builders can use different Meta data, to represent the same object or use different logical definitions (different in terms of syntax) to define the same object. The main objective of using Ontology to model a domain is to provide a common understanding of the domain being modeled. If Ontologies modeling the same domain cannot interoperate, we cannot really talk of common understanding. This limits the sharing of knowledge between different Ontologies. An approach to this problem is to determine a platform that reconciles different Ontologies. Literatures on how to reconcile different Ontologies remain scanty [18]. Mapping of the elements of Ontologies is often used as an attempt for that purpose. A review of existing systems for Ontology mapping reveal that most of the systems achieve semantic mapping by performing a deep analysis of syntactic comparison or by using class instance comparison[5,10,13]. The syntactic analysis may be done by referring to special dictionaries, by using a lexicon of synonyms terms or by any other technical decomposition of the meta data that can be helpful in finding their synonyms from one of the above techniques. In natural language, some Jargons used may not be easily interpreted so as to derive their syntactic similarities. It reveals that an analysis of description logics Ontologies based on the logical constructors used in defining concepts may be useful in solving such problems since they are natural language independent. This paper takes SHIQ as an example and describes a mapping approach, that relies mostly on the organization of logical operators that are used to define concepts to predict the semantic similarities between Ontologies. |
| The next section defines Ontology and classifies the type mismatches that can exist between Ontologies, section 3 gives a brief overview of SHIQ description logics and section 4 describes an approach of performing a logical mapping between description logics based Ontologies. |
ONTOLOGIES AND ONTOLOGIES MISMATCHES |
| Ontologies are specifications of a formal and common understanding of a domain, which tries to reduce the gap between the way in which humans and machines handle information [9]. Ontologies have a role in defining and relating concepts that are used to describe data. They are developed for knowledge sharing and reuse [11]. A core purpose of the use of Ontologies is the exchange of data not only at a common syntactic level, but also at a shared semantic level. Ontologies become a very important technology for the improvement of the exchange of knowledge. For example, in the World Wide Web, the use of Ontologies have begun to replace the old-fashioned ways of exchanging business data via standardized comma-separated formats by standard syntax (like XML/RDF) that adheres to semantic specifications given through Ontologies. However, the existence of a variety of views on an entity calls for efficient means for comparing two entities in order to enable the communication between two parties. However, determining these semantic mappings is a difficult task because of a variety of mismatches between Ontologies. |
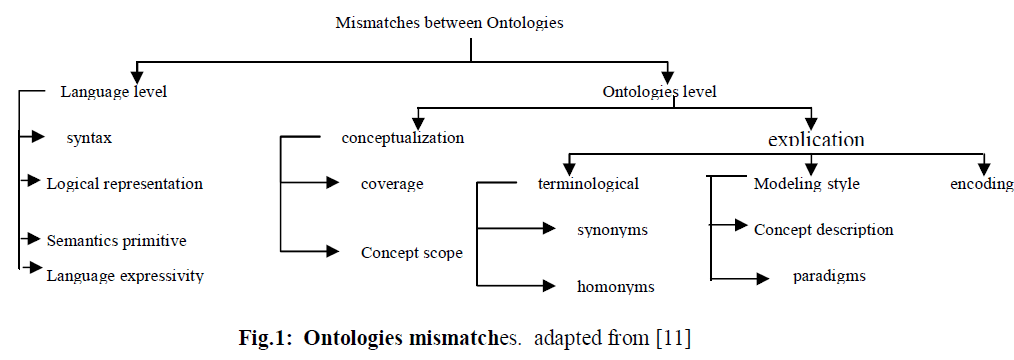
| Broadly speaking, differences between Ontologies modeling the same environment are found at two main levels: language level and Ontology level. |
 |
| There exists several Ontology languages that differ in their syntax and their expressiveness. Because of these differences, comparing Ontology in different languages becomes inadequate unless techniques are developed to bring the languages into a common interpretation of their syntax. |
| Differences between Ontologies modeling the same environment can occur whether the two Ontologies use the same language or not. [11] Classifies two levels at which mismatches can occur between Ontologies: The first level is at the language level where mismatches between Ontologies occur when Ontologies are written in different ontology languages. Mismatches between Ontologies at this level are due to heterogeneity between various Ontologies languages. This is due to mismatches between the languages syntax and their expressivity. Generally, different Ontologies languages always have some differences in their syntax. The same definition may appear differently in different languages. The logical construct allowed in one language may not be allowed in another language. The expressivity of language may cause some definition to be possible in some languages while the same definition may not be expressed in another language. For instance it is possible to represent the fact that someone has exactly two children using the cardinality restriction in SHIQ, SHOQ and many expressive Ontologies languages while such representation is not possible in ALC. Also, for some definitions, some languages have a direct constructor to represent the definition while for other languages, one must use a combination of several constructors to represent the same definition. |
| The second level is the ontology level. Mismatches at this level are viewed as the differences in the way the domain is modeled. Mismatches at the ontology level happen when two or more Ontologies that describe (partly) overlapping domains are combined. These mismatches may occur when the Ontologies are written in the same language, as well as when they use different languages. [17] classifies ontology level mismatches as conceptualization and explication mismatches of Ontologies and makes a clear distinction between the two mismatches. |
| A conceptualization mismatch refers to the differences in the way a domain is interpreted (conceptualized), which results in different ontological concepts or different relations between those concepts. An explication mismatch, on the other hand, refers to the differences in the way the conceptualization is specified. This results to the mismatches between terminologies used, in their definitions, mismatches in terms and combinations of both. [11, 16, 17] describe in detail differences between Ontologies. Figure 1 summarizes the differences that can be found between Ontologies. Whenever mismatches occur between Ontologies, one needs to compare Ontologies and find out to what degree they overlap and fit to each other in order to bring about a satisfying semantic interoperability. |
DESCRIPTION LOGICS |
| Description logics (DLs) are a family of knowledge representation formalisms which can be used to represent the terminological knowledge of an application domain in a structured and formally well-understood way. Well understood means that there is no ambiguity in interpreting their meaning by both humans and computer systems. They are characterized by the use of various constructors to build complex concepts from simpler ones, an emphasis on the decidability of key reasoning tasks, and by the provision of sound, complete and (empirically) tractable reasoning services[14]. Inference capability of DLs makes it possible to use logical deduction to infer additional information from the facts stated explicitly in an ontology[18]. |
| DLs are made up of the following components: Instances of objects that denote singular entities in our domain of interest, Concepts which are collections or kinds of things, Attributes which describe the aspects, properties, features, characteristics, or parameters that objects can have and Relations which describe the ways in which concepts and individuals can be related to one another. It is customary to separate them into three groups: assertional (ABox) axioms, terminological (TBox) axioms and relational (RBox) axioms. |
| ABox axioms capture knowledge about named individuals. |
| For example, Father(peter) is a concept assertion which asserts that peter is an instance of the concept Father. hasChild(Peter, Amina) is a role assertion which asserts that Peter is the parent of Amina TBox axioms describe relationships between concepts. For example, the general concept inclusion such as Mother ̢́ ̉ Parent which defines Mother as subsumed by the concept Parent. Figure2 defined in[3] shows a sample Tbox. |
 |
| RBox axioms refer to properties of roles. It captures interdependencies between the roles of the considered knowledge base. For example the role inclusion motherOf ̢́ ̉parentOf. An ontology is said to be satisfiable if an interpretation exists that satisfies all its axioms. When an ontology is not satisfied in any interpretation, it is said to be unsatisfiable or inconsistent. |
| An interpretation I = (ΔI , .I) consists of a set ΔI called the domain of I, and an interpretation function .I that maps each atomic concept A to a set A I ⊆ ΔI , every role R to a binary relation RI , subset of I x I and each individual name a to an element aI ïÃÆÃŽΔI. |
| There exist several DLs and they are classified based on the types of constructors and axioms that they allow, which are often a subset of the constructors in SROIQ. The description logic ALC is the fragment of SROIQ that allows no RBox axioms and only , ¬, ∃ and ∀ as its concept constructors. The extension of ALC to include transitively closed primitive roles is traditionally denoted by the letter S. This basic DL is extended in several ways. Some other letters used in DL names hints at a particular constructor, such as inverse roles I, nominals O(i.e., concepts having exactly one instance), qualified number restrictions Q, and role hierarchies H. So, for example, the DL named SHIQ is obtained from S by allowing additionally the role hierarchies, inverse roles and qualified number restrictions. The letter R most commonly refers to the presence of role inclusions, local reflexivity Self, and the universal role U, as well as the additional role characteristics of transitivity, symmetry, asymmetry, role disjointness, reflexivity, and irreflexivity [18]. Although DLs have a range of applications, OWL is one of its main applications. OWL is based on Description Logics but also features additional types of extra-logical information such as ontology versioning information and annotations [23]. The main building blocks of OWL are indeed very similar to those of DLs, with the main difference that concepts are called classes and roles are called properties[18]. |
| Large parts of OWL DL can indeed be considered as a syntactic variant of SROIQ. In many cases, it is indeed enough to translate an operator symbol of SROIQ into the corresponding operator name in OWL. |
MAPPING ONTOLOGIES |
| Given Ontologies O1 and O2, mapping Ontology O1 and O2 means that for each concept in Ontology O1, we try to find a corresponding concept, which has the same intended meaning, in Ontology O2. Mapping between concepts is the identification of maximal one to one correspondences between elements of the compared definitions is used as hint to identify the similarity between the given Ontologies. Mapping enables analysis of similarities and differences between the concepts to predict their semantic compatibility. |
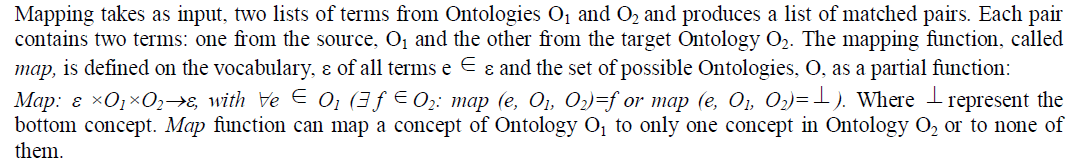 |
| For the sake of uniformity and ease of transformation of Ontologies into hierarchical tree, Ontologies to be mapped are defined in negation normal form (NNF), that is, negation occur only in front of concept names. Any SHIQ concept definition can be easily transformed to an equivalent one in NNF by pushing negations inwards using a combination of De Morgan’s laws and the following equivalences. |
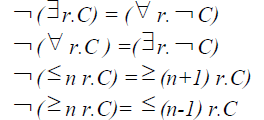 |
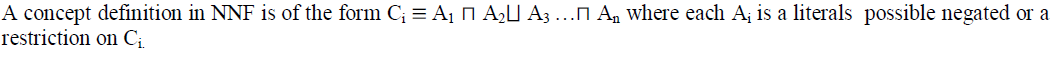 |
| For ease of comparison, one can adopt representing the Ontologies into hierarchical trees and then apply the graph matching techniques to traverse the two trees and computes the similarity between elements of the trees. With SHIQ General Concept Inclusion (GCI), which defines concepts by using their inclusion to another more general concept, Ontologies are translated into trees where concept of upper level of the tree, subsumes those beneath it. Ontologies are represented as a tree T= (N, E), where N is a finite set of nodes and E ïÃÆàN × N is a set of directed edges. Nodes of the tree represent the concept name and edge occurring between two nodes represents the role as well as associated constructors, which is the relation that links the two concepts. |
| Since concepts of higher level subsume those of the lower level, it implies that, the concepts of higher level are more generals (from their intended meaning) while the concept of the lower level of the hierarchy are more specific. The root of the tree is assumed to be the top concept and the leaves concepts are atomic concepts that do not subsumes any other concepts. |
| A. Ontologies matching |
| We compare the operators used in defining concept, which are the constructors in the role part of the definition for each sequence of rolei. To have a good understanding of the semantic of a particular defined concept, there is a need to understand the semantic of all other concepts associated in its definition. For example, if we define mother as follow: mother woman haschid.person. To capture the meaning of the concept mother, we need to understand first the meaning of woman and that of person as well as the relation haschild. We need then to refer to their own definition in order to deduce that of mother. Comparison here is performed not only on the concepts being compared, but also on the related concepts definition. |
| The semantics of concepts used in two Ontologies is captured based on three major key points: |
| Firstly, the concepts definitions, that is how the two concepts are defined, which type of operators and relations exist in the definition, what are the similarities between those operators and relations. This implies a comparison between definitions of the two concepts. It requires performing Cartesian comparison between all the rolei.concepti used in the definition of both concepts. |
| We deduce the similarities of two concepts by comparing the concepts that they subsume. Similar concepts will also subsume similar children concepts. Comparison is performed on all the definitions that uses each of the two concepts as parent concept. We compare all the edges departing from both concepts been compared. For two given concepts to be compared, we perform a total of Cartesian product of the number of children of each node. For each edge departing from the node of the concept being compared in the first Ontology, its best match is detected from all the edges of the node (concept) of the second Ontology. An average value is then defined from the ratio of all the best match value and the numbers of edges departing from the first concepts. The obtained value then gives the level of similarities on the way in which the two concepts subsume other concepts. |
| Thirdly, in a real world, two things are similar if they produce similar elements. Since Ontology is just a model of the real world, if two concepts are similar then it is likely that the concepts that they subsume may be similar or at least related in some way. For each pair of concepts being compared, we refer to how similar are their parents to predict their own similarities. |
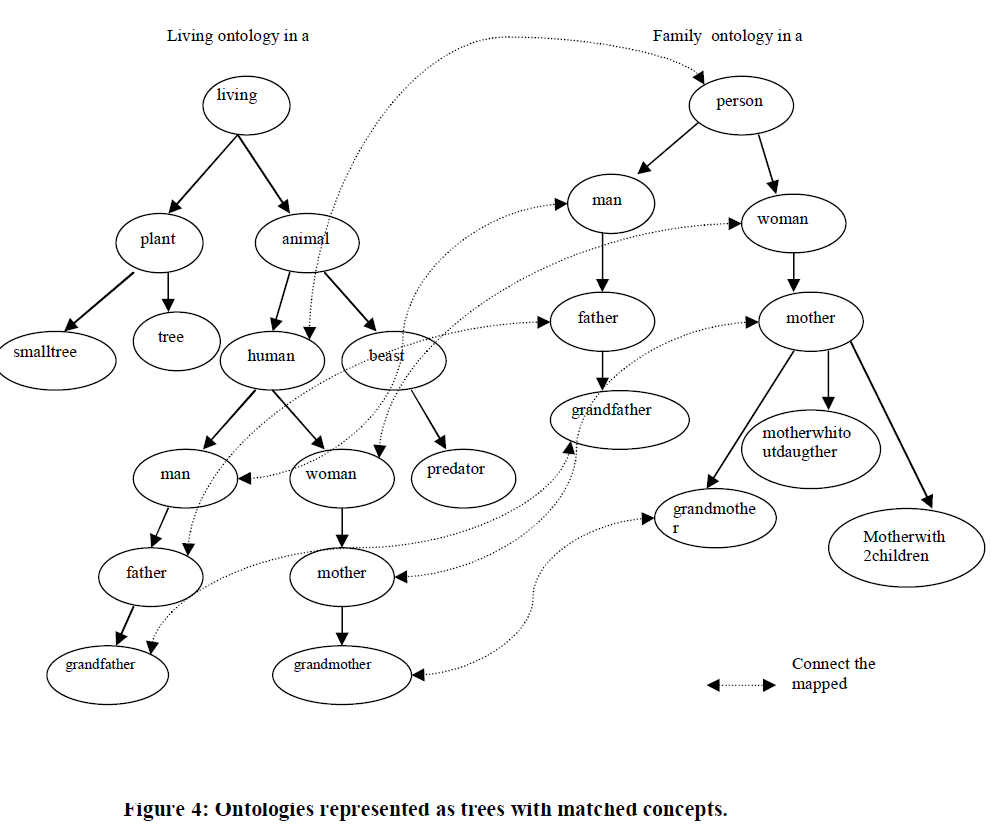
| For example, from the two Ontologies of figure3, the matching of figure 4 can be established |
 |
| Figure 4 shows two Ontologies transformed into hierarchical trees. Nodes are denoted with concepts. Edges represent the relationship between concepts.Given the two trees(figure 4), if mapping is to be performed between the concepts human in tree1 and man in tree2, then comparison will be done between the two concepts definition which is represented by the edges linking animal to human and the edge linking person to man.The similarity between their parent that is animal and person will be considered. The similarities between their successors, which is man and woman for the concept human and father for man. |
 |
B. Comparison techniques |
| Mapping is performed in a search space, where the two trees are traversed and nodes are recursively compared. We have adopted an approach that optimizes the comparison by reducing the total number of mapping to be performed. Nodes are compared only if there is a probability of them being similar. |
| Starting with two trees of m and n nodes respectively, the two trees are traversed simultaneously and performing the comparison of nodes elements and the related role elements. After all the nodes of the second tree have been compared with the root of the first tree, next nodes to be compared (except the root nodes) are selected based on the similarity of their ancestors. The decision on the similarity between pairs of node is performed locally. After the root node of the first tree is compared with all the nodes of the second tree, we can decide about its similarity with one of the nodes of the second tree. In case where one node of the second tree has been found to be similar with that of the currently selected node of the second tree, the next comparison is only performed in their successor. In the case where no similar node has been found for the current selected node, we assume that, the currently selected node has no similar node in the second tree and then, all its successors are compared with all the nodes of the second tree. |
| Any pair of compared nodes is treated as a candidate mapping that will be checked and the most similar concepts (if there exist) based on the similarity metric to be defined, is considered as the mapped concepts.The process is recursively performed until all nodes of the first tree are compared with all nodes of the second tree. |
C. Similarities evaluation |
| The similarity between the entities of the two Ontologies is defined as probable level at which the two elements are similar. We define a similarity measure for comparison of Ontology entities as a function as follows |
| Sim function returns a degree of similarity between pairs of concepts, which is a value between 0 and 1, where 1 stands for perfect match and zero for no match. |
| Similarity computation between an entity of Ontology O1 and an entity of Ontology O2 is performed using a wide range of similarity functions. To define the similarity functions, we define the general assumption about an Ontology representation and determine the feature of Ontology that will be useful in determining the similarity functions to measure the similarity between two entities of different Ontologies. The hierarchy structure of the tree, based on subsumption of concept implies that each concept was defined only once and thus appears only once on the graph. Based on that, it is likely that each entity on the first Ontology may only have at most only one similar concept in the second Ontology. This reduces then the task of mapping between two Ontologies to a one to one mapping between their respective concepts. |
| SHIQ Ontology is defined using concept name, role name that is a relation occurring between concepts and possibly constraints on this relation, as well as constructors to combine those concepts. Different comparison is performed for each elements of the tree. |
| For each pair of concept being compared, a logical comparison is performed on the logical symbols that associate the concepts to their neighbor. This comparison is associated a weight which defines the importance of the logical operators in determining the similarities of the concepts being defined. Because theses operators do not have any relation with the language used, they are considered to be the main point at which the comparison is based upon. Their comparison is then based on a direct logical comparison. Our mapping approach is to make the mapping as free as possible from the syntactic comparison. We assign a high weight to the logical comparison of logical constructors used in the definition. |
| Whenever there is a need, generally when Ontologies are built in the same natural language, syntactic comparison may be used to support the logical comparison but with a very low weight this syntactic comparison may be performed on Meta data used as concepts name or role label. Two identical terms, that is, having the same syntax and if they are used the same context, may have the same meaning. While modeling the same world using the same language, it will be difficult to find that knowledge modelers have used totally different vocabulary to define all of their concepts and role. Generally, they may choose the same concept name to represent the same things or different concepts name but highly syntactically related to represent the same things. For example, one may decide to use “studentname” to represent the student name while another builder may use “student_name” for the same purpose. The edit distance (ed) introduced by Levenshtein is used as a basic measure for similarity function. The idea behind this edit distance is to measure the minimum number of token insertions, deletions, and substitutions required to transform one string into another. Implementation of our edit distance is based on the longest common subsequence between two strings. The difference between two strings can easily be obtained from the longest common subsequence by subtracting the double of the length of the LCS from the sum of the length of the two strings. Edit distance is thus defined as: |
| Ed(string1,string2) = |string1|+|string2|-2(|LCS(string1,string2)|) |
| Ed is then a symmetry function. That is ed(string1, string2) = ed(string2,string1) |
| Based on that edit distance, we define the syntactic similarity function as a maximum value between 0 and the ratio of the minimum value between the length of the two strings, string1, and string2 minus their edit distance over the minimum length of the two strings. |
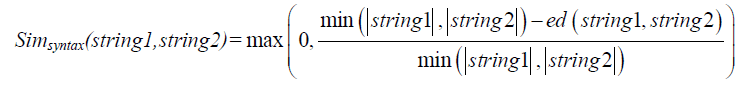 |
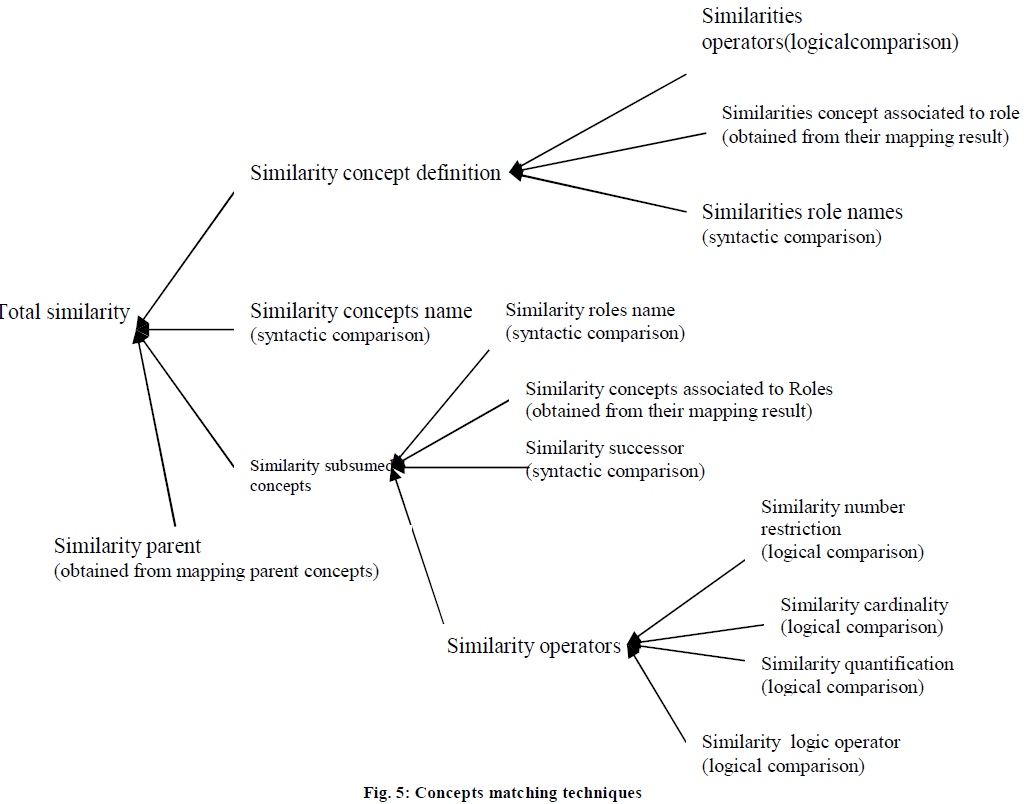
| Simsyntax function returns a degree of similarity of two strings, which is a value between 0 and 1, where 1 stands for perfect match and zero for bad match. It considers the number of changes that must be made to transform one string into the other and weights the number of these changes against the length of the shorter of the two strings. Figure 5 shows all the comparisons performed for a given pair of concepts to deduce their similarities |
 |
D. Similarity Aggregation. |
| The comparison gives several similarity values for a candidate pair of concepts from the two Ontologies O1, O2. These values are obtained from the computation of the similarity of concepts parent, the similarities of concepts definition and the computation of the similarity of their subsumed concepts. We define an aggregate value that gives the similarity value for that mapping. These values are assigned different weights that represent the importance for each of those above obtained value, to influence the final similarity value. We define the result of similarity between two concepts as follow: |
| Weight parent(score parent)+ weight concept definition(score concept definition )+weight concepts subsumption(score concept subsumption) / total weight (3.1) |
| Syntactic comparison, ( refers to fig 4 ) should be avoided whenever the two Ontologies are not in the same natural language. We analyze the similarity based only the symbols (constructors). This implies that the score of the concepts definition and that of the subsumed concepts will mainly depend on the logical constructors alone. (It will no longer take into account any syntactic comparison) |
E. Interpretation |
| The mapping between concepts of Ontology O1 and concepts of Ontology O2 provides a tabular representation of the entire possible mapping and their similarity values obtained from the similarity calculation. These values are used to derive mapping between concepts from Ontologies O1 and O2. Each table entry contains the two concepts been compared and the score of their similarity. |
| since each concept appears only once in the graph, each concept in Ontology O1 can only have at most one similar concept in Ontology O2. We define the threshold value, which gives the minimum value at which two concepts can be seen as being similar. Since the score of similarity between concepts is in the range of 0 to 1, where 1 stands for the perfect match and 0 for the bad match, the threshold is then chosen as a positive value between 0 and 1. This threshold defines the level at which, two concepts can be said to be semantically similar. |
| The entire table is scanned to determine the table entry having the highest value. The corresponding concepts are seen to be the most similar concepts. Their value is compared with the threshold value. If that value is greater than that of the threshold, then they are taken to be the most similar concepts. For each table entry having one of the two concepts, they are removed from the table and therefore no other concept can be mapped to them. The process is iterated until no value of similarity obtained is above the threshold value. |
CONCLUSION |
| This paper describes a matching technique for interoperability between SHIQ Ontologies. Hierarchical trees representing the source ontologies are constructed where nodes represent concepts and edges represent roles. The similarities between concepts is evaluated based not only on the syntax of concepts and role but puts more emphasis on hierarchical structure of the ontologies. The proposed approach is hoped to provide a framework towards a solution to the interoperability problem in order to facilitate exchange of knowledge between Ontologies. |
References |
|