ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Reenu George1, S. Kanthalakshmi2, Manoj G3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper describes simple position control of sensorless hybrid stepper motor (HSM). A mathematical model for hybrid stepper motor is derived using mechanical and electrical equations, which is used to estimate the position of the motor using Extended Kalman Filter (EKF). In position control, estimated value is compared with the reference position and when both coincide, the motor is held at a particular position for specified time and brought back to original position. The simulation results are presented.
Keywords |
| Hybrid stepper motor (HSM), Extended Kalman Filter (EKF), position control, sensorless. |
INTRODUCTION |
| Stepper motors find several applications in varying fields such as robotics, computer peripherals, business machines, machine tools etc. Off late, the use of stepper motors has seen a surge mainly attributed to their precision, robustness, reliability, smaller size and lower cost. Stepper motors were originally designed to be used in open loop control. Their inherent stepping ability allows for accurate positioning without feedback. However, they show a poor performance with respect to very precise motion control and high dynamic requirements. Closed loop control of stepper motors has been increasingly employed to achieve faster response times and higher resolution capabilities. Initially, mechanical sensors were used to introduce closed loop control of stepper motor; but it led to the increase in size and cost of the system. Therefore, sensorless control of stepper motors emerged as an alternative and attractive solution since it saves the expensive and bulky mechanical sensor. |
| Several sensorless methods have been proposed for motors that can be applied to the stepper motor. C. Obermeier [1] implemented sensorless field oriented speed control using an EKF for a permanent magnet stepper motor.Ferrah, Bani- Younes, Bouzguenda, and Tami [2] described the use of full orderEKF for sensorless speed and position estimation of two phase steppermotor. Bendjedia, Ait-Amirat, Walther, and Berthon [3] estimated rotor position, speed, and loadtorque using steady-state EKF and state feedback control for positioncontrol. |
| Usually, sensorless control is defined as a control scheme where no mechanical parameters like speed and torque are measured. Traditional vector control systems use the method of flux and slip estimations based on measurements of the phase currents and DC link voltage of the inverter, but this has a large error in speed estimation particularly in the low-speed range. There are two forms for the implementation of an estimator as open loop and closed loop. The difference between these two is a correction term, involving the estimation error, used to adjust the response of the estimator. A closed loop estimator is referred to as an observer. An observer can be classified according to the type of representation used for the plant to be observed. If the plant is deterministic, then the observer is a deterministic observer; otherwise it is a stochastic observer. The Luenberger observer is of the deterministic type and the Kalman Filter is stochastic type. |
| The Kalman filter [4] is applicable to linear stochastic systems, and for nonlinear systems, EKF can be used, which can provide estimates of the states of a system or estimates of both the states and system parameters. EKF [5] is a recursive filter (based on the knowledge of statistics of both the state and noise created by measurement and system modeling), which can be applied to non-linear time varying stochastic systems. Since EKF is more insensitive to parameter changes and can be used for stochastic systems (measurement and modeling noises taken into consideration), it is preferred for motor control application. EKF [2] is an estimator used to identify the speed and rotor position based on measured quantities such as current or voltage. |
| This paper is mainly focused on position control of HSM without use of an encoder. The system under study is a twophase HSM whose characteristics are analysed to find whether it is a linear or a nonlinear system. The mathematical model for HSM is derived using mechanical and electrical equations. Microstepping [6] is used to drive the stepper motor which has various advantages. The voltage input applied to the motor is in the form of sine and cosine. The system described here is a nonlinear system. EKF is used to estimate the states of the system. The measured current across the resistor gives the winding voltage and is used with EKF to reconstruct the states of motor. Estimation error is calculated to check the effectiveness of EKF. The estimated value is compared with the reference position and when both coincide, the motor is held at that particular position for specified time and then the motor is stopped. |
DYNAMIC MODELLING OF A STEPPER MOTOR |
| A model [1] has to be created in order to investigate the dynamics of mechanisms driven by stepper motors. This section provides a brief derivation of a nonlinear model of the two phase HSM represented by the following electrical and mechanical equations. |
 |
| where iaand ib are the currents of phase A and phase B (Amp), Ua and Ubare the voltages on phases A and B (Volt), R is the phase resistance (Ω), L is the phase inductance (H), Kmis the torque constant (V.s/rad), ω is the angular velocity (rad/s), θ is the mechanical rotor position (rad), N is the number of rotor teeth, Kv is the coefficient of viscous friction (N.m.s/rad), J is the system inertia (kg.m2) and TL is the load torque (N.m). |
| For control purpose, the differential equations are transformed into the rotor-fixed d-q coordinate frame by applying the Park Transformation. The model of HSM in rotating frame (d, q) is represented using the following equations. |
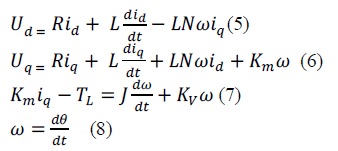 |
| The model parameters taken for standard benchmark problem [6] are, R = 0.37(Ω), L = 0.9(mH), Km = 0.157(V.s/rad),Kv= 0.000307(N.m.s/rad), J = 15.62 x 10-5(kg.m2), and N = 50. The discrete system model in the state space form for the model of HSM in rotating frame is represented by the following equation |
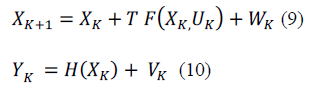 |
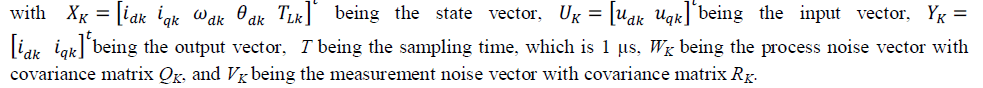 |
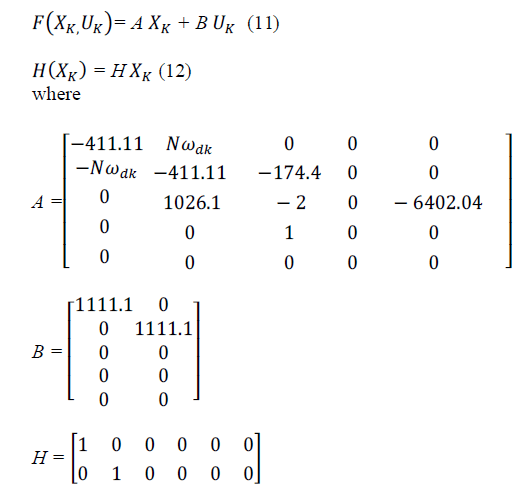 |
STATE ESTIMATION USING KALMAN FILTER |
| R.E. Kalman described a recursive solution to the discrete data linear filtering problem. Theoretically, Kalman filter (KF) is an estimator for what is called the linear-quadratic Gaussian problem, which is the problem of estimating the instantaneous state of a linear system from a measurement linearly related to the state but corrupted by Gaussian white noise. The resulting estimator is statically optimal with respect to any quadratic function of estimation error. From the mathematical point view, KF is a set of equations that provides an efficient recursive computational solution of the least square method. The filter is very powerful in that it provides estimation of the past, the present and the future states. This is achieved even when precise characteristics of the modelled system are unknown. KF is an extremely effective and versatile procedure for combining noisy sensor outputs to estimate the state of the system with uncertain dynamics. |
| In practical applications, many dynamic systems and sensors are not absolutely linear. Therefore, standard KF will not be suitable to estimate the system. EKF is a recursive optimum state-observer that can be used for the state and parameter estimation of a non-linear dynamic system in real time by using noisy monitored signals. This assumes that the measurement noise and system noise are uncorrelated. The noise sources take account of measurement and modelling inaccuracies. In the first stage of the calculations, the states are predicted by using a mathematical model (which contains previous estimates) and in the second stage, the predicted states are continuously corrected using a feedback correction scheme. This scheme makes use of actual measurements by adding a term to the predicted states (which is obtained in the first stage).The additional term contains the weighted difference of measured and estimated output signals. Based on the deviation from the estimated value, the EKF provides an optimum output value at the next input instant. |
| EKF algorithm has two distinct phases, the prediction phase represented by |
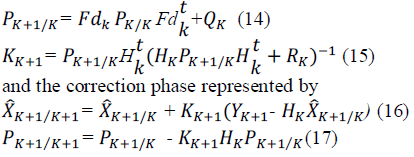 |
| whereK is the Kalman gain matrix, P is the covariance matrix, Fdk is the Jacobian matrix of the system and Hkis the Jacobian matrix of the output. |
POSITION ESTIMATION AND CONTROL USING EKF |
| In the present work, EKF is applied to estimate the position of two phase HSM using current measurement. The Jacobians of the dynamic stepper model is described by the following. Jacobian matrix of the system is given by |
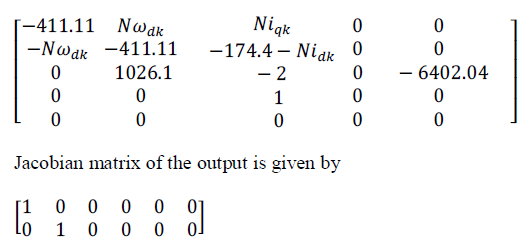 |
| Using the EKF algorithm given by (13) through (17), position estimator was implemented in Matlab. For estimation, the initial covariance matrix [6] is given by |
 |
| In the present work, when the rotor reaches a desired position, the position is maintained for a particular position for a desired time and then back to the original starting position. EKF is used to determine the desired position. At desired position a constant excitation is given to maintain the rotor position and then bringing the rotor to original position by reversing the excitation. |
SIMULATION RESULTS |
| In this work, sensorless technique for position control of stepper motor using Extended Kalman Filter has been developed. The system using the proper system model and input is simulated in Matlab. The motor is driven by applying the test input in the form of sine and cosine waves with given motor parameters. |
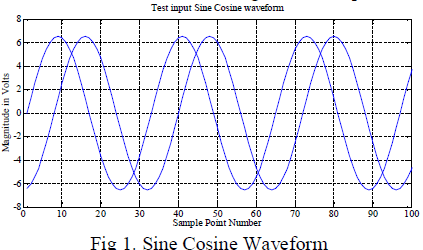 |
| In figure 1, the test input sine cosine waveform for driving the stepper motor is shown. |
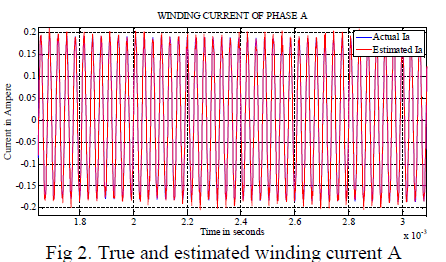 |
| In figure 2, the true and estimated values of winding current in phase A is shown, which looks like smooth sine waves. |
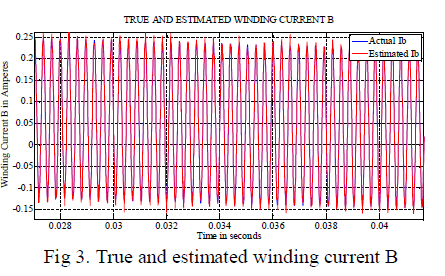 |
| In figure 3,the true and estimated values of winding current in phase B is shown. The error between true and estimated is in the order of 10-4. |
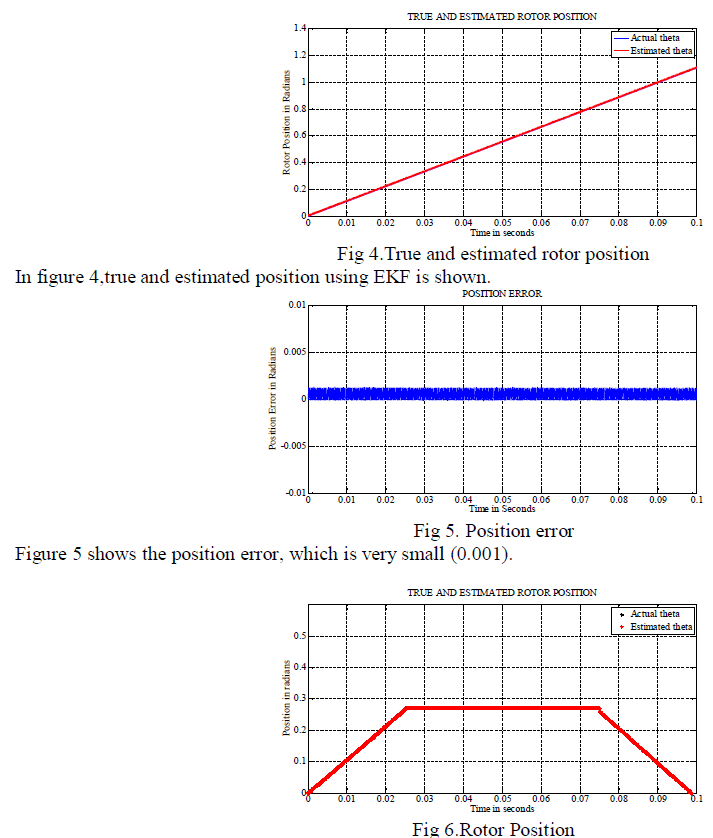 |
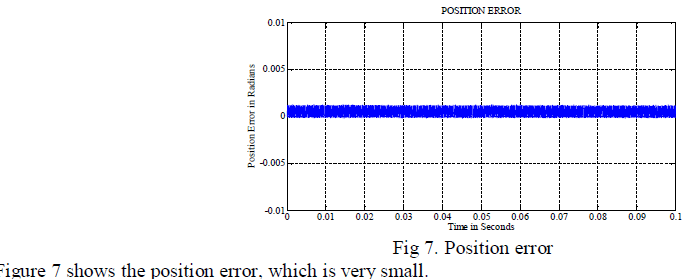
| Figure6 shows controlled true and estimated position response. The desired position is 150 and it is maintained for 0.06 sec and then motor is brought to original position. |
 |
CONCLUSION |
| In the present work, sensorless position control of a hybrid stepper motor was simulated. A dynamic mathematical model of the stepper motor was derived and formulated into state space model for easy analysis. Extended Kalman Filter was applied to the developed motor model. The model, which is inherently non-linear, was linearized prior to the EKF application. Simulation results showed good agreement between true and estimated states. The desired position estimated by EKF was maintained for a specified time and brought back to the original position. As future work, a suitable controller like fuzzy control technique, neural network control, active disturbance rejection control technique, or other optimized control technique may be implemented for position control. To estimate the motor parameters, particle filter or other non-linear filter techniques can be adopted. Finally, EKF with online computation of Kalman gain by switching to hardware based filtering or a fast microcontroller or DSP or other non-linear filter techniques may be implemented. |
References |
|