ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
| Shervin Samimian Tehrani1, Peyman Salmanpour Bandaghiri2 Student, Amirkabir University of Technology, Tehran Polytechnic, Iran |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Voltage stability of a system is affected by reactive power limit of the system. FACTs devices improve the reactive power flow in system thereby improving voltage stability and these are used for controlling transmission voltage, Power flow, dynamic response and reducing reactive losses in transmission lines. This paper explores the effect of SVC on static voltage stability and presents the effect of Static VAR compensator (SVC) on Voltage Profile & Reactive Power for variable load conditions is investigated and presents static methods like Modal Analysis, Two Bus Thevenin Equivalent and Continuation Power Flow methods to predict the voltage collapse of the bus in the power system. WSCC 3-machine, 9-bus system has been used to demonstrate the ability of SVC in improving the voltage stability margin. These FACTs controllers help to increase the load ability margin of the power network. Modelling & simulation have been carried out using MATLAB/SIMULINK Software.
Keywords |
| FACTS, SVC, Voltage Stability. |
INTRODUCTION |
| Today’s changing electric power systems create a growing need for flexibility, reliability, fast response and accuracy in the fields of electric power generation, transmission, distribution and consumption. Flexible Alternating Current Transmission Systems (FACTS) are new devices emanating from recent innovative technologies that are capable of altering the voltage, phase angle and/or impedance at particular points in power systems. Their fast response offers a high potential for power system stability enhancement apart from steady-state flow control. Among the FACTS controllers, Static Var Compensator (SVC) provides fast acting dynamic reactive compensation for voltage support during contingency events which would otherwise depress the voltage for a significant length of time. The important operating tasks of power utilities are to keep voltage within an allowable range for high quality customer services. Increase in the power demand has been observed all over the world in recent years. The existing transmission lines are being more and more pressurized. Such systems are usually subjected to voltage instability; sometimes a voltage collapse. Voltage collapse has become an increasing threat to power system security and reliability. The voltage stability is gaining more importance nowadays with highly developed networks as a result of heavier loadings. Voltage instability may result in power system collapse. Voltage stability is the ability of power system to maintain steady acceptable voltages at all buses in the system under normal conditions [1]. Voltage collapses the process by which the sequence of events accompanying voltage instability leads to a low unacceptable voltage profile in a significant part of the power system [2]. The main symptoms of voltage collapse are low voltage profiles, heavy reactive power flows, inadequate reactive support, and heavily loaded systems. The consequences of collapse often require long system restoration, while large groups of customers are left without supply for extended periods of time.The voltage stability problem is associated with reactive power and can be solved by providing adequate reactive power support to the critical buses. The control of reactive power of a switched capacitor bank is usually discrete in nature. Recent trend is to replace the switched capacitor banks by SVC to have a smooth control on reactive power. SVC has the capability of supplying dynamically adjustable reactive power within the upper and lower limits [3]. In the normal operating region, a SVC adjusts its reactive power output to maintain the desired voltage. For such an operation, the SVC can be modeled by a variable shunt susceptance. On the other hand, when the operation of the SVC reaches the limit, it cannot adjust the reactive power anymore and thus can be modeled by a fixed shunt susceptance. There are many methods currently in use to help in the analysis of static voltage stability. Some of them are PV analysis, QV analysis, Fast Voltage Stability Index (FVSI), multiple load flow solutions based indices, voltage instability proximity indicator [4], Line stability index, Line stability Factor, Reduced Jacobian Determinant, Minimum Singular Value of Power Flow Jacobian, and other voltage indices methods. The minimum singular value of the load flow Jacobian matrix is used as an index to measure the voltage stability limit is considered by reference [5]. Energy method [6, 7] and bifurcation theory [8] are also used by some researchers to determine the voltage stability limit. Point of collapse method and continuation method are also used for voltage collapse studies [9].Of these two techniques continuation power flow method is used for voltage analysis. These techniques involve the identification of the system equilibrium points or voltage collapse points where the related power flow Jacobian becomes singular [10, 11]. In this paper the following methods are used |
| 1. Modal Analysis method is used to identify the weak bus by calculating participation factors and sensitivity factors. |
| 2. Two Bus Thevenin Equivalent method is used to determine the maximum loading capability of a particular load bus in a power system through the Thevenin equivalent circuit and also the loading capability of the bus after the placement of SVC device. |
BASIC CONFIGURATION OF SVC |
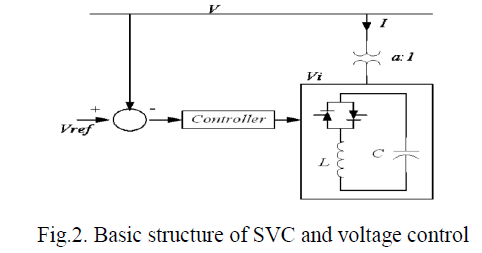
| The SVC uses conventional thyristors to achieve fast control of shunt-connected capacitors and reactors. The configuration of the SVC is shown in Fig.1, which basically consists of a fixed capacitor (C) and a thyristor controlled reactor (L). The firing angle control of the thyristor banks determines the equivalent shunt admittance presented to the power system. A shunt connected static Var generator or absorber whose output is adjusted to exchange capacitive or inductive current so as to maintain or control bus voltage of the electrical power system. Variable shunt susceptance model of SVC [12] is shown in Fig.1. |
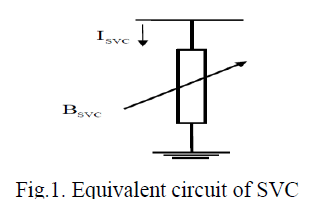 |
| As far as steady state analysis is concerned, both configurations can modeled along similar lines, The SVC structure shown in Fig. 1 is used to derive a SVC model that considers the Thyristor Controlled Reactor (TCR) firing angle as state variable. This is a new and more advanced SVC representation than those currently available. The SVC is treated as a generator behind an inductive reactance when the SVC is operating within the limits. The reactance represents the SVC voltage regulation characteristic. The reason for including the SVC voltage current slope in power flow studies is compelling. The slope can be represented by connecting the SVC models to an auxiliary bus coupled to the high voltage bus by an inductive reactance consisting of the transformer reactance and the SVC slope, in per unit (p.u.) on the SVC base. A simpler representation assumes that the SVC slope, accounting for voltage regulation is zero. This assumption may be acceptable as long as the SVC is operating within the limits, but may lead to gross errors if the SVC is operating close to its reactive limits [12].is operating close to its reactive limits [12]. The current drawn by the SVC is, ISVC jBSVC .VK |
| The reactive power drawn by SVC, which is also the reactive power injected at bus k is, |
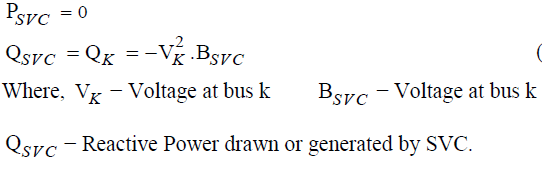 |
| The working principle of SVC element formed by using semi-conductors is based on providing shunt impedance by mounting and un-mounting of capacitors and/or reactors to and from the network according to calculated trigger angles. With the appropriate trigger, reactive power adjustments are possible in a wide range from maximum capacitive reactive power value to maximum inductive reactive power value in the bus that the static Var generator is connected [13]. Inductance determines the capacitive or inductive working positions of the device. The inductance value is calculated with the equation (2) below [14]: |
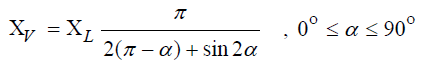 |
| Where, XL is thyristor uncontrolled basic inductive reactance and α is the trigger angle. Total impedance of the controller is calculated with the equation (3) below: |
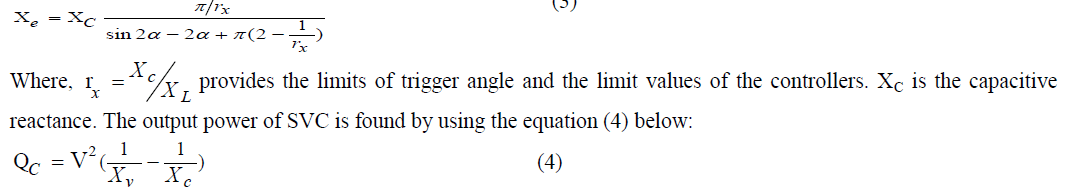 |
| Where, Vis the voltage of the line. |
| As the reactive power demand at the bus varies, the susceptance is varied subject to the limits. However, the reactive power is a function of the square of the bus voltage. Hence the reactive power generated decreases as the voltage decreases.The SVC can both absorb as well as supply reactive power at the bus it is connected to by control of the firing angle of the thyristor elements. By controlling the firing angle α of the thyristors (i.e., the angle with respect to the zero crossing of the phase voltage), the device is able to control the bus voltage magnitude. Changes in α results in changes on the current and hence, the amount of reactive power consumed by the inductor. When α = 90°, the inductor is fully activated but is deactivated when α = 180°. Actually, the basic control strategy is typically to keep the transmission bus voltage within certain narrow limits defined by a controller droop and the firing angle α limits (90° < α < 180°). |
 |
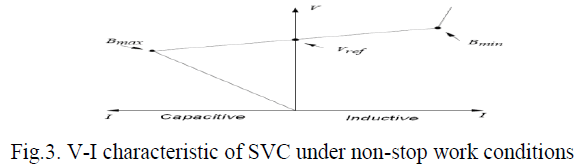
| Fig. 3 provides the voltage control characteristic of SVC in continuous operations [15]. Where, Vref shows the voltage value of the system under normal loading conditions. Bmax shows the inclusion of all capacities whereas Bmin shows the exclusion of all capacities. The flow to the system is either inductive or capacitive according to these conditions. In this system SVC controls the power system to which it is connected by behaving as an adjustable reactive power system. |
 |
NEWTON-RAPHSON METHOD |
| The Newton-Raphson method is widely used for solving non-linear equations. ultimately used to study power flow studies in power system. It transforms the original non-linear problem into a sequence of linear problems whose solutions approach the solutions of the original problem. Let G=F(x,y) be an equation where the variables x and y are the function of arguments of F. G is a specified quantity. |
| If F is non-linear in nature there may not be a direct solution to get the values of x and y for a particular value of G. in such cases, we take an initial estimate of x and y and iteratively solve for the real values of x and y until the difference is the specified value of G and the calculated value of F (using the estimates of x and y) i.e. ΔF is less than a tolerance value. The procedure is as follows: Let the initial estimate of x and y be o x and o y respectively. |
| Using Taylor series |
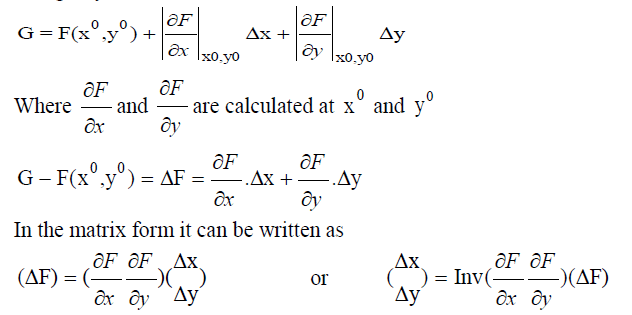 |
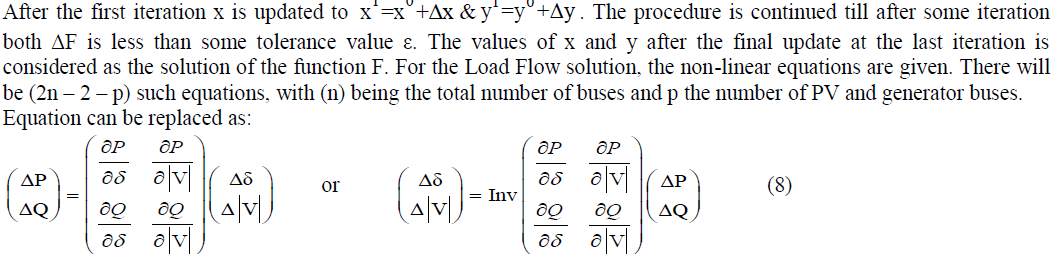 |
| The matrix of equation consisting of the partial differentials, is known as the Jacobean matrix and is very often denoted as J.ΔP is the difference between specifies value of P (Psp) and the calculated value of P using the estimates of δ and |V| in a previous iteration. We calculate ΔQ similarly.The Newton power flow is the most robust power flow algorithm used in practice. However, one drawback to its use is the fact that the terms in the Jacobian Matrix must be recalculated each iteration, and then the entire set of linear equations in equation must also be resolved each iteration. Since thousands of complete power flow are often run for planning or operations study, ways to speed up this process were devised.3.1. Two Bus Thevenin Equivalent Method . 3.1.1. Without Placement of SVC |
 |
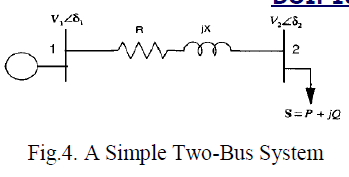 |
| For a given value of V1 the relationship between the load voltage magnitude V2 and the load power S = P +jQ can |
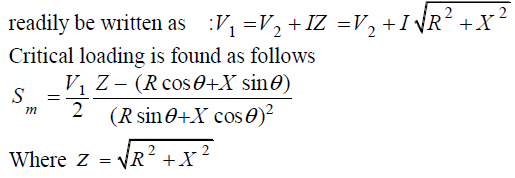 |
| The maximum reactive power loading Q m (with P = 0) and the corresponding voltage can be obtained from the above equations by setting θ = 0. |
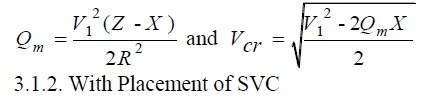 |
| A Simple and direct method of determining the steady state voltage stability limit of a power system after the placement of Static Var Compensator (SVC) is presented in reference [17].A SVC of finite reactive power rating is placed at the load center in two bus equivalent model and it is shown in fig. 5. |
 |
| The receiving end voltage decreases as the load increases and reactive power will be injected by SVC to boost the voltage. Voltage collapse occurs when there is further increase in load after SVC hits its maximum limit. In order to prevent voltage collapse, SVC is considered as fixed susceptance BC.Receiving end current from fig.5 is given by |
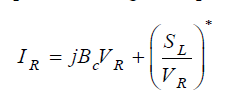 |
IMPLEMENTATION OF SVC ON WSC 3-MACHINE, 9-BUS SYSTEM |
| In this paper, the modeling is done in MATLAB/SIMULINK software tool. It consists of two Generator buses. Usually bus no.1 is considered as slack bus. |
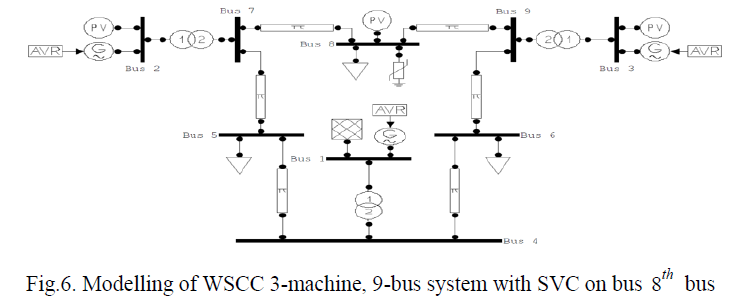 |
| First of all, a continuous power flow analysis for 9 bus system power system was undertaken in order to determine the maximum loading parameters without the use of SVC. Later, the most vulnerable bus of the system in terms of system voltage stability was determined. |
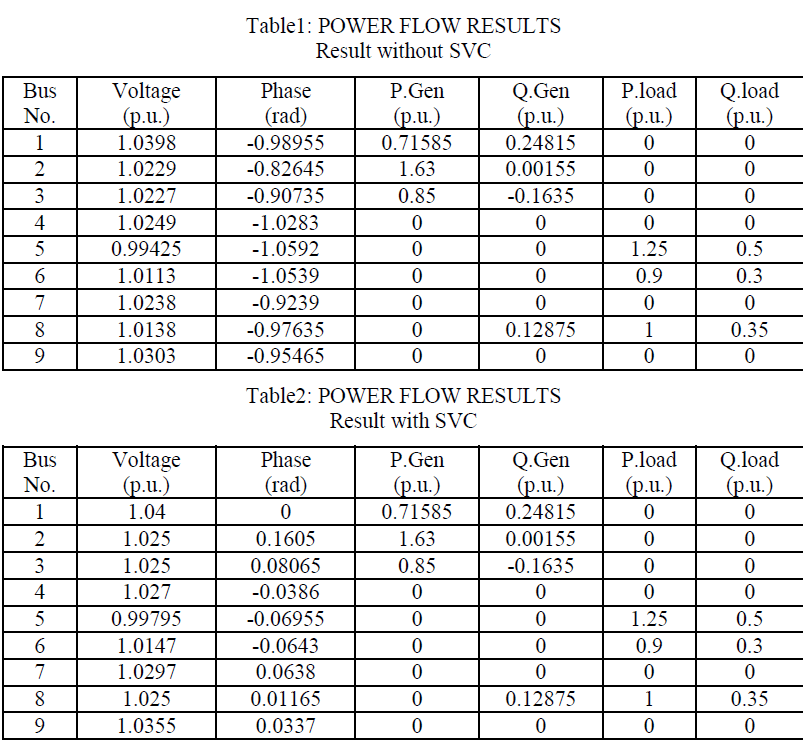 |
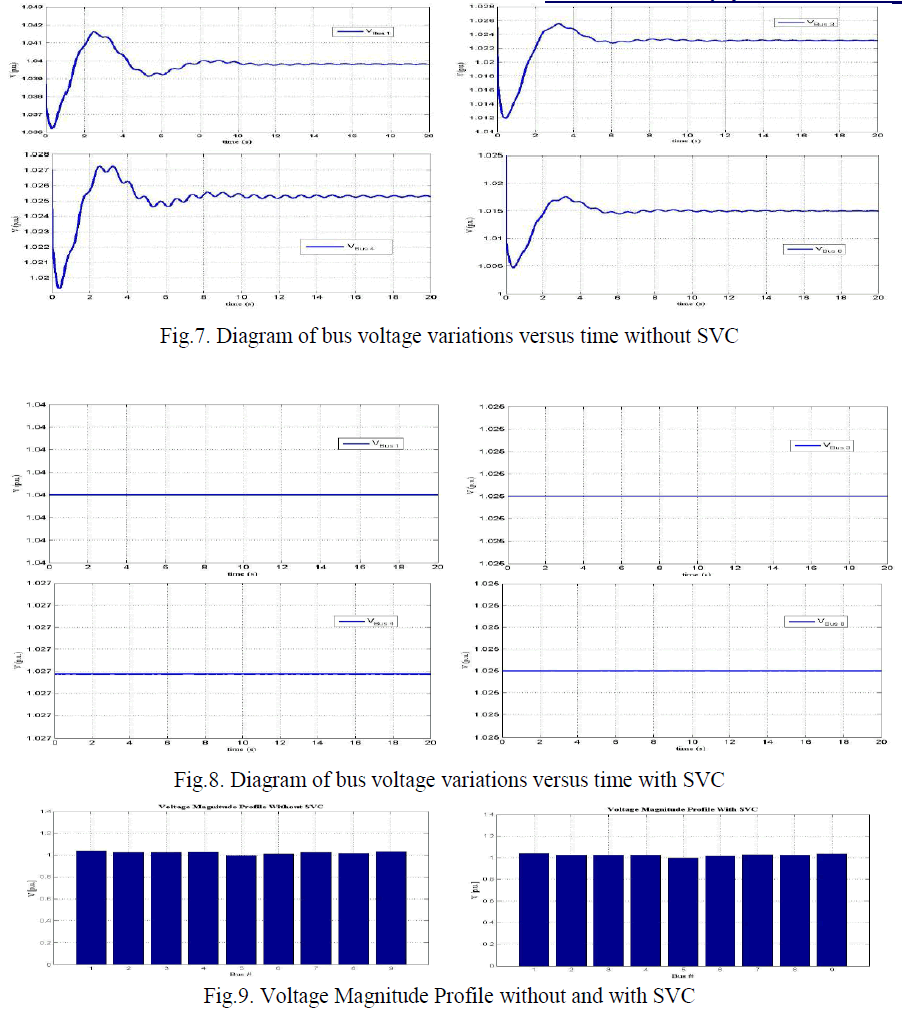 |
CONCLUSION |
| In this paper explores the effect of SVC on static voltage stability and presents the effect of Static VAR compensator (SVC) on Voltage Profile & Reactive Power for variable load conditions is investigated and presents static methods like Modal Analysis, Two Bus Thevenin Equivalent and Continuation Power Flow methods to predict the voltage collapse of the bus in the power system. WSCC 3-machine, 9-bus system has been used to demonstrate the ability of SVC in improving the voltage stability margin. SVC is main commercially available shunt FACTS controller for voltage control in power systems. The stability margin or the distance to voltage collapse is identified based on voltage and reactive power variation. Furthermore, the result can be used to evaluate the reactive power compensation and better operation & planning. The critical loading of the weak bus is determined by using Two Bus Equivalent method in a single shot rather than repetitive load flow solution of NR method and its critical loading is enhanced by placing the shunt compensation device called Static Var Compensator of different susceptance values. Continuation Power Flow method is used for determining the critical loading as well as the voltage profile of the test system with and without placement of SVC is observed. The reactive power support to the weak bus is provided by using shunt connected FACTS device Static Var Compensator (SVC) which is modeled as variable suscpetance mode. The voltage stability of the weak bus is enhanced after the placement of SVC. |
References |
|