ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Sridhar Chakravarthy D1, Md.Jani Pasha2, Dr. Himani3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper presents a methodology of modulation-based for generating pulse waveforms with selective harmonic elimination technique. In order to deal with harmonic elimination, a sine wave is compared with carrier triangular wave traditionally digital is presented. This approach requires a modified carrier waveform that can be calculated based on concise functions requiring only depth of modulation as input and does not require an initial guess while doing calculations for conventional offline solutions of switching angles and solution of coupled transcendental equations is not required. It also connects modulation to a harmonic elimination process
Keywords |
| Pulse width Modulations (PWM), Selective Harmonic Elimination (SHE), Fast Fourier Transform (FFT), Matlab (simulation). |
INTRODUCTION |
| Selective Harmonic Elimination (SHE) has been a research topic since the early 1960‘s, first examined in and developed into a mature form in during the 1970‘s is a long established method of generating pulse width modulation (PWM) with low baseband distortion [1]–[6]. Originally, it was useful mainly for inverters with naturally low switching frequency due to high power level or slow switching devices. Conventional sine-triangle PWM essentially eliminates baseband harmonics for frequency ratios of about 10:1 or greater [7], so it is arguable that SHE is unnecessary. However, recently Selective Harmonic Elimination (SHE) has received new attention for several reasons. Selective Harmonic Elimination (SHE) offers several advantages compared to traditional modulation methods including acceptable performance with low switching frequency to fundamental frequency ratios, direct control over output waveform harmonics, and the ability to leave triple harmonics uncontrolled to take advantage of circuit topology in three phase systems. First, digital implementation has become common. Second, it has been shown that there are many solutions to the selective harmonic elimination (she) problem that were previously unknown [8]. Each solution has different frequency content above the baseband, which provides options for flattening the high-frequency spectrum for noise suppression or optimizing efficiency. Third, some applications, despite the availability of high-speed switches, have low switching-to-fundamental ratios One ex-ample is high-speed motor drives, useful for reducing mass in applications like electric vehicles [9]. These key advantages make SHE a viable alternative to other methods of modulation in applications such as ground power units, dual-frequency induction heating. Selective harmonic elimination (she) is normally a two-step digital process. First, the switching angles are calculated offline, for several depths of modulation, by solving many nonlinear equations simultaneously. Second, these angles are stored in a look up table to be read in real time. Much prior work has focused on the first step because of its computational difficulty. One possibility is to replace the Fourier series formulation with another orthonormal set based on Walsh functions [10]–[12]. The resulting equations are more tractable due to the similarities between the rectangular Walsh function and the desired wave-form. Another orthonormal set approach based on block-pulse functions is presented in [13]. In [14][20], it is observed that the switching angles obtained traditionally can be represented as regular-sampled PWM where two phase-shifted modulating waves and a âÃâ¬Ãâ¢pulse position modulationâÃâ¬Ãâ technique achieve near-ideal elimination. Another approximate method is posed by [21] where mirror surplus harmonics are used. This involves solving multilevel elimination by considering reduced harmonic elimination waveforms in each switching level. In [22], a general-harmonic-families elimination concept simplifies a transcendental system to an algebraic functional problem by zeroing entire harmonic families. Faster and more complete methods have also been researched. In [23], an optimal PWM problem is solved by converting to a single unvaried polynomial using Newton identities, Padé approximation theory, and symmetric function properties, which can be solved with algorithms that scale as O . If a few solutions are desired, prediction of initial guess values allows rapid convergence of Newton iteration [24]. Genetic algorithms can be used to speed the solution [25], [26]. An approach that guarantees all solutions fit narrowly posed selective harmonic elimination (she) problem trans-forms to a multivariate polynomial system [27]–[30] through trigonometric identities [31] and solves with resultant polynomial theory. Another approach [32]–[34] that obtains all solutions to a narrowly-posed problem uses homology and continuation theory. Reference [35] points out the exponentially growing nature of the problem and proposes the âÃâ¬Ãâ¢simulated annealingâÃâ¬Ãâ method as a way to rapidly design the waveform for optimizing distortion and switching loss. Another optimization-based approach is given in [36] and [37], where harmonics are minimized through an objective function to obtain good overall harmonic performance. There have been several multilevel and approximate real-time methods proposed; these are beyond the scope here but discussed briefly in [38]. This manuscript proposes an alternative real-time selective harmonic elimination (SHE) method based on modulation. A modified triangle carrier is identified that is compared to an ordinary sine wave. In place of the conventional offline solution of switching angles, the process simplifies to generation and comparison of the carrier and sine modulation, which can be done in minimal time without convergence or precision concerns. The method does not require an initial guess. In contrast to other selective harmonic elimination (SHE) methods, the method does not restrict the switching frequency to an integer multiple of the fundamental. The underlying idea was proposed in [39] but has been refined here to identify specific carrier requirements that exactly eliminate harmonics and improve performance in deeper modulation. The method involves a function of modulation depth that is derived from simulation and curve fitting. In this respect, it has some similarity to [15] and [16], in which approximate switching angles are calculated and fitted to simple functions for cases of both low-( 0.8 p.u.) and high-modulation depth. It is interesting that the proposed approach connects modulation to a harmonic elimination process. Carrier waveform modulation, the proposed technique is not a variation of random-frequency carriers. Instead, the carrier waveform is modified in a specific and deterministic way to bring about a certain effect. The proposed method is readily implemented in real time. The switching signals themselves can be generated by analog comparison, while the modified carrier is generated with fast digital calculation and digital-to-analog conversion. |
SIGNAL DEFINITIONS AND SIMULATED RESULTS |
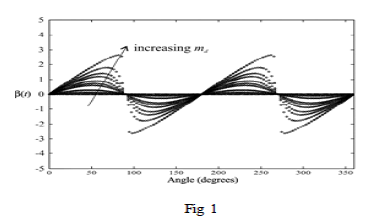
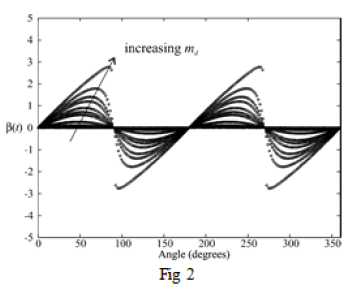
| Considering a quasi-triangular waveform to be used as the carrier signal in a PWM implementation. In principle, the frequency and phase can be modulated. To represent this, consider a triangular carrier function written as |
 |
 |
 |
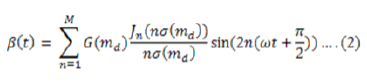 |
 |
 |
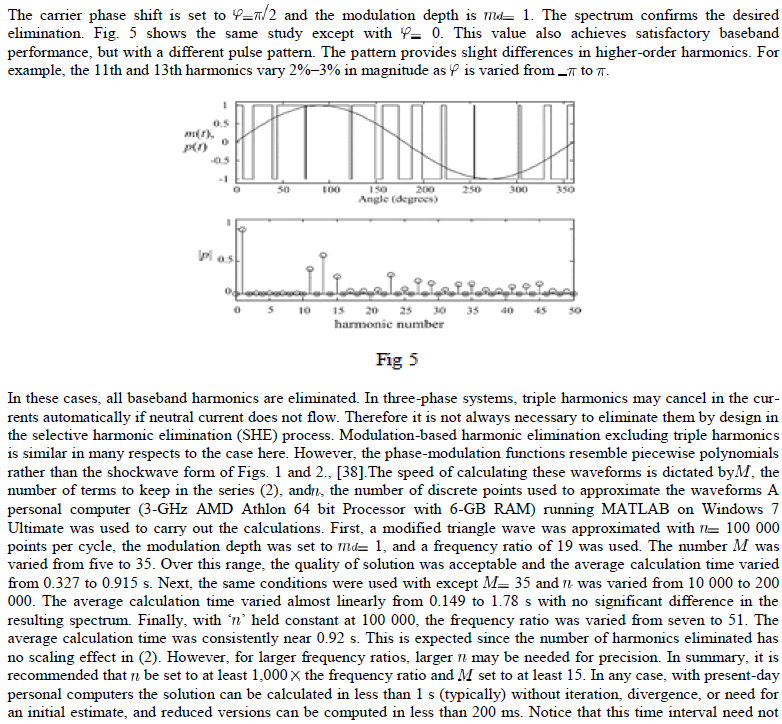 |
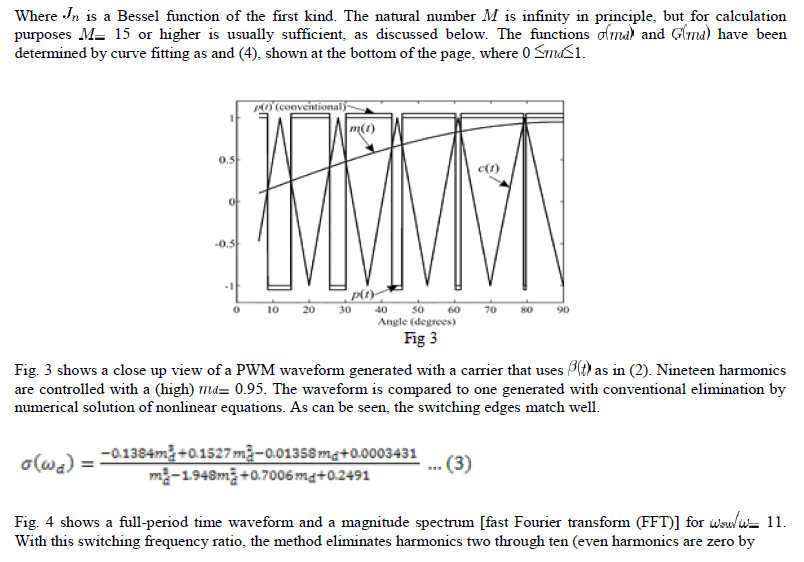
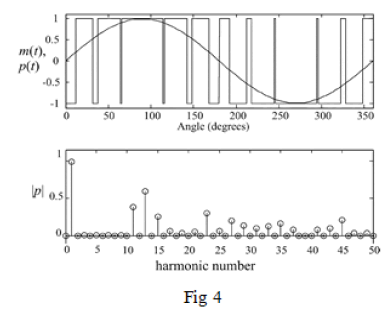
| cause trouble with real-time implementations. The carrier only needs to be recomputed with the modulation signal changes. In applications such as uninterruptible supplies, this is infrequent. In motor-drive applications, a response time of 200 ms to a command change may be acceptable as is. Alternatively, a look-up table can store some of the relevant terms to speed up the process dramatically. Dedicated DSP Please defines DSP algorithms will be much faster than PC computations based on MATLAB. |
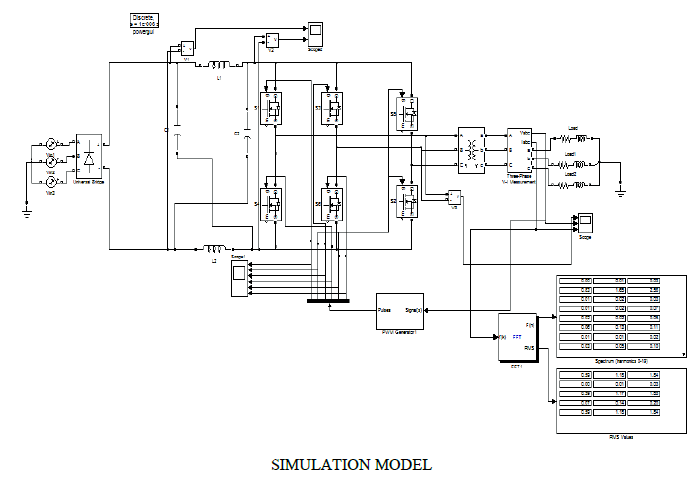 |
EXPERIMENTAL EXAMPLES |
 |
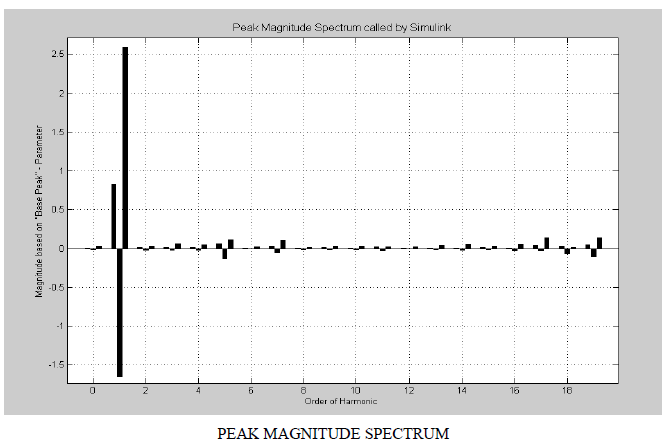 |
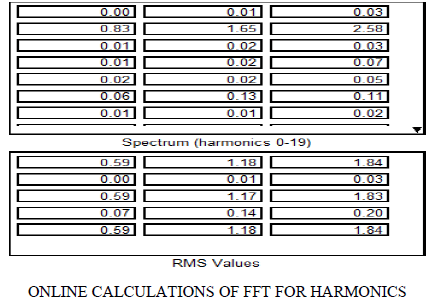 |
CONCLUSION |
| A method for calculating and implementing selective harmonic elimination (SHE) switching angles was proposed and by varying the periodicity of the carrier signal Modulation index improved. This improves THD. The method is based on modulation rather than solution of nonlinear equations. This approach is based on a modified carrier waveform which can be calculated based on concise functions requiring only depth of modulation as input. It rapidly calculates the desired switching waveforms while avoiding iteration and initial estimates. Calculation time is insensitive to the switching frequency ratio so elimination of many harmonics is straightforward. It is conceivable the technique could be realized with low-cost microcontrollers for real-time implementation. Once the carrier is computed, a conventional carrier-modulator comparison process produces switching instants in real time. |
References |
|