ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Narottam dutt upadhyay1, Rameshwar singh2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
This paper presents a biogeography-based optimization (BBO) algorithm to solve both convex and nonconvex economic load dispatch (ELD) problems of thermal plants. Lack of exploration capability of biogeographybased optimization (BBO) leads to slow convergence. The proposed methodology can take care of economic dispatch problems involving constraints such as transmission losses, valve point loading, multi-fuel options and prohibited operating zones. Biogeography is the study of the geographical distribution of biological organisms. Mathematical equations that govern the distribution of organisms were first discovered and developed during the 1960s. The mindset of the engineer is that we can learn from nature. This motivates the application of biogeography to optimization problems; the BBO is based on two steps mutation and migration. The purpose of this work is to find out the advantages of application of the soft computing technique and BBO in particular to the economic load dispatch problem.
Keywords |
| Biogeography-Based Optimization (BBO), Economic Load Dispatch (ELD), Valve-Point Effect, PSO.. |
I. INTRODUCTION |
| Achieve the benefits of minimum production cost, better operating conditions and maximum reliability is the basic object of the electrical systems. The economic load is the process of on-line allocation of generating units, wherein it is required to distribute the load among the generating units, in such a way as to minimize the total operating cost of generating units and satisfying system equality and inequality constraints. Since the load demands swings continuously hence it is very difficult to satisfy the demands in the minimum cost [1]. The fuel cost curve characteristic is nonlinear due to presence of various equality and inequality constraints, Economic load dispatch (ELD) seeks âÃâ¬Ãâ¢the bestâÃâ¬Ãâ generation schedule for the generating plants to supply the required demand plus transmission losses at minimum production cost. Various investigations on ELD have been undertaken until date, as better solutions would result in significant economical benefits. Previously a number of derivative-based approaches including Lagrangian multiplier method have been applied to solve ELD problems [2]. Over the past few decades, as an alternative to the conventional mathematical approaches, many salient methods have been developed for ELD problem such as evolutionary programming [3], particle swarm optimization [4], Genetic algorithm [5], and improved tabu search [6]. Recently a new population based evolutionary algorithm has been invented by Simon, based on biogeography. This has better properties than other evolutionary algorithms hence can be employing in power system optimization problems. Biogeography is way of natural for species distribution on the earth. In BBO algorithm, a good solution for a problem considered as a habitat with high HSI and a poor solution considered as a habitat with low HSI. A good solution tends resist to any changes but a poor solution has a tendency to copy good properties from a good solution. Good properties remain in the high HSI habitat and at the same time appear in low HSI habitats as a new feature. This accepting of good features from good solutions may help the low HSI habitats to be a high HSI habitat. The BBO algorithm has some advantages in comparison to other algorithms. In BBO and PSO each solution stay survive to the end of optimization procedure but in most of evolutionary based algorithms, solutions die at the end of each generation. In some of evolutionary due to crossover step, good solutions lose their efficiency but in BBO do not have crossover step [7].In this paper a newly developed Biogeography based optimization (BBO) algorithm has been applied to the ELD problems. The BBO algorithm was developed by D. Simon in the year 2008 from the theory of Biogeography as its base [8].To show the effectiveness of the BBO, the BBO algorithm has been applied to without Valve-Point Effects and with Valve-Point Effects and comprising of three generating units .The results of BBO are compared with the PSO and its variants method and it has been found that the BBO algorithm shows superior performance. |
II. ECONOMIC LOAD DISPATCH (ELD) |
| The objective of an ELD problem is to find the optimal combination of power generations that minimizes the total generation cost while satisfying equality and inequality constraints [9]. The fuel cost curve for any unit is assumed to be approximated by segments of quadratic functions of the active power output of the generator. For a given power system network, the problem may be described as optimization (minimization) of total fuel cost as defined by (1) under a set of operating constraints. |
| A. ELD Problem without Valve-Point Effects |
| Where is FT total fuel cost of generation in the system ($/hr), ai, bi, and ci are the cost coefficient of the i th generator, Pi is the power generated by the i th unit and n is the number of generators. |
| The objective of ELD is to minimize the overall cost of generation. Power balance constraint The total generation cost is minimized subjected to the following constraints Power balance constraint |
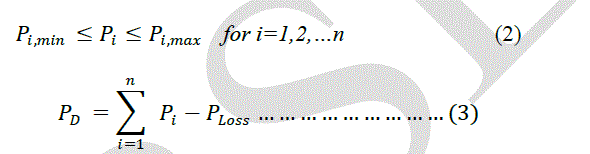 |
| where Bij is coefficient of transmission losses. |
| B. ELD Problem Considering Valve-Point Effects |
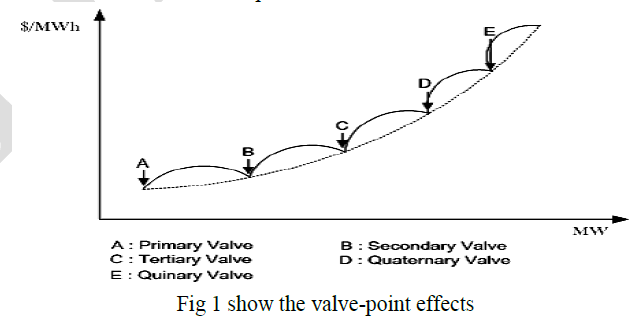
| The generating units with multi-valve steam turbines exhibit a greater variation in the fuel-cost functions [15]. The valve opening process of multi-valve steam turbines produces a ripple-like effect in the heat rate curve of the generators. These âÃâ¬Ãâ¢valve-point effects are illustrated in Fig. 1. The significance of this effect is that the actual cost curve function of a large steam plant is not continuous but more important it is non-linear. |
 |
| The valve-point effects are taken into consideration in the ELD problem by superimposing the basic quadratic fuelcost characteristics with the rectified sinusoid component as follows: |
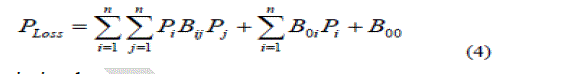 |
III. OVERVIEW OF BIOGEOGRAPHY-BASED OPTIMIZATION ALGORITHM (BBO) TECHNIQUE |
| The Biogeography-based optimization algorithm [12] has been developed from the theory of Biogeography as its base. Biogeography is the study of the geographical distribution of biological organisms. Mathematical models of biogeography describe how the biological organisms or species, to be more specific, migrate from one island to another, how new species arise, and how these species become extinct. An island can be defined as any habitat that is geographically isolated from other habitats. The concept of BBO is based on the migration and mutation operations. The concept and mathematical formulation of the migration and mutation operations are briefed below: |
| A. Migration |
| In BBO, the migration operation refers to the process of either entering or leaving of the species into or from an island. Like PSO and other population based search techniques, BBO also uses a population of candidate solutions for optimization purpose. Representation of each candidate solution is done as a vector of real numbers. Here each real number in the population is considered as one suitability index variable (SIV). In ED problem, these SIVs are analogous to the power output of the generators. The SIVs in one array are used to calculate the habitat suitability index (HSI) of a habitat. The HSI is analogous to the objective function as used in other techniques. In ED problem, the HSI is analogous to the generation cost of a generator. Solutions with high HSI represent a superior solution whereas solutions with low HSI represent an inferior solution. The process of species entering a habitat is known as immigration whereas the process of leaving a habitat is known as emigration. The immigration rate, λ and the emigration rate, μ of each habitat is used to probabilistically share information with other habitats/solutions. Each solution is modified according to probability ïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿý, known as the habitat modification probability, based on other solutions. If a particular habitat is selected for modification, then its λ is used to probabilistically decide whether or not to modify each SIV of that habitat. If a particular SIV in a given habitat is selected for modification, then μ of other habitats are used to probabilistically decide which of the habitats should migrate a randomly selected SIV from those habitats to that particular habitat. Unlike other AI techniques where the recombination process is used to generate a completely new solution, the migration operation in BBO is used to bring changes within an existing solution. In order to prevent the best solutions from being changed by the migration process, few elite solutions are kept the same in the consequent iterations. Immigration and emigration rate for habitat containing ïÿýïÿý species is given as |
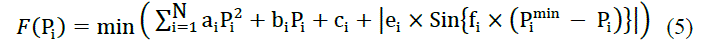 |
| I, E: the maximum immigration and emigration rates respectively |
| N: maximum number of species that a habitat can contain |
| B. Mutation |
| If some disastrous events happen, the HSI of a habitat can change drastically resulting in the species count to differ from its equilibrium value. In BBO this process is modeled as SIV mutation and the mutation rates of the habitats can be calculated using the species count probabilities given below Sudden changes in climate of one habitat or other incidents will cause the sudden changes in HSI of that habitat. In BBO algorithm, this situation can be model in the form of sudden changes in value of SIV. The probability of any organism can be calculated by the following equation. |
 |
| Each member of one habitat has its own probability. If this probability is too low, then this solution has high chance to mutate. In the same manner, if probability of a solution is high that solution has a little chance to mutate. Consequently, solutions with high HSI and low HSI have a little chance to development a better SIV in the next iteration. Unlike high HSI and low HSI solutions, medium HSI solutions have a greater chance to development better solutions after mutation procedure. |
| In the following equation mutation rate of each solution can be calculated. |
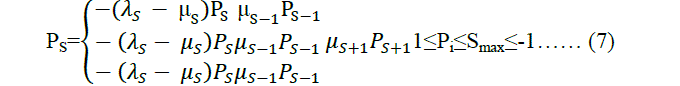 |
| Where, |
| m(s) : the mutation rate for habitat containing exactly s species |
| ïÿýïÿýmaxâÃÂá : Largest of all the ïÿýïÿýs values |
| This kind of mutation is inclined to increase diversity between solutions. At this stage, there is also a elitism to prevent the answers from getting worse after mutation procedure. In this case, if a SIV is selected for mutation operation, one authorized random number is substituted. |
| C. Biogeography based Economic load dispatch algorithm |
| A new approach to implement the BBO algorithm will be described for solving the ELD problem. Especially, suggestion will be given on how to deal with the equality and inequality constraints of the ELD problems when modifying each individual’s search point in the BBO algorithm. The process of BBO algorithm can be explained as follows [8]- [11]. |
| Step 1: Initialization of BBO parameters: Choose the number of generators i.e. number of SIVs, number of habitats i.e. population size, power demand, loss coefficients, habitat modification probability ïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿý = 1, mutation probability = 0.1, maximum mutation rate ïÿýïÿýïÿýïÿýïÿýïÿýïÿýïÿý, maximum immigration rate I = 1, maximum emigration rate E = 1, step size for numerical integration dt = 1, elitism parameter = 2. |
| Step 2: Initialization of SIVs: Each SIV of a habitat is initialized randomly while satisfying the constraints of (3). Each habitat represents a potential solution to the given problem. |
| Step 3: Calculation of HSIs: HSI for each habitat is calculated for given immigration and emigration rates. HSI represents the fuel cost of the generators. |
| Step 4: Identification of elite habitats: Based on the HSI values, elite habitats are identified i.e. those habitats for which the fuel cost is minimum, are selected. |
| Step 5: Performing migration operation: For each of the non-elite habitats, migration operation is performed. HSI for each habitat is recomputed. SIVs obtained after migration must satisfy the constraints of (3). |
| Step 6: Performing mutation operation: Species count probability of each habitat is updated using (7). Mutation operation is carried out on the non-elite habitats. HSI value of each new habitat set is recomputed. |
| Step 7: Stopping criterion: Go to step 3 for next iteration. If the predefined number of iterations is reached, stop the process. |
IV.RESULTS AND ANALYSIS |
| The applicability and validity of the BBO algorithm for practical applications has been tested on various test cases. All the programs are developed using MATLAB 7.01 and the system configuration is Pentium IV processor with 3.2 GHz speed and 1 GB RAM |
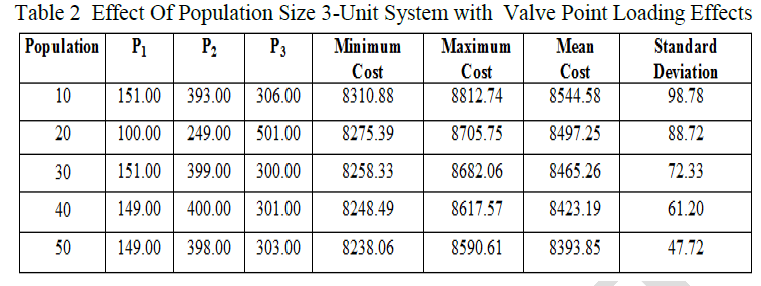
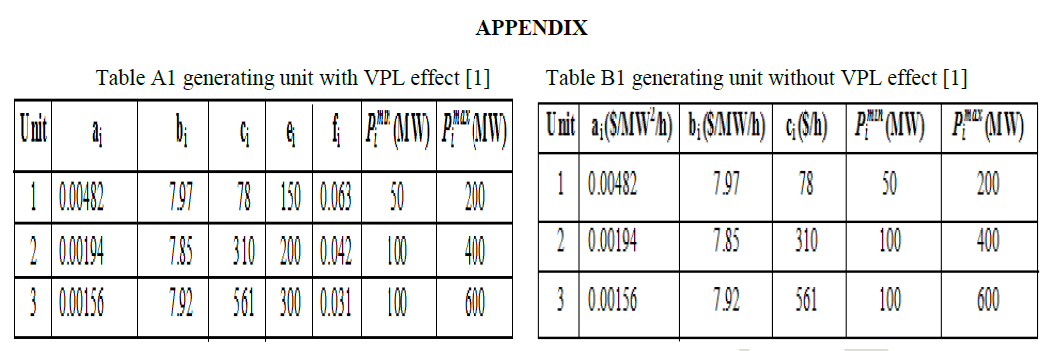
| Case A - Effect of Population Size In 3-Generating Units with Valve Point Loading Effects |
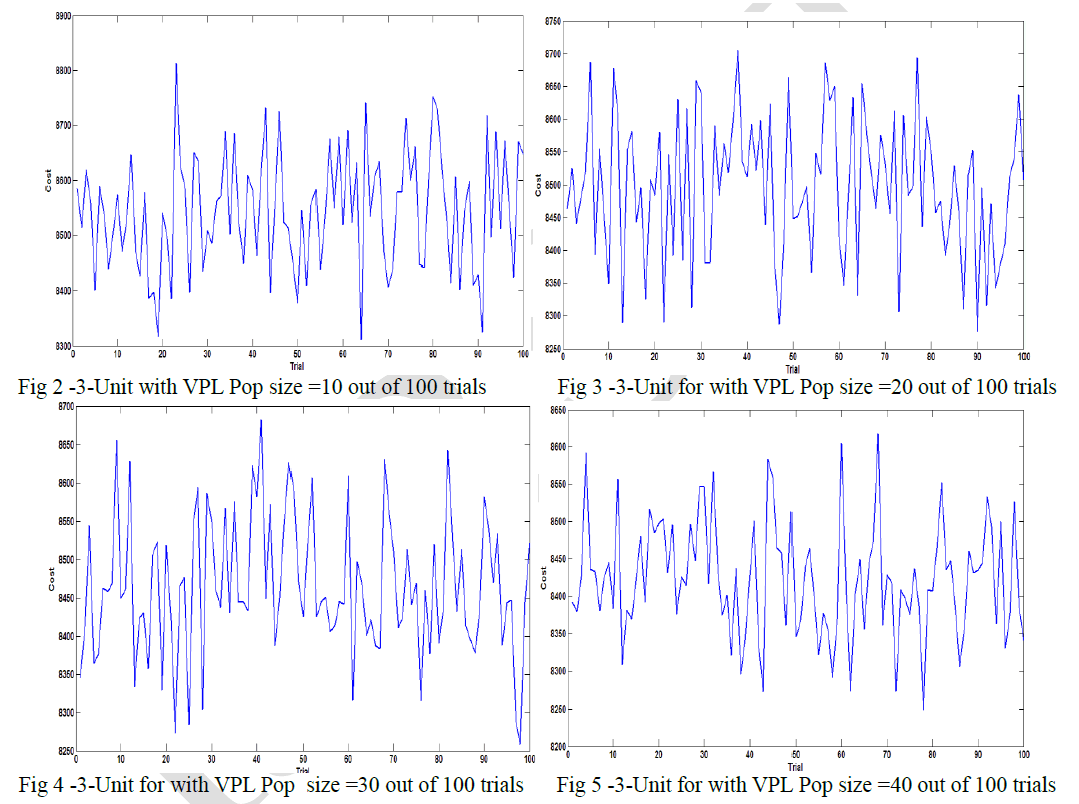
| The cost coefficients and other data of the three generating unit system is listed in Table A1 in the appendix section the load demand is 850 MW. Their best results are shown in Table 2 that the minimum, mean, maximum, and standard deviation of the population out of 100 trials goes on improving with increase in population. It can be observed that the population size= 10,20,30 and 40 are show in the figure 2,fig 3,fig 4 and fig 5 for best parameters for this case after 100 Trials, which is very close to global minima. |
 |
 |
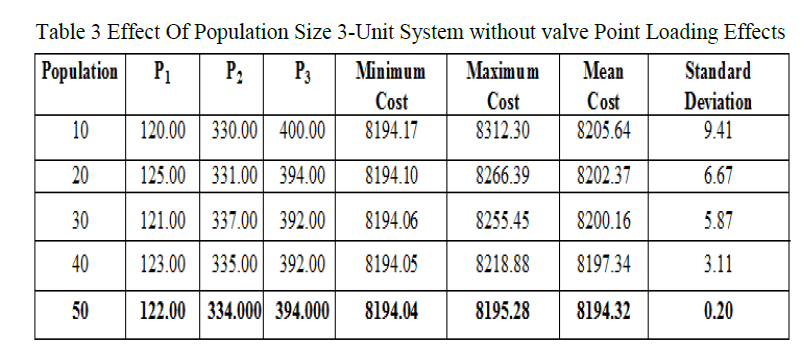
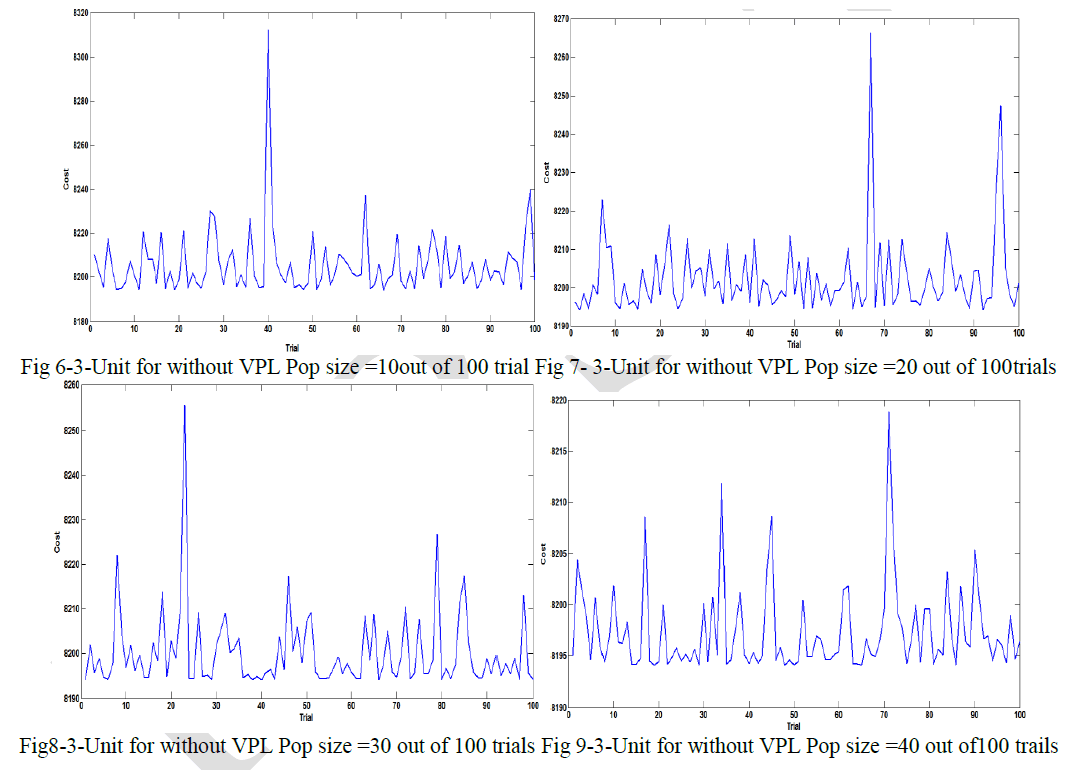
| Case B Effect of Population Size in 3-Generating Units without valve Point Loading Effects |
| The cost coefficients and other data of the three generating unit system is listed in Table B1 in the appendix section. BBO achieved quite effective result. A parameter tuning was done to find optimal values of M.R. 05 and Population 10, 20, 30, 40 and 50 sizes for the practical ELD problem using BBO. It can be observed from Table 3. Show the Fig 6 ,Fig7,Fig 8 ,the convergence characteristics of the 3-generating units with VPL. |
 |
 |
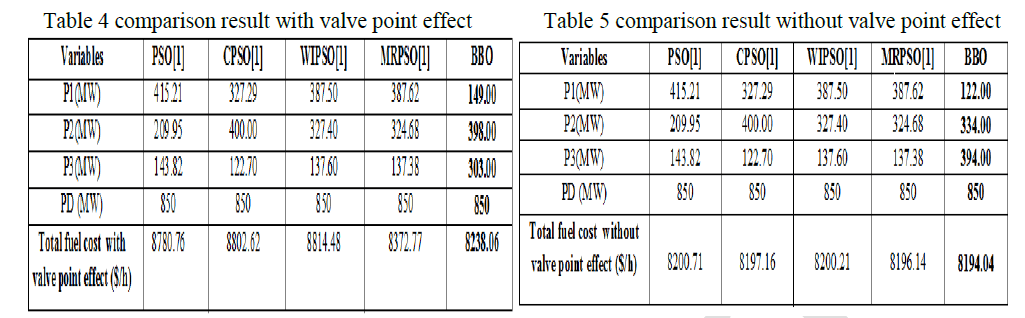
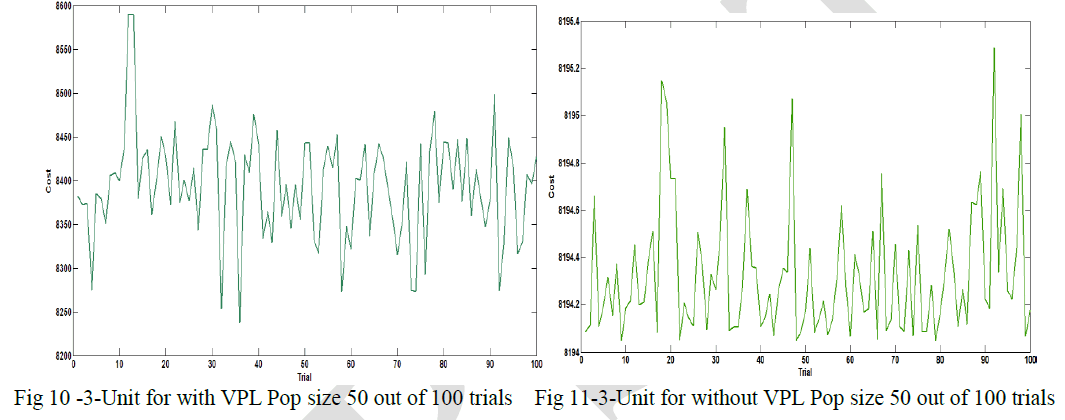
| Case –C Comparison of Results for 3 unit system |
| BBO achieved quite effective result. A parameter tuning was done to find optimal values of M.R. 0.5 and Population sizes 50 out of 100 trials for with & without valve Point Loading Effects practical ELD problem , Results obtained from proposed BBO algorithm have been compared with PSO,CPSO,WIPSO and MRPSO [1],with and with valve Point Loading Effects. Comparison The best results of all evolutionary methods are shown in Table 4 & Table 5. And fig 10 and fig 11 that the proposed BBO algorithm provided better results compared to other reported evolutionary techniques. |
 |
 |
IV. CONCLUSION |
| In this paper, the biogeography-based optimization (BBO) algorithm has been applied to Economic Dispatch Problems (ELD) problems; Economic load dispatch is a challenging task in power system. ELD model characteristic should be nonlinear due to presence of valve point loading effect and presence of various constraints, the performance of this algorithm has been compared with PSO algorithm by employing different cases in 3 unit systems. The biogeographybased optimization (BBO) algorithm has the ability to find the better quality solution and has better convergence characteristics and computational efficiency. It is clear from the results obtained by different trials that the proposed BBO method has good convergence property and can avoid the shortcoming of premature convergence of other optimization techniques to obtain better quality solution, so Soft computing techniques like the BBO use random operators for achieving the optimal result therefore in every fresh trial, these methods converge to different solutions near the global best solution. |
 |
References |
|