ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Dr G. Sreenivasan1, B. Dheeraj Merin Babu2, K. Srikanth3, B. Rajesh Kiran4
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This project presents a novel and improved method for solving the Non Convex Economic Dispatch (ELD) problems with valve-point effects and Multiple Fuels, by integrating the particle swarm optimization (PSO) with the chaotic sequences and Cross over Operations. The results of the IPSO were compared with previous methods and the conventional Genetic Algorithm (GA), revealing that the results clearly show that the proposed IPSO outperforms other state-of-the-art algorithms in solving ELD problems with the valve-point effect.
Keywords |
| Chaotic sequence, constraint treatment technique, crossover operation, economic load dispatch problem, improved particle swarm optimization, non-convex optimization, multiple fuels, valve - point effects. |
Nomenclature |
 |
 |
INTRODUCTION |
| Many Power system optimization problems including economic dispatch (ELD) have non-convex characteristics with heavy equality and inequality constraints. The objective of ELD is to determine an optimal combination of power output to meet the demand at minimum cost while satisfying the constraints. For simplicity, the cost function for each unit in the ELD problems has been approximately represented by a single quadratic function and is solved using mathematical programming techniques. Generally, these mathematical methods require the derivative information of the cost function. Unfortunately, the input-output characteristics of generating units are non convex due to prohibited operating zones, valve-point loadings, Multi-fuel effects. Moreover, many generating units, particularly those which are supplied with Multi – fuel sources (Coal, Nature Gas or Oil) lead to the problem of determining the most economical fuel to burn. Thus, the practical ELD problem should be represented as a non convex optimization problem with constraints, which makes the challenge of finding the global optimum hard and, and it cannot be directly solved by mathematical methods. |
| Over the past decade, many salient methods have been developed to solve these problems, such as the Hierarchical Numerical method, Genetic Algorithm (GA), Evolutionary Programming, Tabu search, Neural Network Approaches, Differential Evolution, Particle Swarm Optimization (PSO), and Hybrid Artificial Intelligence (AI) method. However, few approaches for the ELD problem, and none of the studies mentioned above, consider both valve-point loadings and multi-fuel effects, which always exist in real power systems simultaneously. To obtain an accurate and practical Economic Dispatch solution, the realistic operation of the ELD problem should be taken both valve-point effects and multiple fuels into account. |
| The main advantages of the PSO algorithm are: simple concept, easy implementation, relative robustness to control parameters, and computational efficiency. Although the PSO-based approaches have several advantages, it may get trapped in a local minimum when handling heavily constrained problems due to the limited local/global searching capabilities. |
| The existing drawbacks of PSO to some extents, this paper propose an improved PSO (IPSO) framework combining the chaotic sequences and the crossover operation. The employment of chaotic sequences and the crossover operation in PSO can improve the global searching capability by preventing premature convergence through increased diversity of the population. In addition, an effective constraint handling technique is proposed to improve the solution quality without scarifying the computational efficiency. The suggested IPSO is applied to a non convex ELD problem consisting of 10untis-Generator system. The solutions are compared with those of state-of-the-art AI methods. |
FORMULATION OF ECONOMIC LOAD DISPATCH PROBLEM |
| Economic load dispatch problem assumes that there are N units already connected to the system. The purpose of economic load dispatch problem is to find the optimum operating policy for these N units. |
A. Objective function: |
| The minimization of simplified cost function of each generating unit can be represented as described as |
B. System constraints: |
| In case of economic load dispatch the generations are not fixed but they are allowed to take values again within certain limits so as to meet a particular load demand with minimum fuel consumption. The total cost of generation is function of the individual generation of the sources, which can take values within certain constraints; the cost generation will depend upon the system constraint for a particular load demand. This means the cost of generation is not fixed for a particular load demand but depends upon the system constraints of the sources. |
C. Equality constraints: |
| While minimizing the total generation cost, the total generation should be equal to the total system demand plus the transmission network loss. However, the network loss is not considered in this paper for simplicity. This gives the equality constraint. |
D. Inequality constraints: |
| The generation output of each unit should be between its minimum and maximum limits. That is, the following inequality constraint for each generator should be satisfied. |
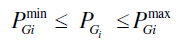 |
E. ELD problem with General smooth cost function: |
| The input-output characteristic of a steam unit is in idealized form as shown. The input to the unit shown on the ordinate may be either in terms of heat energy requirements [millions of Btu per hour (MBtu/h)] or in terms of total cost per hour ($ per Mwh). The output is normally the net electrical output of the unit. The characteristic shown in idealized, in that it is presented as smooth, convex curve. |
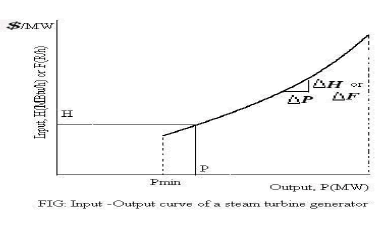 |
| The figure above in the case indicates the smooth cost function. The cost equation for above smooth curve can be written as |
| The solution of this function can be obtained by General ELD problem method. |
F. ELD problem with non – smooth cost functions: |
| In reality, the objective function of an ELD problem has non differentiable points according to valve – point effects and change of fuels; therefore the objective function should be composed of a set of non – smooth cost functions. In this project, two cases of non-smooth cost functions are considered. One is the case with the valve-point loading problem and the other is the case with the multiple fuel problems. |
G. Considering Valve-point Effects: |
| Large steam turbine generators will have a number of steam admission valves that are opened in sequence to obtain ever-increasing output of the unit. As the unit loading increases, there by the input to the unit increases and the incremental heat rate decreases between the opening points for any two valves. However, when a valve is first opened, the throttling losses increase rapidly and the incremental heat rate rises suddenly. This gives rise to the discontinuous type of characteristics in order to schedule steam unit, although it is usually not done. It is possible to use this type of characteristic in order to schedule steam units. This type of input – output characteristics is nonconvex; hence, optimization technique that requires convex characteristics may not be used with impunity. |
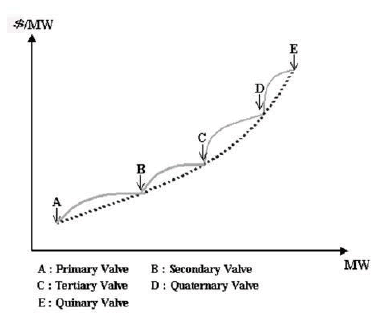 |
| In valve point loading problem the objective function is generally described as superposition of sinusoidal functions and quadratic function shown in equation. |
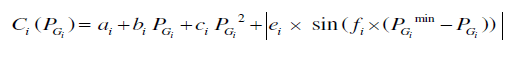 |
H. Considering Multi Fuels effect: |
| Any given unit with multiple cost curves needs to operate on the lower contour of the intersecting curves. The resulting cost function is called a “hybrid cost function.” Each segment of the hybrid cost function implies some information about the fuel being burned or the unit’s operation. Since the dispatching units are practically supplied with multi-fuel sources, each unit should be represented with several piecewise quadratic functions reflecting the effects of fuel type changes, and the generator must identify the most economic fuel to burn. Thus, the fuel cost function should be practically expressed as Thus the fuel Cost Function should be practically expressed as |
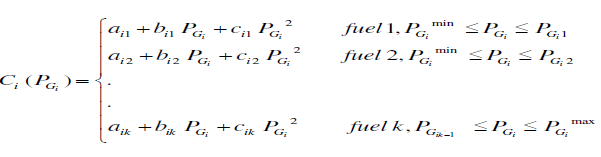 |
I. Considering both Valve-point Effects and Multi Fuels effect: |
| To obtain an accurate and practical economic dispatch solution, the realistic operation of the ELD problem should be considered both valve-point effects and multiple fuels. This project proposed an incorporated cost model, which combines the valve-point loadings and the fuel changes into one frame. Therefore, the cost function should combine (5) with (6), and can be realistically represented as shown in (10), as below |
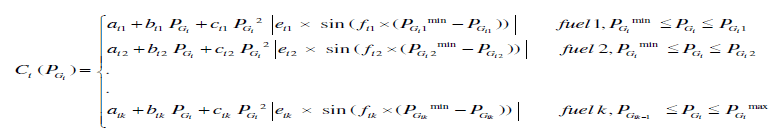 |
OVER VIEW OF THE PSO |
| Particle swarm optimization (PSO) based on the analogy of swarm of bird. PSO applies the concept of social interaction to problem solving. It uses a number of agents (particles) that constitute a swarm moving around in the search space looking for the best solution. Each individual makes his decision using own experience together with other individuals’ experiences, each particle keeps track of its coordinates in the solution space which are associated with the best solution (fitness) that has achieved so far by that particle. This value is called personal best, Pbest. Another best value that is tracked by the PSO is the best value obtained so far by any particle in the neighbourhood of that particle. This value is called Gbest. |
| The basic concept of PSO lies in accelerating each particle towards its Pbest and the Gbest locations, with a random weighted acceleration at each time step. |
| The PSO algorithm searches in parallel using a group of individuals similar to other AI-based heuristic optimization techniques. Each individual corresponds to a candidate solution to the problem. Individuals in a swarm approach to the optimum through its present velocity, previous experience, and the experience of its neighbours. In a physical n-dimensional search space, the position and velocity of individual ‘i’ are represented as the vectors |
 |
A. Application of chaotic sequences in PSO: |
| Chaos, apparently disordered behavior that is nonetheless deterministic, is a universal phenomenon that occurs in many areas of science. Coelho and Mariani combined the chaotic sequences with the mutation factor in differential evolution to improve the solution quality. Caponetto et al. applied various chaotic sequences in evolutionary algorithms (EAs) in lieu of the random numbers. Shengsong et al adopted a chaotic hybrid algorithm to solve the optimal power flow problems. The application of the chaotic sequences has shown promising results in some engineering applications. |
| One of the dynamic systems evidencing chaotic behavior is the iterator called the logistic map, whose equation is described as follows: |
| Despite the apparent simplicity of the equation, the solution exhibits a rich variety of behaviors. The behavior of the system represented by is greatly changed with the variation of μ. The value of μ determines whether f stabilizes at a constant size, oscillates between limited sequences of sizes, or behaves chaotically in an unpredictable pattern. And also the behavior of the system is deterministic, displaying chaotic dynamics when μ = 4.0 and f0 ∉ {0, 0.25, 0.50, 0.75 1.0}. |
| The performance of a PSO can depend on its parameters such as the inertia weight factors and two acceleration coefficients. The first term in (13) represents the influence of previous velocity, which provides the necessary momentum for particles to fly around in a search space. The balance between exploration and exploitation can be treated by the value of inertia weight. |
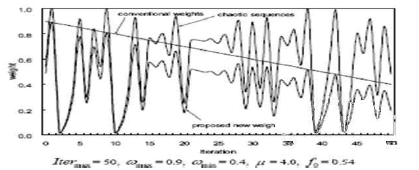 |
| Therefore, a proper control of inertia weight is very important to find the optimum solution efficiently. Shi and Eberhart made a significant improvement in the performance of the PSO with a linearly varying inertia weights over the iterations, which is widely used in PSO applications. In this Project, in order to improve the global searching capability and to increase the probability of escaping from a local minimum, a new weight-changing approach, Chaotic Inertial Weight Approach (CIWA), is suggested as defined as follows: |
| Whereas the weight in the conventional IWA decreases monotonously from max to min the proposed chaotic weight decreases and oscillates simultaneously as shown in Fig. 1. Since the suggested CIWA can encompass the whole weight domain under the decreasing line in a chaotic manner, the searching capability of the proposed algorithm can be increased as illustrated in numerical studies. |
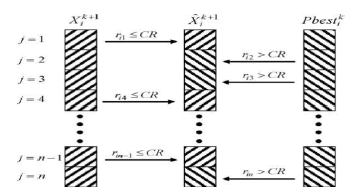
B. Crossover operation: |
 |
 |
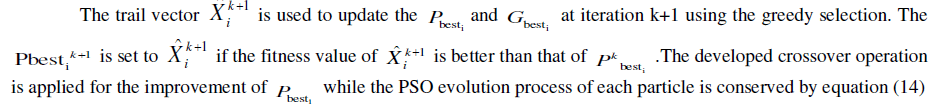 |
TREATMENT OF EQUALITY AND INEQUALITY CONSTRAINTS |
| It is very important to create a group of particles satisfying the equality and inequality constraints. The summation of all elements within a particle should be equal to the total system demand and each element j in particle i should be within its operating boundaries. Therefore, it is necessary to develop a strategy for satisfying the constraints. This project proposes an efficient heuristic constraint – handling technique as follows |
 |
IMPLEMENTATION OF IMPROVED PSO ALGORITHM FOR ELD PROBLEMS |
 |
| Step 1: Initialize the position and velocity of a population at random while satisfying the constraints. |
| Step 2: Update the velocity of particles. |
| Step 3: Modify the position of particles to satisfy the constraints, if necessary. |
| Step 4: Generate the trail vector through crossover operation process. |
| Step 6: Go to Step 2 until stopping criteria is satisfied. |
| In the following, the detailed implementation strategies of the proposed method are described. |
A. Creating initial position and velocity: |
| In the initialization process, a set of particles is created at random as follows: |
| Where ij r is a uniformly distributed random number between [0, 1]. Here, the minimum and maximum power outputs should be adjusted when the ramp rate limits are considered. Although each element satisfies the inequality constraint, the problem of equality constraint still remains to be resolved. To do this, the aforementioned equality constraint treatment strategy is applied. After creating the initial position of each particle, the velocity of each particle is also created at random. |
B. Movement of the particles: |
| To modify the position of each particle, it is necessary to calculate the velocity of each particle in the next stage by (13).In this process, the new weight approach CIWA of (17) is employed to improve the global searching capability. After that, the position of each particle is updated by (14). Since the resulting position of a particle is not always guaranteed to satisfy the constraints, the constraint treatment procedure is performed. |
C. Crossover operation: |
 |
E. Stopping criteria: |
| The proposed IPSO algorithm is terminated if the iteration reaches a pre-defined maximum iteration. |
TEST SYSTEMS AND RESULTS |
A. TEST SYSTEM: 10 units generating system with Valve-point Effects and Multi Fuels Effect |
| Few attempts have been made at considering both valve-point effects and multiple fuels for the realistic ELD problem. The complete solution procedure for the problem stated has been explained by taking an example of 10 generating units considering both multi-fuels and valve-point effects. The input data and related constraints of the test system are given in [6]. |
| The total system demand is set to 2700 MW. The values for c1, c2, and CR are set to be 2.0, 2.0, and 0.2, respectively, Number of particles = 40, Inertia weight parameters Wmax =0.9, Wmin=0.4, Control Parameter of chaotic Sequences U=4.0, Initial valve of f is random number between [0 1] expect for 0, 0.25, 0.5, 0.75 and 1. |
 |
| To meet the total load demand PD, each generating unit (out of ten units) has to generate power such that the total generating cost is minimum. |
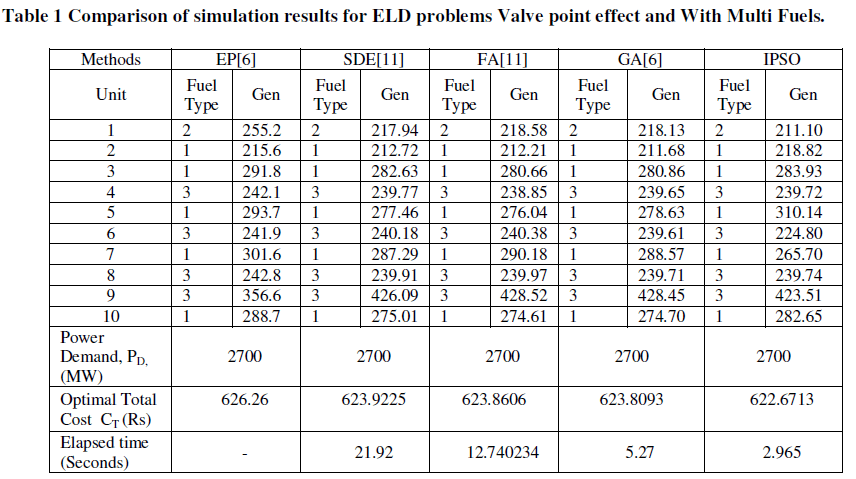
| The iterative Procedure is adopted for solution. The solution was tried for iterations up to 200. A function program is developed using MATLAB 7.0.1 software to compare the generation cost of each unit depending on the fuel used. The optimum power generations of generating units and their fuel types, the best fuel cost values are given in Table-1, below. The convergence characteristics of IPSO algorithm for solving the problem with the consideration of these two effects is show in fig - 1 |
| The operating cost of fuel is this case is 622.671 $ which is very less when compared to other existing methods. The solution is converged in 2.965 seconds which is comparatively very less with respect to other existing methods |
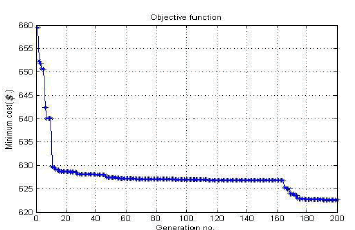 |
| Fig - 1 Convergence characteristics of IPSO algorithm for 10-unit system considering Both Valve Point Effects and Multi Fuels |
CONCLUSIONS |
| Few reports have been made at units considering both valve-point effects and multiple fuels for the realistic ELD problem, which always exist in real power systems simultaneously. This paper proposes the IPSO technique to solve the practical ELD operation. The realistic ELD problem is complicated because both valve-point loadings and change fuels must be considered. The IPSO helps the proposed algorithm to efficiently search and actively explore the solution, and efficaciously handle constraints of the system. |
| The proposed IPSO employs the chaotic sequences as well as the crossover operation to enhance the performance of the conventional PSO. The chaotic sequences combined with the linearly decreasing inertia weights are devised to improve the global searching capability and escape from a local minimum. In addition, the crossover operation is introduced to increase the diversity of the population. These strategies not only improve the global searching ability but also prevent the solution from trapping in a local optimum point. In addition, a more efficient constraint treatment strategy is proposed. The proposed IPSO algorithms have been successfully applied to ELD problems of 10 Unit – Generating system. The proposed IPSO have found better solutions than the other existing methods so far. The results clearly show that the proposed IPSO framework can be used as an efficient optimizer providing satisfactory solutions for general non convex ELD problems; |
ACKNOWLEDGEMENT |
| The authors greatly acknowledge the Directors, Principal and Staff of Electrical and Electronics Engineering Department, Intell Engineering College, Intell campus, Anantapuramu, Andhra Pradesh, India for their continuous support encouragement and the extensive facilities provided to carry out this work. |
References |
|