ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
R. Helen1, R.Sumathi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
The objective of this paper is to find the single machine scheduling problem of n-jobs which minimizes the sum of the total tardiness of each job using dynamic programming method by type-2 trapezoidal fuzzy numbers. The effectiveness of the proposed method is illustrated by means of an example.
Keywords |
| Machine Scheduling, Dynamic Programming Method, Type-2 Trapezoidal Fuzzy Numbers |
AMS Subject Classification |
| 94D05, 90-XX , Aug 2010 |
INTRODUCTION |
| The single machine scheduling problem with single processor (Machine) consists of single machine to process n-jobs. The jobs may be independent or dependent. An single machine scheduling problems can provide help and insight into resolving, understanding, managing and modeling more complex multi-machine scheduling problems. In this paper, we propose n-jobs to be processed on single machine scheduling problem (SMSP) involving type-2 trapezoidal fuzzy processing times and type-2 trapezoidal fuzzy due date. The different due date for each job be considered which meet the demand of customer with more satisfaction level. The main objective of this paper is to scheduling the job and minimizing the total tardiness. This method is become lucrative to make decision. In most of the real life problem, there are elements of uncertainty in process. In practical situation processing times and due date are not always deterministic. So, we have associated with fuzzy environment. Dynamic programming problem is the main concept of number of jobs is equal to number of stages. |
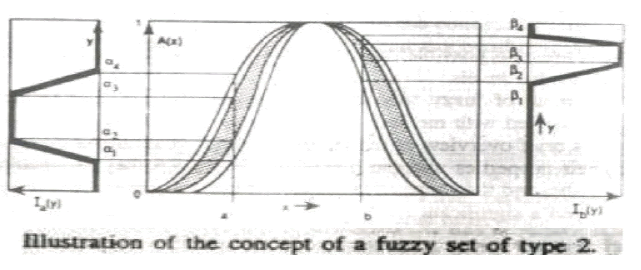
| The concept of a type-2 fuzzy set, which is an extension of the concept of an arbitrary fuzzy set, was introduced by Zadeh [15]. A fuzzy set is two dimensional and a type-2 fuzzy set is three dimensional, type-2 fuzzy sets can better improve certain kinds of inference than do fuzzy sets with increasing imprecision, uncertainty and fuzziness in information. A type-2 fuzzy set is characterized by a membership function, i.e., the membership value for each element of this set is a fuzzy set in [0,1], unlike an ordinary fuzzy set where the membership value is a crisp number in [0,1]. |
REVIEW OF LITERATURE |
| Various researchers have done a lot of work in different directions. Ishii and Tada [6] considered a single machine scheduling problem minimizing the maximum lateness of jobs with fuzzy precedence relations. Hong et.al., [5] introduced a single machine scheduling problem with fuzzy due date. Itoh and Ishii [7] proposed a single machine scheduling problem dealing with fuzzy processing times and due date. Gawiejnowiez et.al.,[2] deals with a single machine time dependent scheduling problem. Lawler [8] applied a dynamic programming approach to the single machine total tardiness problem. Uzsoy and Velasquez [13] addressed the problem of scheduling a single machine subject to family dependent set-up times in order to minimize maximum lateness. Graham and Lawler [4] introduced on single machine scheduling problem with non-zero ready times. Emmons [1] studied the single machine scheduling problem to minimize the total tardiness. Ghorhanali Mohammad [3] introduced the concept of single machine and the processing times of the jobs in fuzzy environment. |
| The paper is organized as follows: In section 2, deals with the preliminaries. In section 3, arithmetic operations on type-2 trapezoidal fuzzy number and ranking function are discussed. In section 4, we introduced a brief note on single machine scheduling problem. In section 5, the effectiveness of the proposed method is illustrated by means of an example. |
PRELIMINARIES |
 |
 |
 |
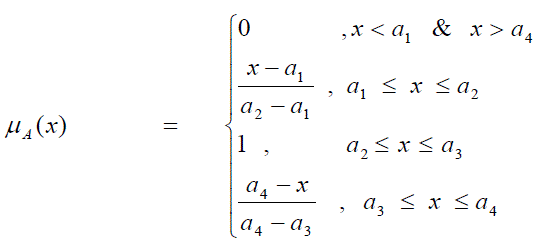 |
| Definition: Type-2 Trapezoidal Fuzzy Number |
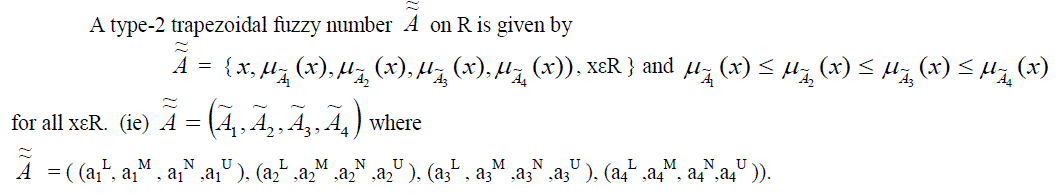 |
ARITHMETIC OPERATIONS |
Arithmetic Operations on Type-2 Trapezoidal Fuzzy Numbers |
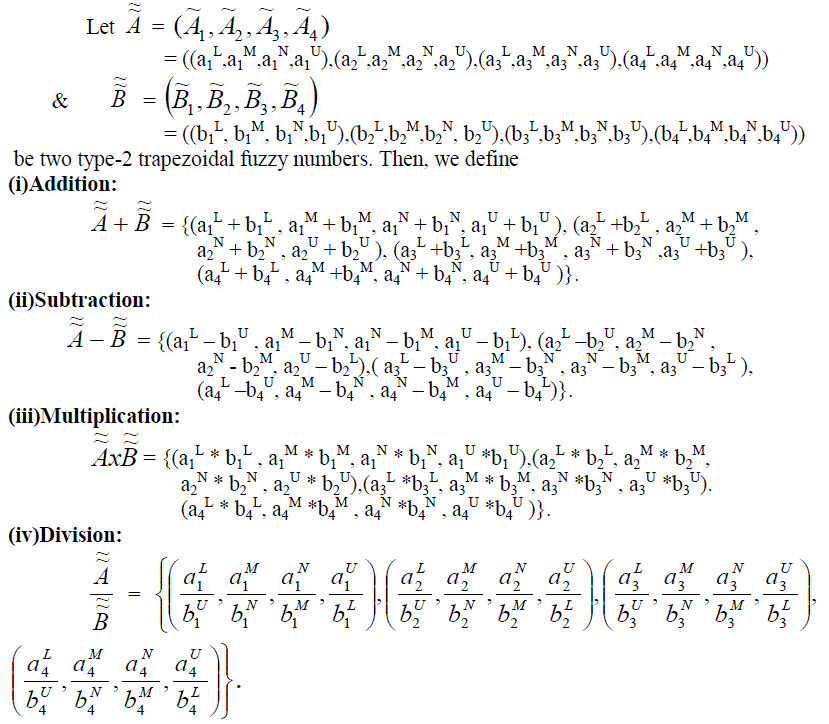 |
Ranking on Type-2 Trapezoidal Fuzzy Number |
| Let F( R ) be the set of all type-2 normal trapezoidal fuzzy numbers. One convenient approach for solving numerical valued problem is based on the concept of comparison of fuzzy numbers by use of ranking function. An effective approach for ordering the elements of F ( R ) is to define a linear ranking function R: F ( R ) → R which maps each fuzzy number into R. |
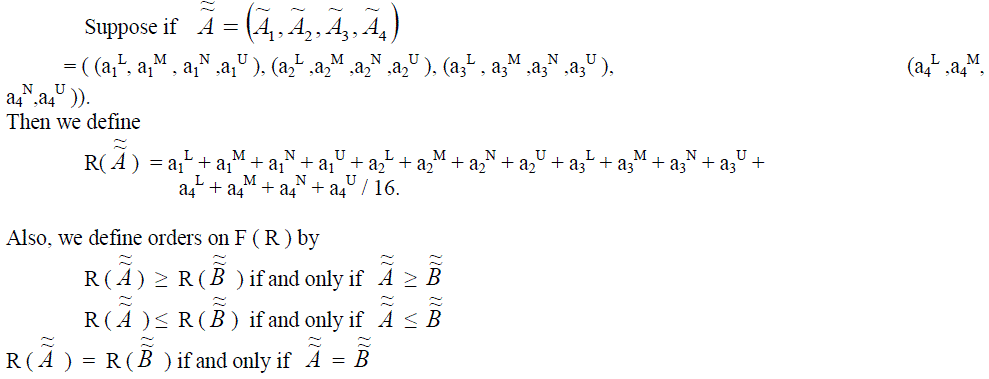 |
SINGLE MACHINE SCHEDULING PROBLEM |
Tardiness: |
| Tardiness is the lateness of job j if it fails to meet its due date; otherwise, it is zero. It is defined as : |
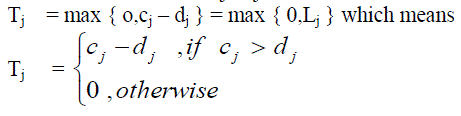 |
| Notations: |
 |
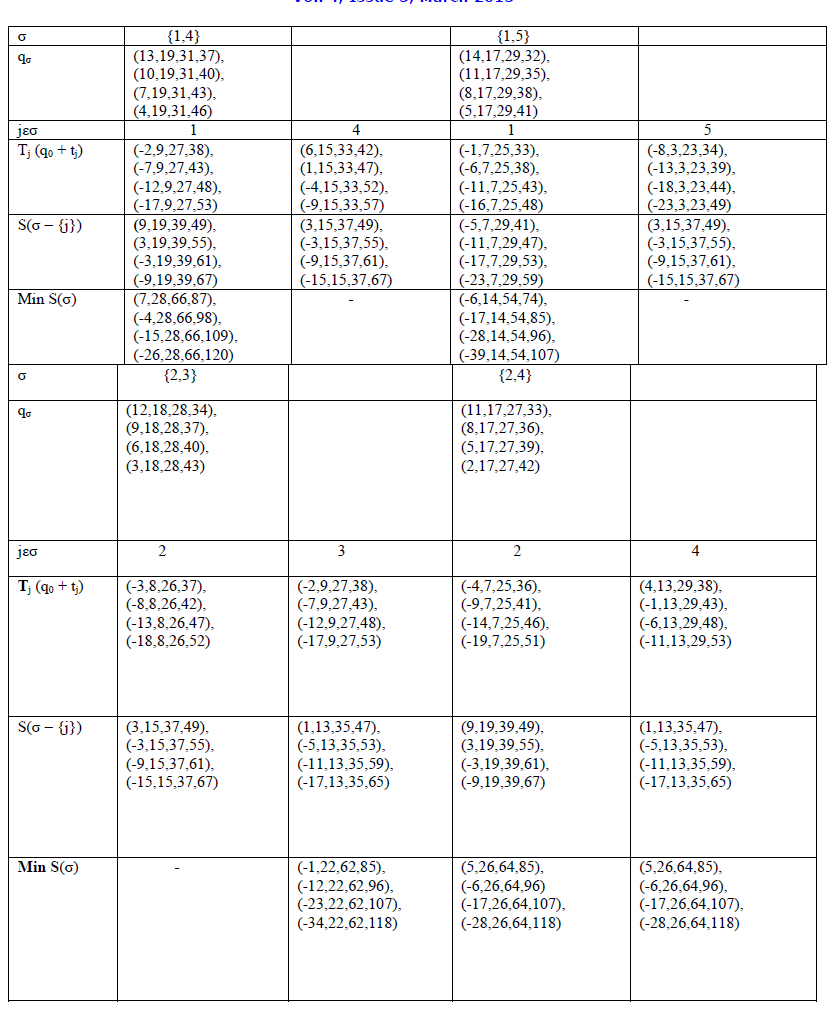
| Step-3: For σ = {1,2,3} in stage3, S(σ – {j}) for j = 1 is equal to the minimum of S(σ = 2,3) in stage2 where , σ contains the remaining jobs of σ in the current stage under consideration, that is {2,3}. |
| Step-4: For σ = { 1,2,3,5} in stage 4, S( σ – {j}) for j = 2 is equal to the minimum of S(σ = 1,3,5) in stage3 where, σ contains the remaining jobs of σ in the current stage under consideration, that is {1,3,5}. |
| Step-5: For σ = { 1,2,3,4,5} in stage 5, S(σ – {j}) for j = 5 is equal to the minimum of S(σ = 1,2,3,4) in stage 4 where, σ contains the remaining jobs of σ in the current stage under consideration, that is {1,2,3,4}. |
| NUMERICAL ILLUSTRATION |
| Consider a single machine scheduling problem in which each of the 5 jobs can be fully processed in the single machine. The type-2 trapezoidal fuzzy processing times and type-2 trapezoidal fuzzy due date for each jobs are given in the following table: |
| Table-1: |
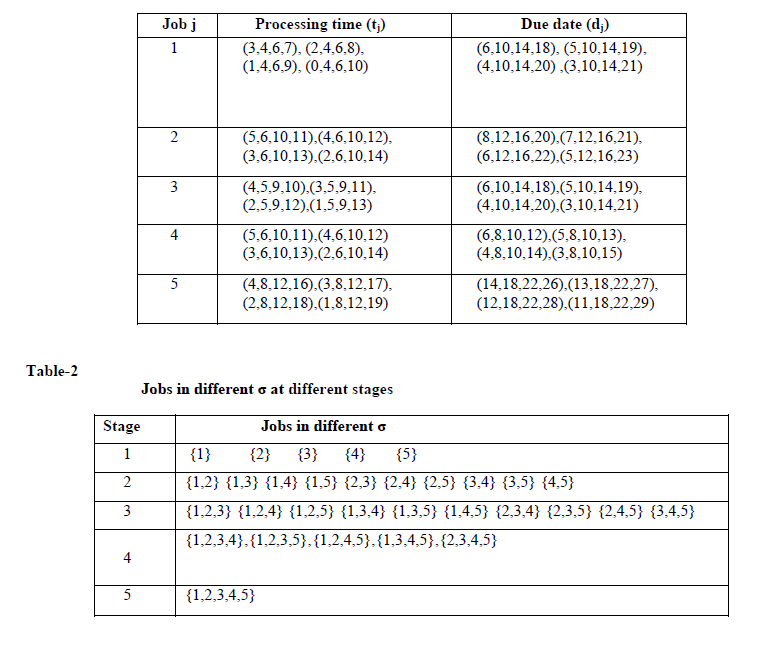 |
| Step-1: |
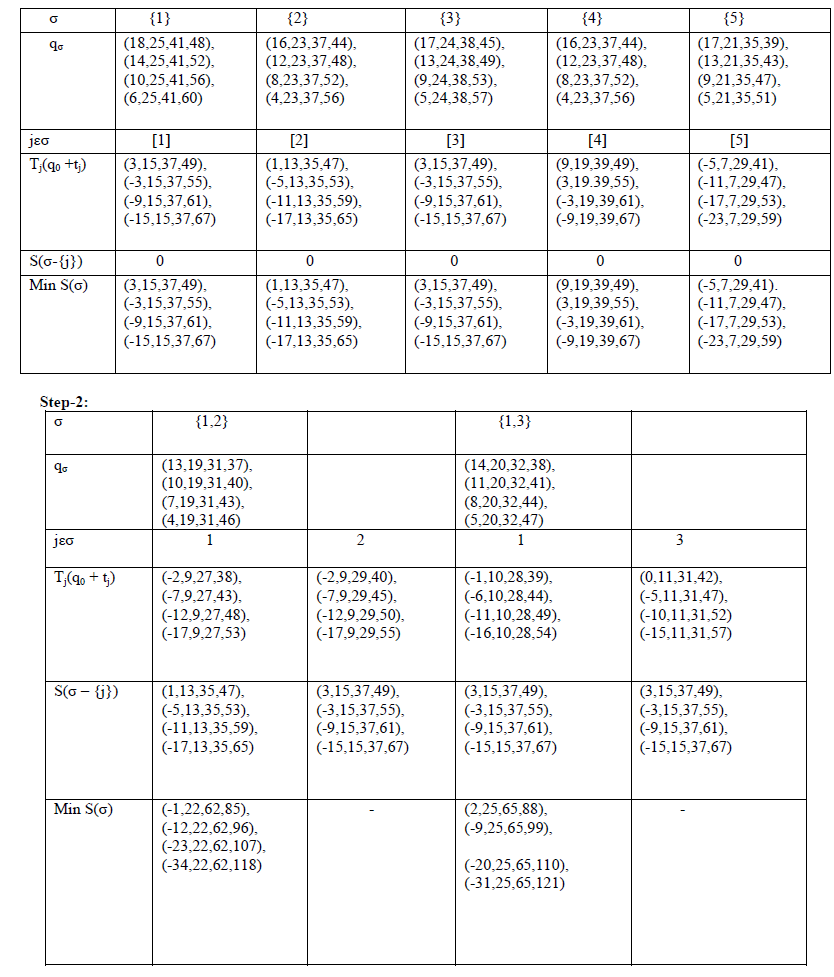 |
 |
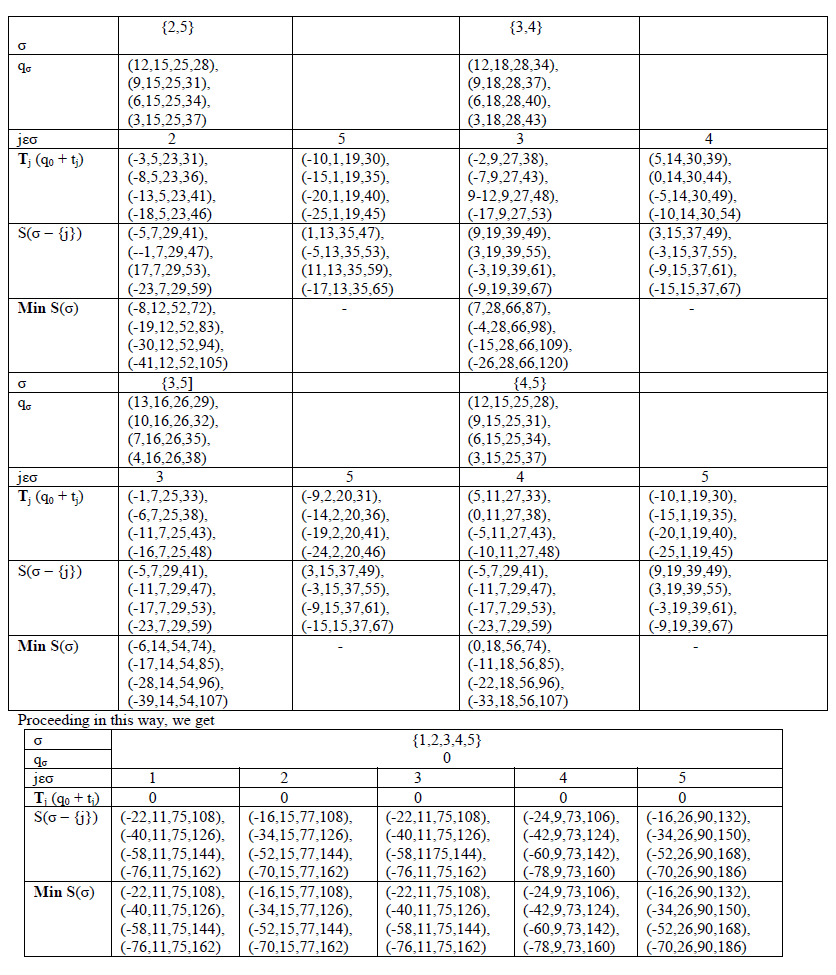 |
| Optimal Sequence of Jobs = 4 → 1 →3 → 2 → 5 |
| Minimum Total Tardiness = 41. |
CONCLUSION |
| We considered a single machine scheduling problem (SMSP) with fuzzy processing times and fuzzy due date to minimize the total tardiness. This method is very easy to understand each stage that will help the decision maker in determining a best schedule for a given set of jobs effectively. This method has significant use of practical results in industries. |
References |
|