ISSN: 2229-371X
ISSN: 2229-371X
| Sheetal Aggarwal1*, Ashok2 |
| Corresponding author: Sheetal Aggarwa, E-mail: saggarwal18@gmail.com1 |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at Journal of Global Research in Computer Sciences
In this paper we focus on some variants of K means clustering approach which can be used for image segmentation also. In k-means clustering, we are given a set of n data points in d-dimensional space and an integer k and the problem is to determine a set of k points in , called centers, so as to minimize the mean squared distance from each data point to its nearest center. A popular heuristic for k-means clustering is Lloyd's algorithm. In this paper we have analyzed and presented some extensions that increase its range of applicability.
Index terms |
| Clustering, K-means, Image segmentation, Fuzzy C-Means, Coreset |
INTRODUCTION |
| Clustering is the computational task to partition a given input into subsets of equal characteristics. These subsets are usually called clusters and ideally consist of similar objects that are dissimilar to objects in other clusters. This way one can use clusters as a coarse representation of the data. We loose the accuracy of the original data set but we achieve simplification.[1] Clustering has many applications in different areas of computer sciences such as computational biology, machine learning, data mining and pattern recognition. Since the quality of a partition is rather problem dependent, there is no general clustering algorithm. Consequently, over the years many different clustering algorithms have been developed. These algorithms can be characterized as hierarchical algorithms or partitioning algorithms. |
| Hierarchical algorithms build a hierarchy of clusters, i.e.every clusters is subdivided into child clusters, which form a partition of their parent cluster. Depending how the hierarchy is built we distinguish between agglomerative (bottomup) and divisible (top-down) clustering algorithms. |
| Partitioning algorithms try to compute a clustering directly. For example, they try to compute a clustering by iteratively swapping objects or groups of objects between the clusters or they try to identify dense areas containing many points. |
| The most prominent and widely used clustering algorithm is Lloyd’s algorithm sometimes also referred to as the k-means algorithm. The standard algorithm was first proposed by Stuart Lloyd in 1957. This algorithm requires the input set to be a set of points in the d-dimensional Euclidean space. Its goal is to find k cluster centers and a partitioning of the points such that the sum of squared distances to the nearest center is minimized. The algorithm is a heuristic that converges to a local optimum. The main benefit of Lloyd’s algorithm is its simplicity and its foundation on analysis of variances. Also, it is relatively efficient. The drawbacks are that the user must specify the number of clusters in advance, the algorithm has difficulties to deal with outliers and clusters that differ significantly in size, density, and shape. |
K-means Clustering Algorithm: |
| K-Means algorithm is an unsupervised clustering algorithm [2] that classifies the input data points into multiple classes based on their inherent distance from each other. The algorithm assumes that the data features form a vector space and tries to find natural clustering in them. The points are clustered around centroids |
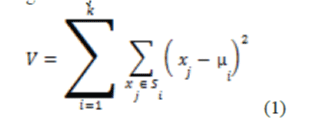 |
| Where there are k clusters, i = 1,2,…, k and is the centroid or mean point of all the points |
| As a part of this paper an iterative version of the algorithm is also presented here for image segmentation. The algorithm takes a 2 dimensional image as input. Various steps in the algorithm are as follows: |
| a. Compute the intensity distribution (also called the histogram) of the intensities. |
| b. Initialize the centroids with k random intensities. |
| c. Repeat the following steps until the cluster labels of the image do not change anymore. |
| d. Cluster the points based on distance of their intensities from the centroid intensities. |
| Where k is a parameter of the algorithm (the number of clusters to be found), i iterates over the all the intensities, j iterates over all the centroids and are the centroid intensities. |
SOME VARIANTS OF K-MEANS |
Coresets: |
| The novel feature of algorithm [1] is that it uses coresets to speed up the algorithm. A coreset is a small weighted set of points that approximates the original point set with respect to the considered problem. The main strength of the algorithm is that it can quickly determine clusterings of the same point set for many values of k. This is necessary in many applications, since, typically, one does not know a good value for k in advance. Once we have clusterings for many different values of k we can determine a good choice of k using a quality measure of clusterings that is independent of k, for example the average silhouette coefficient. The average silhouette coefficient can be approximated using coresets. |
| To evaluate the performance of this algorithm it is compared with algorithm KMHybrid on the basis of setup times for both algorithms. KMHybrid combines swapping of centers with Lloyd’s algorithm and a variant of simulated annealing. |
| It has been shown that the setup time for KMHybrid is between 1.5 to 7 times higher than that of CoreMeans. There is a tendency that the gap becomes larger for larger instances. |
Accelerated k-means: |
| K-means is considered a fast method because it is not based on computing the distances between all pairs of data points. However, the algorithm is still slow in practice for large datasets. The number of distance computations is nke where n is the number of data points, k is the number of clusters to be found, and e is the number of iterations required. Empirically, e grows sublinearly with k and n, and the dimensionality d of the data. |
| Accelerated k-means is an optimized version of the standard k-means method, with which the number of distance computations is in practice closer to n than to nke. |
| The optimized algorithm is based on the fact that most distance calculations in standard k-means are redundant. For example, if a point is far away from a center, it is not necessary to calculate the exact distance between the point and the center in order to know that the point should not be assigned to this center. |
| The accelerated algorithm [3] avoids unnecessary distance calculations by applying the triangle inequality in two different ways, and by keeping track of lower and upper bounds for distances between points and centers. Experiments has also been done which show that the new algorithm is effective for datasets with up to 1000 dimensions, and becomes more and more effective as the number k of clusters increases. |
Fast Hybrid K-Means for Segmentation: |
| Segmentation is the art of automatically separating an image into different regions in a fashion that mimics the human visual system. It is therefore a broad term that is highly dependent on the application at hand, e.g. one might want to segment each object individually, groups of objects, parts of objects, etc.. In order to segment a particular image, one must first identify the intended result before a set of rules can be chosen to target this goal. The human eye uses low-level information such as the presence of boundaries, regions of different intensity or colors, brightness and texture, etc., but also mid-level and high-level cognitive information, for example, to identify objects or to group individual objects together. As a direct consequence, there are a wide variety of approaches to the segmentation problem, and many successful algorithms have been proposed and developed to simulate a number of these different processes. |
| The algorithm [4], first draws a connection between a level set algorithm and k-Means plus nonlinear diffusion preprocessing. Then, exploit this link is exploited to develop a new hybrid numerical technique for segmentation that draws on the speed and simplicity of k-Means procedures, and the robustness of level set algorithms. The proposed method retains spatial coherence on initial data characteristic of curve evolution techniques, as well as the balance between a pixel/voxel’s proximity to the curve and its intention to cross over the curve from the underlying energy. However, it is orders of magnitude faster than standard curve evolutions. Moreover, it does not suffer from the limitations of k-Means due to inaccurate local minima and allows for segmentation results ranging from k-Means clustering type partitioning leveling set partitions. Results are shown in Fig.1.[4] |
Constrained K-Means Clustering: |
| Clustering algorithms are generally used in an unsupervised fashion. They are presented with a set of data instances that must be grouped according to some notion of similarity. The algorithm has access only to the set of features describing each object; it is not given any information (e.g., labels) as to where each of the instances should be placed within the partition. |
| Clustering is traditionally viewed as an unsupervised method for data analysis. However, in some cases information about the problem domain is available in addition to the data instances themselves. Researchers have demonstrated [5] how the popular k-means clustering algorithm can be profitably modified to make use of this information. Experiments has been done with artificial constraints on six data sets, and improvements have been observed in clustering accuracy. This method is also applied to the real-world problem of automatically detecting road lanes from GPS data and results in dramatic increases in performance. |
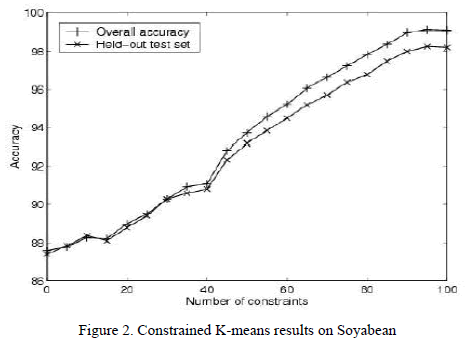 |
| Without any constraints, the k-means algorithm achieves an accuracy of 87% (see Fig. 2[5]). Overall accuracy steadily increases with the incorporation of constraints, reaching 99% after 100 random constraints. |
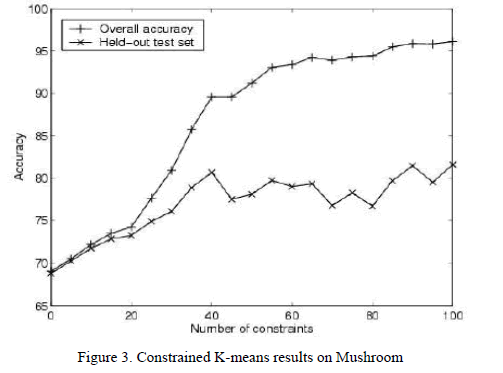 |
| In the absence of constraints, the k-means algorithm achieves an accuracy of 69% (Fig. 3[5]). After incorporating 100 random constraints, overall accuracy improves to 96%. |
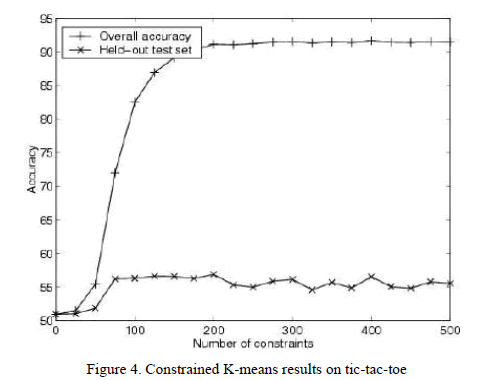 |
| Without constraints, the k-means algorithm achieves an accuracy of 51% (Fig. 4[5]). After incorporating 500 random constraints, overall accuracy is 92%. |
K-Means Clustering for Color Image Segmentation: |
| Segmentation is a process to partition the image into multiple regions which intended to extract the object from a background. Common segmentation approaches are intensity-based, color-based, and shaped-based segmentation. |
| The goal of image segmentation is to cluster pixels into salient image regions, i.e., regions corresponding to individual surfaces, objects, or natural parts of objects. |
| There are many methods of clustering developed for a wide variety of purposes. Clustering algorithms used for unsupervised classification of remote sensing data vary according to the efficiency with which clustering takes place. K-means is the clustering algorithm used to determine the natural spectral groupings present in a data set. This accepts from analyst the number of clusters to be located in the data. The algorithm then arbitrarily seeds or locates, that number of cluster centres in multidimensional measurement space. Each pixel in the image is then assigned to the cluster whose arbitrary mean vector is closest. The procedure continues until there is no significant change in the location of class mean vectors between successive iterations of the algorithms. As K-means approach is iterative, it is computationally intensive and hence applied only to image subareas rather than to full scenes and can be treated as unsupervised training areas. |
| An approach [2] is given for image segmentation. This approach works by transforming the image to HSV color space and grouping the pixel using K-mean clustering. |
| There is a two-phase iterative algorithm to minimize the sum of point-to-centroid distances. |
| a. Batch updates: each iteration consists of reassigning points to their nearest cluster centroid, all at once, followed by recalculation of cluster centroids. |
| b. Online updates: points are individually reassigned; in doing so the sum of distances is reduced, and cluster centroids are recomputed after each reassignment. Each iteration during this second phase consists of one passing through all the points. K-means can converge to a local optimum, in this case, a partition of points in which moving any single point to a different cluster increases the total sum of distances. |
 |
Optimized Fuzzy C-Means Clustering: |
| Fuzzy C-Means Clustering algorithm (FCM) is a method that is frequently used in pattern recognition. It has the advantage of giving good modeling results in many cases, although, it is not capable of specifying the number of clusters by itself [7]. In FCM algorithm most researchers fix weighting exponent (m) to a conventional value of 2 which might not be the appropriate for all applications. The subtractive clustering algorithm is used to provide the optimal number of clusters needed by FCM algorithm by optimizing the parameters of the subtractive clustering algorithm by an iterative search approach and then to find an optimal weighting exponent (m) for the FCM algorithm. In order to get an optimal number of clusters, the iterative search approach is used to find the optimal single-output Sugeno-type Fuzzy Inference System (FIS) model by optimizing the parameters of the subtractive clustering algorithm that give minimum least square error between the actual data and the Sugeno fuzzy model. Once the number of clusters is optimized, then two approaches are proposed to optimize the weighting exponent (m) in the FCM algorithm, namely, the iterative search approach and the genetic algorithms. The above mentioned approach is also tested on the generated data from the original function and optimal fuzzy models are obtained with minimum error between the real data and the obtained fuzzy models. |
CONCLUSION |
| We have discussed various k-means clustering algorithms for both datasets and image segmentation. An image can be treated as a set of datapoints ( intensity, texture, color, shape) and image segmentation can be treated as clustering of similar datapoints. So, the approaches for dataset can also be used for image segmentation. |
References |
|