ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
V.Prasanth, Rubia Tasneem
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Advancement in the VlSI technology using low power, less area and high speed constraints is mostly used for encoding and decoding of data. In this paper power and cost reduction with increase in speed using viterbi decoder(VD) for trellis coded modulation(TCM) is proposed. Viterbi decoder uses viterbi algorithm for TCM decoding, but the efficient speed and power reduction is not achieved at the receiving ends. A pipelined architecture with a pre-computational approach which incorporated T-algorithm for VD is proposed in this paper. Priority encoder is used along with convolution encoders to send data bits of high priority first with a code rate of ½ in TCM system. The proposed architecture reduces power consumption of 80% without performance loss. The degradation of clock speed used in the architecture is negligible. Proposed architecture is simulated and synthesized using Xilinx ISE successfully and analyzed using FPGA Spartan-6 XC6SLX45 which is a low power target device. The results obtained are found to be consuming low power.
Keywords |
| Priority encoder, Spartan-6 XC6SLX45, Trellis coded modulation (TCM), Viterbi decoder. |
INTRODUCTION |
| The decoding process for convolution codes in memory less noise systems is done by using viterbi algorithm proposed by viterbi. For the host problem encountered in the communication systems this algorithm can be applied. Many band efficient systems employ Trellis coded modulation technique[1].A high-rate convolution code, which leads to a high complexity of the viterbi decoder (VD) for the TCM decoder, even if the constraint length of the convolution code is moderate is employed in TCM systems. For example, the rate -3/4 convolution code used in a 4-D TCM system for deep space communications [2] has a constraint length of 7; however, the computational complexity of the corresponding VD is equivalent to that of a VD for a rate-1/2 convolution code with a constraint length 9 due to the large number of transitions’ in the trellis. |
| The viterbi decoder in TCM decoders is dominant module in terms of power consumption. To reduce the computational complexity as well as power consumption, low-power schemes should be exploited for the VD in a TCM decoder. The General solutions for low-power VD designs have been well studied by existing work. power reduction in VDs could be achieved by reducing the number of states for example, reduced-state sequence decoding(RSSD)[3].M-algorithm[4] and T-algorithm[5] or[6] by over scaling the supply voltage[7].The whole system that includes the VD should be taken into consideration for over-scaling the supply voltage, which is not main focus of our research. M-algorithm in practical applications is efficient algorithm compared to RSSD[3],because the M-algorithm requires a sorting process in a feedback loop while T-algorithm only searches for the optimal path metric(PM),that is the minimum value or the maximum value of all PMs. |
 |
| For reducing the power consumption T-algorithm has been shown to be very efficient. [8], [9]. However, searching for the optimal PM in the feedback loop still reduces the decoding speed which is a drawback. To overcome this two variations of the T -algorithm have been proposed: the relaxed adaptive VD [8], which suggests using an estimated optimal PM, instead of finding the real one each cycle and the limited-search parallel state VD based on scarce state transition (SST) [9]. In our preliminary work [10], we have shown that when convolution codes of high rate are applied the relaxed adaptive VD suffers a severe degradation of bit-error-rate (BER) due to which performance inherent drifting error occurs between the estimated optimal PM and the accurate one. On the other hand, the SST based scheme requires pre-decoding and re-encoding processes and is not suitable for TCM decoders. The encoded data are always associated with a complex multi-level modulation scheme like 8-ary phase-shift keying (8PSK) or 16/64-ary quadrature amplitude modulation (16/64QAM) through a constellation point mapper in TCM scheme. A soft-input VD should be employed at the receiver to guarantee a good coding gain. Due to which pre-decoding and re-encoding of the TCM signal along with the computational overhead and decoding latency become high. In our preliminary work [10], based on pre-computation, an add-compare-select unit (ACSU) architecture for VDs incorporating T –algorithm was proposed, which efficiently improves the clock speed of a VD with T -algorithm for a rate-3/4 code. In this work, we further analyze the pre-computation algorithm. A systematic way to determine the optimal pre-computation steps is presented, where the minimum number of steps for the critical path to achieve the theoretical iteration bound is calculated and the computational complexity overhead due to pre-computation is evaluated. Then, we discuss a complete low-power high-speed VD design for the rate-3/4 convolution code [2]. Finally low power fpga implementation results of the VD are reported, which have not been obtained in our previous work in [10]. |
| The remainder of this paper is organized as follows. Section II Gives the background information of VDs. Section III presents the pre-computation architecture with T-algorithm and also discusses the choice of pre- computation steps. Details of a design example including the modification of survivor-path memory unit (SMU) are discussed in Section III. Synthesis and power estimation results are reported in Section IV and conclusions are given in Section V. T - algorithm and discusses the choice of pre- computation steps. Details of a design example including the modification of survivorpath memory unit (SMU) are discussed in Section III. Synthesis and power estimation results are reported in Section IV and conclusions are given in Section V. |
VITERBI DECODER |
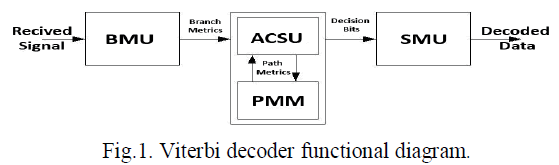
| A typical Viterbi decoder functional block diagram is shown in Fig. 1. First, in the BM unit BMU branch metrics (BMs) are calculated from the received symbols. This module is replaced by transition metrics unit (TMU) in a TCM decoder, which is more complex than the BMU .Then, BMs are fed into the ACSU that recursively which computes the PMs and outputs decision bits for each possible state transition. After that, the decision bits are stored in they are retrieved from the SMU in order to decode the source bits along the final survivor path. The PM unit (PMU) stores the PMs of the current iteration. An extra computation in the ACSU loop for calculating the optimal PM and puncturing states is required in T -algorithm. Due to which, a straight- forward implementation of T-algorithm will dramatically reduce the decoding speed ,The key point of improving the clock speed of T -algorithm is to quickly find the optimal PM. |
PRECOMPUTATION ARCHITECTURE |
A. Pre-computation Algorithm |
| The pre-computation algorithm idea was presented in [9]. Consider a convolution code for VD with a constraint length of k, where each state receives p candidate paths. First, we expand PMs at the current time slot n(PMs(n)) as a function of n(PMs(n-1)) to form a look-ahead computation of the optimal PM-PM opt(n). If the branch metrics are calculated based on the Euclidean distance, |
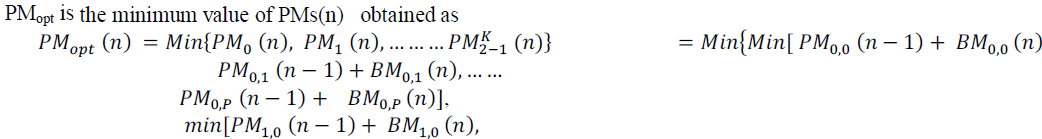 |
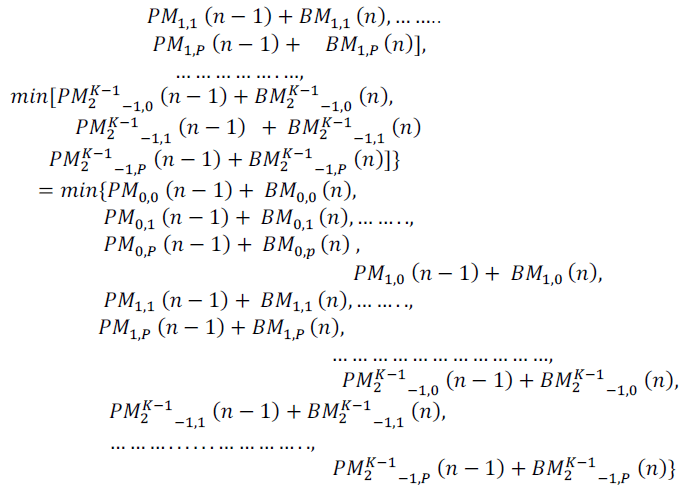 |
 |
| Then, the states are grouped into several clusters in order to decrease the computational overhead caused by look-ahead computation. Usually the trellis butterflies have a symmetric structure for VD. In other words, the states can be grouped into clusters, where all the clusters have the same number of states and all the states in the same cluster will be extended by the same BMs. |
| Thus, (1) can be rewritten as: |
 |
| For each cluster the min(BMs) can be easily obtained from the BMU or TMU and the min(PMs) at time n -1 in each cluster at the same time they can be pre-calculated when the ACSU is updating the new PMs for time n. Theoretically, when we continuously decompose PMs(n - 1); PMs(n - 2); . .. . ., the pre-computation scheme can be extended to q steps, where q is any positive integer that is less than n.Hence, PMopt(n) can be calculated directly from PMs(n-q) in q cycles |
B. Selection of Pre-computation steps |
| In [9], we have shown through a design example that, q-step pre-computation can be pipelined into q stages, As q increases the logic delay of each stage is continuously reduced. As a result, the decoding speed of the low-power VD is greatly improved. However, after reaching a certain number of steps, qb, further pre-computation would not result in additional benefits because of the inherent iteration bound of the ASCU loop.Therefore it is worth to discuss the optimal number of pre-computation steps. In TCM system, the convolution code usually has a coding rate of R/R+1,R=2,3,4,..............so that in (1),p=2R and the logic delay of the ACSU is TACSU=Tadder+Tp-in-comp where Tadder is the logic delay of the adder to compute PMs of each candidate path that reaches the same state and Tp-in-comp is the logic delay of a p-input comparator to determine the survivor path(the path with minimum metric) for each state., the iteration bound is slightly longer than TACSU because there will be another two-input comparator in the loop to compare the new PM and a preset T as shown below if T-algorithm is employed in the VD (3) |
 |
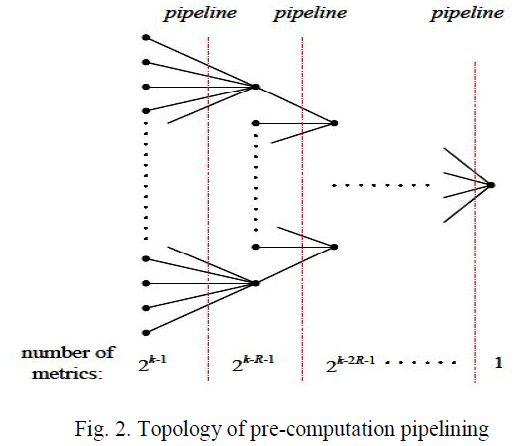
| In each pipelining stage to achieve the iteration bound expressed in(3),for the pre-computation, we limit the comparison to be among only p or 2p metrics. To simplify our evaluation ,we assume that each stage reduces the number of metrics to 1/p(or2-R) of its input metric as shown in fig.2.The smallest number of pre computation steps(qb) meeting the theoretical iteration bound should satisfy (2R)qb≥2k-1.Therefore,qb≥(k-1)/R and qb is expressed as (4),where âÃâÃâ.âÃâÃâdenotes the ceiling function |
| In design example shown in [9], with coding rate of ½ and constraint length of 7, the minimum pre computation steps for VD to meet the iteration bound is 2 according to (4).It is the same value as we obtained from direct architecture design[9].In some cases, the number of remaining metrics may slightly expand during a certain pipeline stage after addition with BMs. The extra delay can be absorbed by an optimized architecture or circuit design usually,. Even it is hard to eliminate the extra delay, the resultant clock speed is much closer to the theoretical bound. we could add another pipeline stage, to fully achieve the iteration bound, though it is very costly as will be shown next. Computational overhead (compared with conventional T -algorithm) is an important factor that should be carefully evaluated. The most computational overhead comes from adding BMs to the metrics at each stage as indicated in (2). In other words, if there are m remaining metrics after comparison in a stage, the computational overhead from this stage is at least m addition operations. The exact overhead varies from case to case based on the convolution code’s trellis diagram. Again, we consider a code with a constraint length k and q pre-computation steps to simplify the evaluation. Also, we assume that each remaining metric would cause a computational overhead of one addition operation. In this case, the number of metrics will reduce at a ratio of 2(k-1)/q and the overall computational overhead is (measured with addition operation). |
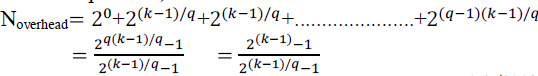 |
| The estimated computational overhead according to (5) is 63/(26/q -1) when k = 7 and q ≤ 6, which increases almost exponentially to q . In a real design, the overhead increases even faster than what is given by (5) when other factors (such as comparisons or expansion of metrics as we mentioned above) are taken into consideration. Therefore, a small number of pre-computational steps is preferred even though the iteration bound may not be fully satisfied. The good choice in most cases one or two-step pre-computation. The above analysis also reveals that pre-computation is not a good option for low-rate convolution codes (rate of 1/Rc; Rc = 2; 3; . . .), because it usually needs more than two steps to effectively reduce the critical path (in that case, R = 1 in (4) and qb is k - 1). The two steps of pre-computation could achieve the iteration bound or make a big difference in terms of clock speed where high-rate convolution codes are employed for TCM systems. Due to which, the computational overhead is small. |
LOW-POWER HIGH-SPEED VITERBI DECODER DESIGN |
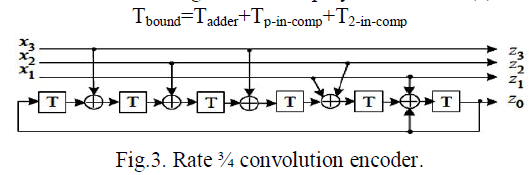
| We are still using the 4-D8PSK TCM system as described in [2] as example. The rate-3/4 convolution code employed in the TCM system is shown in Fig.3.Preliminary BER performance and architecture design for the ACSU unit have been discussed in [10].In section, we further address the SMU design issue the code rate ½ is employed. Later in the next section, we report various FPGA family implementation results that have not been obtained before. |
| BER performance of the VD employing T-algorithm with different values of T over an additive white Gaussian noise channel is shown in Fig.4.The simulation is based on a 4-D 8PSK TCM system employing the rate3/4 code |
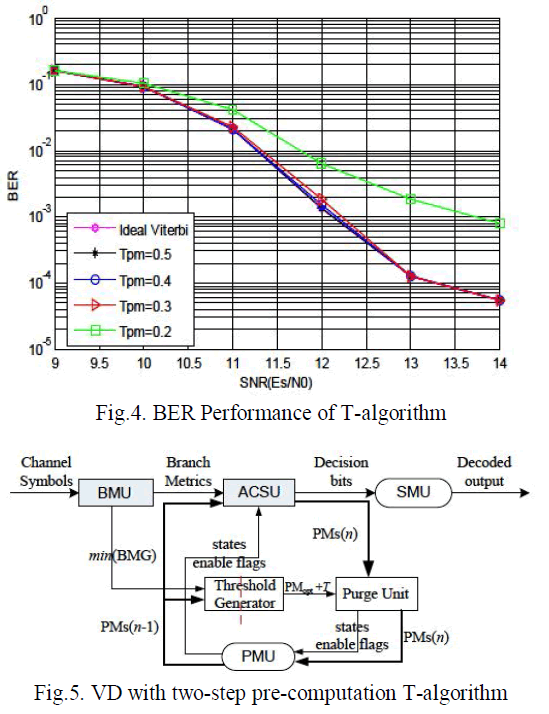 |
| The overall coding rate is 11/12 after due to other unencoded bits in TCM system. Compared with ideal viterbi algorithm, the threshold “T pm”can be lowered to 0.3 with less than 0.1db of performance loss; while the computational complexity could be reduced by upto 90% ideally .Since the performance is the same as that of convectional T-algorithm |
A.ACSU Design |
| We have concluded that two-step pre-computation is the optimal choice for the rate-3/4 code VD. For convenience of discussion, we define the left-most register in Fig.3as the most significant bit(MSB) and the rightmost register as the least significant-bit(LSB).The 64 states and PMs are labeled from 0 to 63.The two-step pre-computation is expressed as |
 |
 |
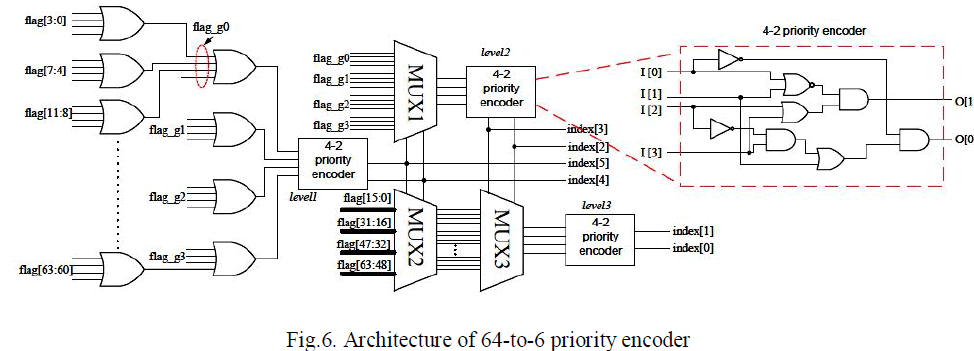
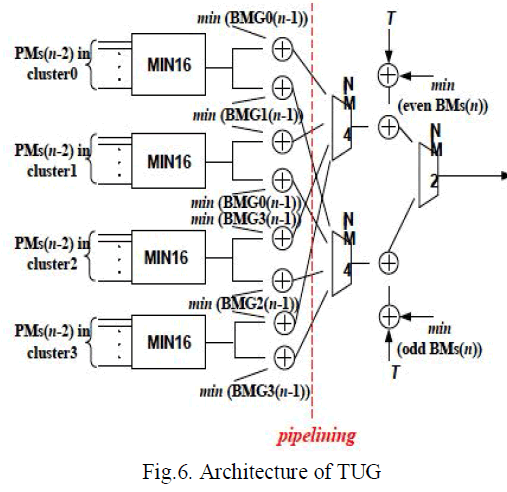
| The VD with two-step pre-computation T-algorithm functional block diagram is shown in fig.5. The minimum value of each BM group(BMG) is calculated in BMU or TMU and then passed to the “Threshold Generator “unit (TGU) to calculate (PMopt+T). The new PMs and (PMopt+T) are then compared in the “purge unit”(PU).The architecture of the TUG is shown in Fig6 in, which the key functions of the two-step pre-computation scheme are implemented. In Fig.6,the “MIN 16” unit for finding the minimum value in each cluster is constructed with two stages of four-input comparators. To meet the iteration bound this architecture has been optimized, compared with the convectional Talgorithm ,the computational overhead of this architecture is 12 addition operations and a comparison, which is slightly more than the number obtained from the evaluation(5). |
B. SMU Design |
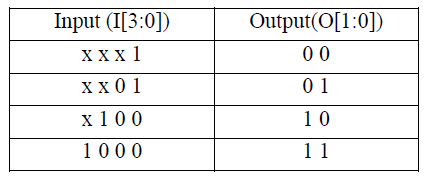
| An important issues regarding SMU design when T-algorithm is employed in this section is addressed. Two different types of SMU in the literature: register exchange (RE) and the trace back (TB) schemes are there. The SMU always outputs the decoded data from a fixed state in the regular VD without any low power schemes (arbitrarily selected in advance) if RE scheme is used, or traces back the survivor path from the fixed state if TB scheme is used, for lowcomplexity purpose. For VD in-corporate with T-algorithm, no state is guaranteed to be active at all clock cycles. Thus it is not possible to appoint a fixed state for either outputting the decoded bit (RE scheme) or starting the traceback process(TB scheme).In the implementation of convectional T-algorithm, the optimal state (state with PMopt) can be used by the decoder, which is always enabled, to output or trace back data. The process of searching for PMopt can find out the index of the optimal state as a byproduct. However, when the estimated PMs at the previous time slot, it is difficult to find the index of the optimal state. A practical method is to find index of an enabled state through a 2(k-1) to –(k-1) priority encoder. Suppose that we have labeled the states from 0 to 63.The output of the priority encoder would be the unpurged state with the lowest index. Assuming the other states are assigned the flg”1” and purged states have the flag”0”,the truth table of such priority encoder is shown in table1,where the “flag” is the input and “index” is the output |
 |
C. Threshold Generator Unit |
| To generate the threshold value a threshold generator unit is used which will take maximum or minimum value at each stage. It is not trivial to implement such a table. We employ an efficient architecture for 64-to-6 priority encoder based on three 4-to-2 priority encoders in our design, as shown in the below Fig 7.The 64 flags each of which contains 16 flags are first divided into 4 groups,. The priority encoder which is at level 1 detects which group contains at least one”1” and determines index[5:4]”.Then MUX2 selects one group of flags based on ”index[5:4]”.The input of the priority encoder which is at level2 can be computed from output of MUX2 by “or” operations. By introducing another MUX (MUX1) we can reuse the intermediate results. The output of the priority encoder which is at level 2 is “index[3:2]”.Again “index[3:2]” selects four flags (MUX3) as input of the priority encoder level 3. Finally, the last encoder will determine “index [1:0]”.Implementing the 4-to-2 priority encoder is much simpler than implementing the 64-to-6 priority encoder. Its truth table is shown in Table II and corresponding logics are shown in (7) and (8) |
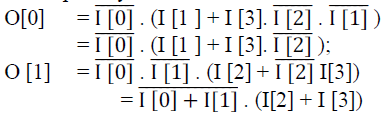 |
 |
 |
IMPLEMENTATION RESULTS |
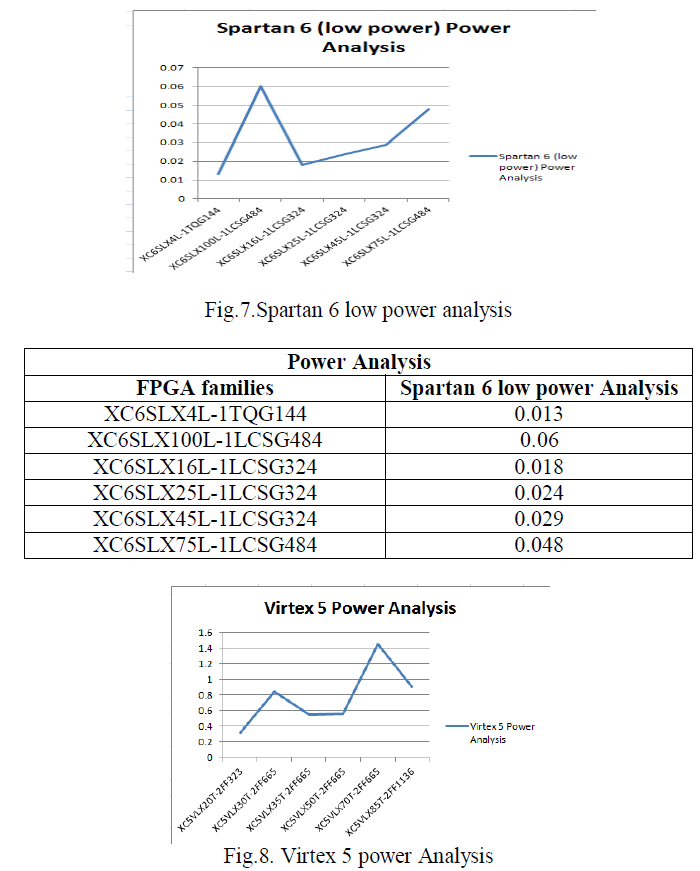 |
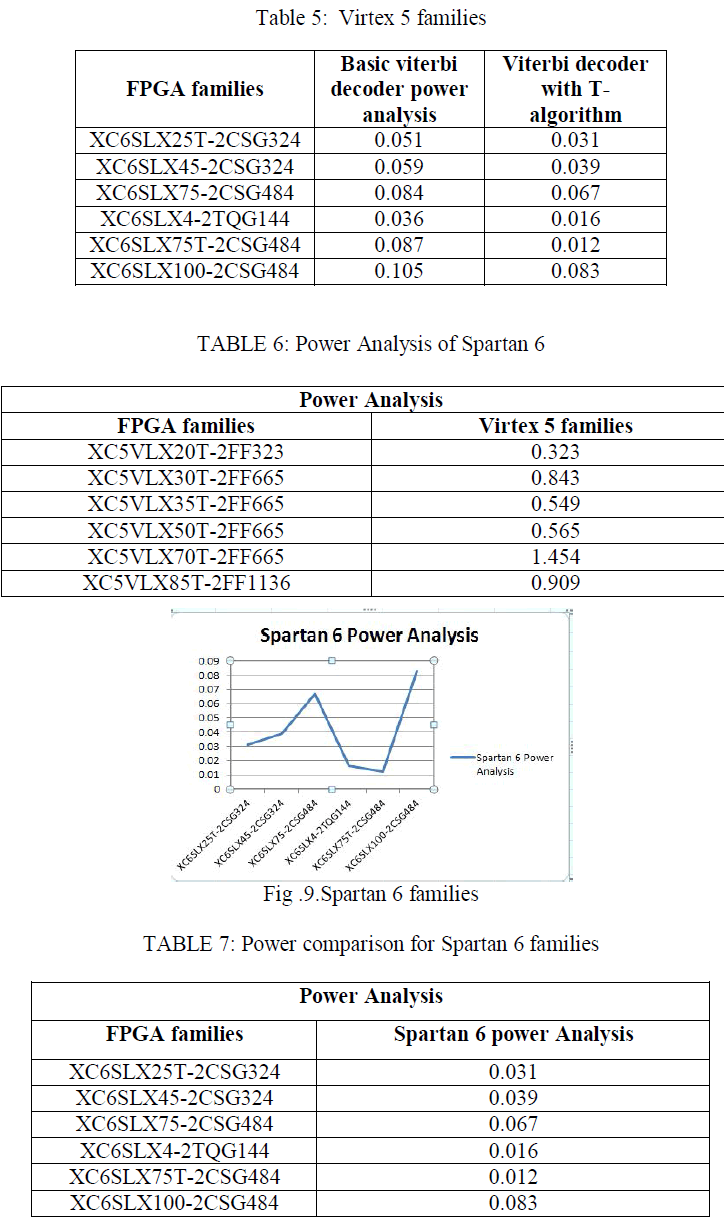 |
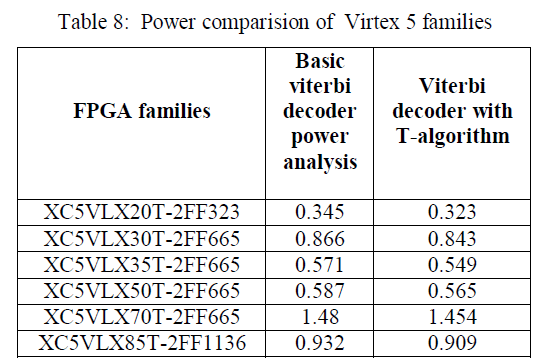 |
Simulation Result |
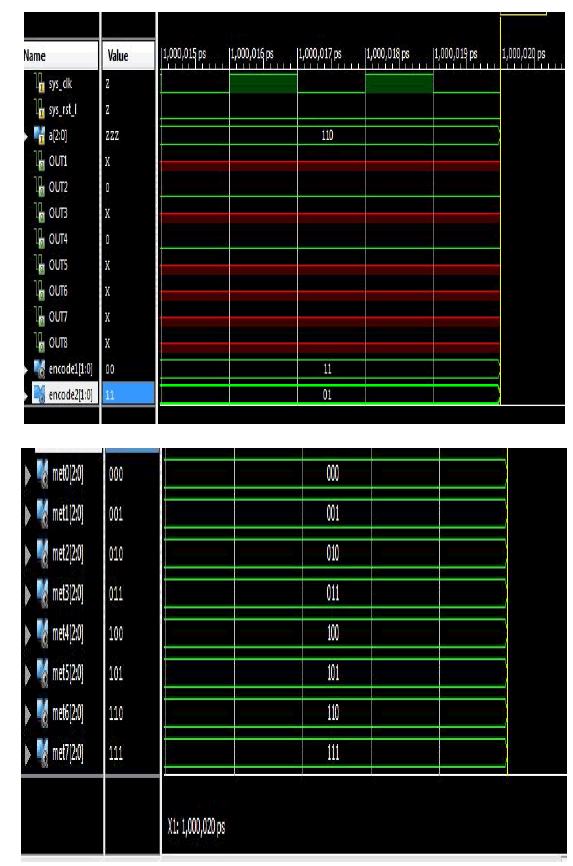 |
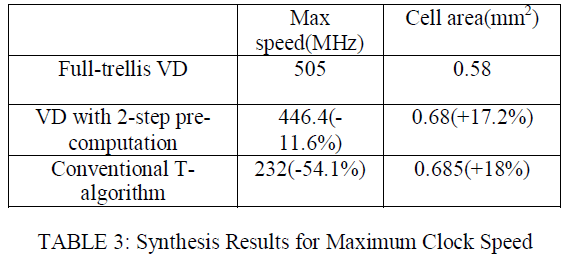
| The full-trellis VD, the VD with the two-step pre-computation architecture and one with the conventional T-algorithm are modeled with Verilog HDL code.The soft inputs of all VDs are quantized with 7 bits.Each PM in all VDs is quantized as 12 bits.RE scheme with survival length of 42 is used for SMU and the register arrays associated with the purged states are clock-gated to reduce the power consumption in SMU.For ASIC synthesis, We use TSMC 90-nm CMOS standard cell. The synthesis targets to achieve the maximum clock speed for each case and the result are shown in table III |
| Table II shows that the VD with two-step pre-computation architecture only decreases clock speed by 11% compared with the full-trellis VD. Mean while, the increase of the hardware area is about 17%.Thee decrease of clock speed is inevitable since the iteration bound for VD with T-algorithm is inherently longer than that of full-trellis VD. Also, any kinds of low-power scheme would introduce extra hardware like purge unit shown in Fig5 or the clockgating module in the SMU. Therfore, the hardware overhead of the proposed VD is expected. On the other hand, the VD with conventional T-algorithm cannot achieve half of the clock speed of the full trellis VD. |
| Therefore, for high-speed applications, it should not be considered. It is worth to mention that the conventional Talgorithm VD takes slightly more hardware than proposed architecture, which is counterintuitive. This is because the former decoder has much longer critical path and the synthesis tool took extra measures to improve clock speed. It is clear that the conventional T-algorithm is not suitable for high-speed applications. If the target throughput is moderately high proposed architecture can operate at a lower supply voltage |
| which is counterintuitive. This is because the former decoder has much longer critical path and the synthesis tool took extra measures to improve the clock speed. It is clear that the conventional T-algorithm is not suitable for high speed application. If the target throughput is moderately high, the proposed architecture can operate at lower supply voltage, which will lead to quadratic power reduction compared to the conventional scheme. Thus we next focus on power comparison between the full trellis VD and the proposed scheme. |
| We estimate the power consumption of these two designs with synopsis prime Power under the clock speed of 200Mb/s(power supply of 1.0 V,temperature of 300K).A total of 1133 received symbols(12000 bits) are simulated. The results are shown in table IV. |
| With the finite word-length implementation, the threshold can only be changed by a step of 0.125.Therfore, to maintain a good BER performance, the minimum threshold we chose is 0.375.Table IV shows that, as the threshold decreases, the power consumption of the proposed VD is reduced accordingly. In order to achieve the same BER performance, the proposed VD only consumes 30.8% the power of the full-trellis VD. |
CONCLUSION |
| We have proposed a high-speed low power VD design for TCM systems. The pre-computation architecture that incorporates T-algorithm efficiently reduces the power consumption of VDs without reducing the decoding speed appreciably. We have also analyzed the pre-computation algorithm, where the optimal pre-computation steps are calculated and discussed. The algorithm is suitable for TCM systems which always employ high-rate convolution codes. Finally, we presented a design case. Both the ACSU and SMU are modified to correctly decode the signal.ASCI synthesis and power estimation results show that, compared with full-trellis VD without a low-power scheme, the precomputation VD could reduce the power consumption by 80%with only 11% reduction of the maximum decoding speed. |
References |
|