ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
N.M.Mary Sindhuja1, A.S.Arumugam2,
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Hyper spectral images are image data consisting of hundreds of spectral bands leading to very large raw data size. Hyper spectral images are usually captured by satellites that use embedded processors with limited resources, so encoding complexity is critical. The space borne sensors cannot store all the data and need to transmit them to a ground station, there is a need of reducing the data size in order to match the available bandwidth, large compression techniques can be employed to mitigate this problem. Therefore, a high performance and a low-complexity compression codec is necessary for hyper spectral imagery.The proposed compression scheme achieves lossy compression of hyper spectral images with less mean squared error, based on the discrete cosine transform (DCT) and then coded with SPIHT(Set Partitioning In Hierarchical Trees).
Keywords |
| Hyperspectral images, Discrete Cosine Transform(DCT),Set Partitioning In Hierarchical Trees(SPIHT). |
INTRODUCTION |
| Hyperspectral Images are widely used in a number of civilian and military applications. The images are acquired from plane or satellite borne spectrometers and cover large tracts of the Earth’s surface. Through the analysis of the spectrum of reflected light present in these images, it is possible to identify what materials are present on the land and in the atmosphere. This information has been used for such varied purposes as environmental studies, military surveillance and the analysis and location of mineral deposits. |
| There are number of different sources for hyper spectral images. The most commonly available are probably those from AVIRIS, an instrument which has been flown by NASA over much of the US, CANADA and EUROPE. Images collected by AVIRIS are quite large, with approximately 140 MB of data for every 10 km of flight or about 16 GB for a day’s work (AVIRIS online). The Hyperion imager carried on the EO-1 (Earth Observing-1) satellite is also a common source of hyperspectral data. Image compression is important for this application, where the images must be compressed and sent over a limited bandwidth carrier before analysis can take place. In earlier days scientific data have been mostly compressed by means of lossless methods in order to preserve original data. But now, there has been an increasing interest in their lossy compression. The recent satellites SPOT 4 and IKONOS employ on – board lossy compression prior to down linking the data to ground stations. |
| The proposed scheme has the advantages of low memory space, less computation time and low complexity. In lossy compression, the reconstructed image must be as similar as possible to the original at a target bit rate, typically in mean squared error sense. By increasing the compression ratio, the memory requirements for processing hyper spectral images is reduced. |
| The calculation load of lossy DCT domain is much less that of DWT, so the complexity is lower than other wavelet based schemes[2],[3],[9],[14]. The wavelet-based progressive transmission of image coding, SPIHT achieves a high degree of embedding and compression efficiency[7],[11]. |
II. PROPOSED METHODOLOGY |
| SPIHT BASED DCT COMPRESSION: Many transform coding systems are based on the DCT, which provides a good compromise between information packing ability and computational complexity. In fact, the properties of the DCT have proved to be such practical value that the DCT has became an international standard for transform coding systems. Compared to the other transforms, DCT requires only the fewest coefficients to packing the most information in a single integrated circuit and the boundaries between sub images become visible. |
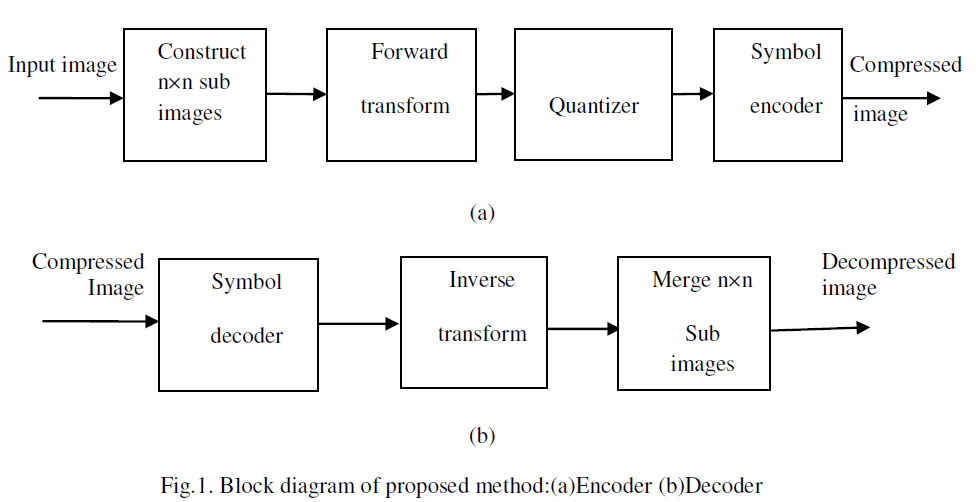 |
| Transform-based compression techniques for hyperspectral images always consist of transforms and zero-tree coding. The basic of this techniques is to exploit spectral and spatial redundancies using decorrelating DCT transforms, and to encode the transformed images using SPIHT coding. For progressive transmission the compressed or coded data can be embedded[5]. The embedded information can be truncated at any point and reconstruct the data to available resolution. The SPIHT has many attractive properties. It is an efficient embedded technique. The encoder and decoder of optimal transform-based compression technique as shown in fig.1. |
| DCT does not directly reduce the number of bits required to represent the block. In fact for an 8×8 block of 8 bit pixels, the DCT produces an 8×8 of 11 bit coefficients (the range of coefficient values is larger than the range of pixel values.) The reduction in the number of bits followed from the observation that, the distribution of coefficients are nonuniform. The low frequency coefficients are concentrate by the DCT transforms and remaining other coefficients are mainly zero. The bit rate reduction is achieved by transmitting the near zero coefficients and by quantizing and coding the remaining coefficients as described below. The spatial redundancy present in the original image block due to the non-uniform coefficient distribution. The DCT transforms a block of pixel values (or residual values) into a set of “spatial frequency “coefficients. The 2D-DCT is particularly good at “compacting” the energy in the block of values by a small number of coefficients. This in turns a reduction in number of coefficients represents the copy of the input image block of pixels. |
| SPIHT ALGORITHM: The SPIHT algorithm improves upon the zero tree concept by replacing the raster scan with a number of sorted list that contain sets of coefficients (ie., zero trees) and individual coefficients. These lists are List of Insignificant Pixels (LIP), List of Insignificant Sets (LIS) and List of Significant Pixels (LSP). |
| Steps of the SPIHT algorithm as follows: |
| 1. LIP,LIS and LSP are initialized and the maximum threshold is determined. |
| 2. In the significant pass of the SPIHT algorithm the List of Insignificant Sets (LIS) is examined in regard to the current threshold. With respect to the current threshold the set in the lists are then partitioned into one or more smaller zero tree sets. |
| 3. Isolated insignificant coefficients are appended to the List of Insignificant Pixels (LIP), while significant coefficients are appended to the List of Significant Pixels (LSP). |
| 4. The LIP is also examined and as coefficient become significant with respect to the current threshold, they are appended to the LSP. |
| 5. Binary symbols are encoded to describe motion of sets and coefficients between the three list. |
| 6. Since the list remained implicitly sorted in an importance ordering, SPIHT achieves a high degree of embedding and compression efficiency. |
| 7. For the next scan, threshold is fixed as T/2 and n is n-1 and repeat steps 3,4 and 5,until the threshold values or bit rate compliance encoder requirements. |
III. EXPERIMENTAL RESULTS |
| The experiments were carried out in a MATLAB Image Processing tool version MATLAB 7.14 R 2012 a and the results were displayed through the Graphical User Interface like fig. 2. Few downloaded hyperspectral images produced by the IKONOS satellite were used in the performance evaluation. |
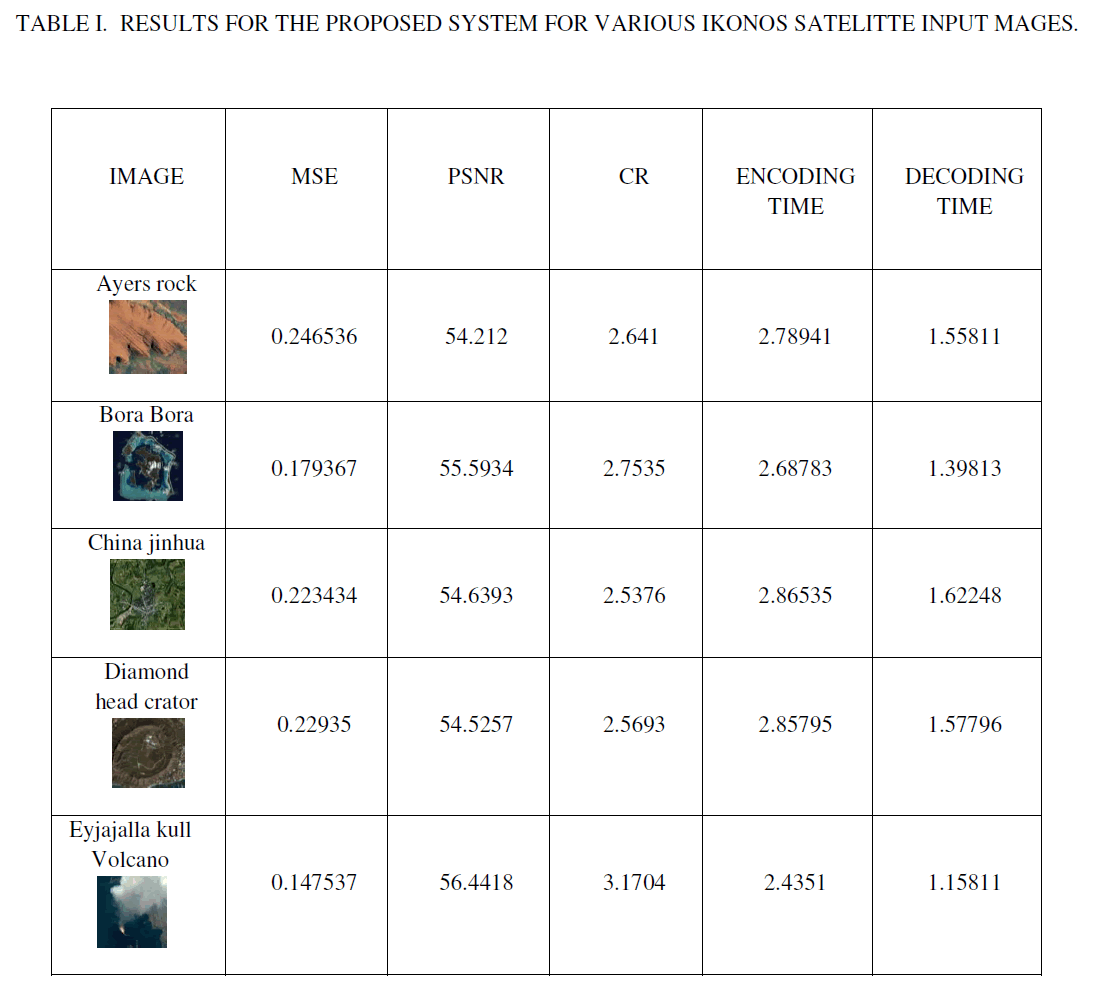
| The computed values such as Compression ratio, MSE, PSNR, encoding time and decoding time corresponding to each input image are tabulated in the Table-I, for various IKONOS satellite input images at higher bit rate. |
 |
 |
V. PERFORMANCE MEASURES |
| Traditionally, performance for lossy compression is determined by simultaneously measuring both distortion and rate. Distortion measures the fidelity of the reconstructed data is the original data, while rate originally measures the amount of compression incurred. |
| i)Distortion: Distortion is commonly measured via a peak signal-to-noise ratio (PSNR) between the original and reconstructed data. Let c[x1, x2] be an N1×N2 hyperspectral data set with variance of . Let c’[x1, x2] be the data set as constructed from the compressed bit stream. |
 |
| MSE- mean squared error between the original image and reconstructed image. |
 |
| v) Computation Time: Time complexity- A measure of the amount of time required to execute an algorithm |
| Factors that should not affect time complexity analysis: |
| ïÃâ÷ The programming language chosen o implement the algorithm |
| ïÃâ÷ The quality of the compiler |
| ïÃâ÷ The speed of the computer on which an algorithm tobe executed |
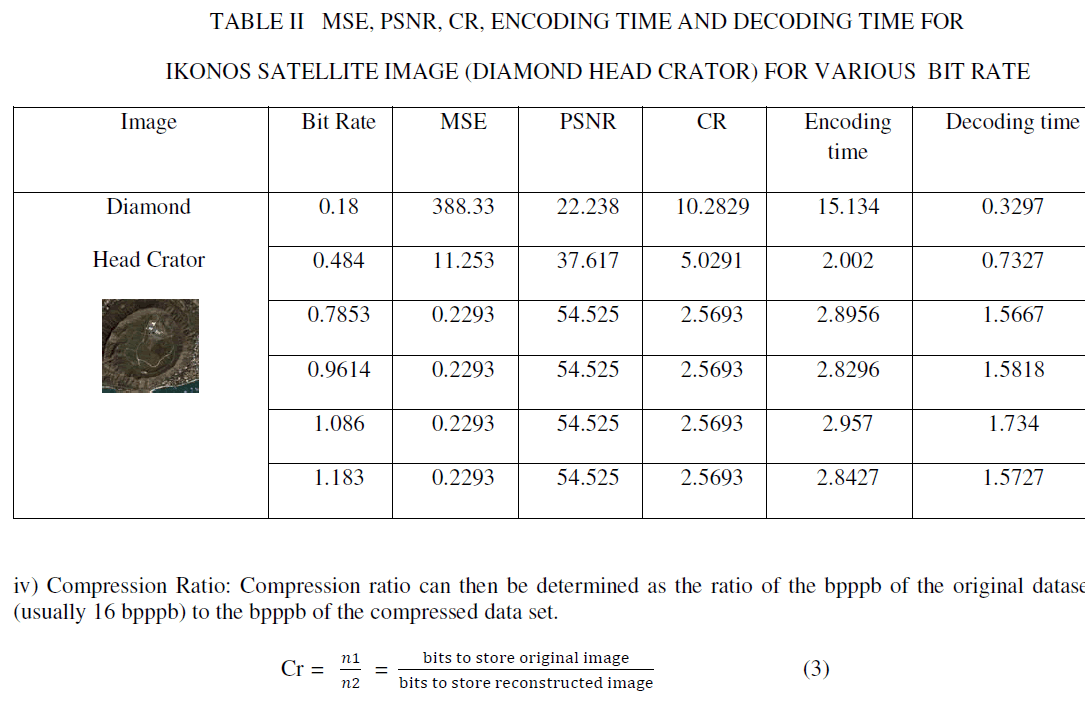
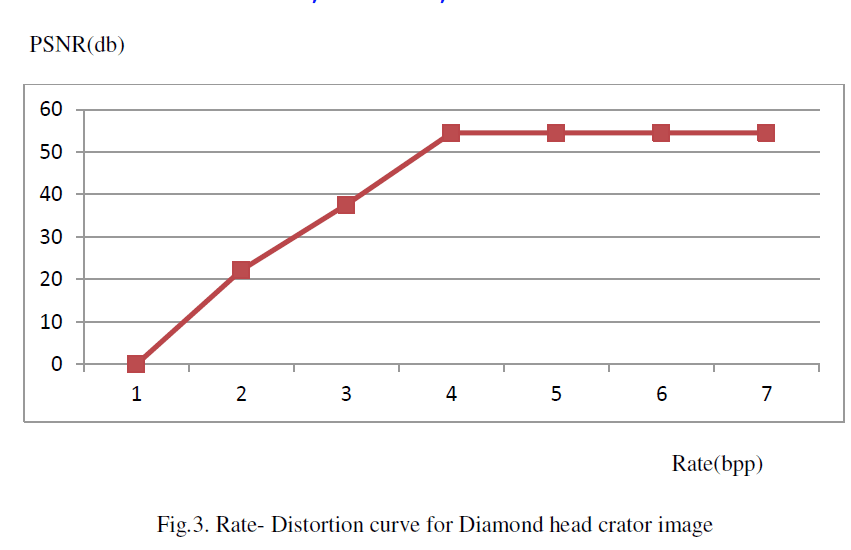
| vi) Rate-distortion: From the tabulated experimental results through Table II , the rate-distortion graph is drawn like as shown in Fig.3. The rate- distortion graphs illustrate the results, as the proposed algorithm achieves very worse ratedistortion performance at low bit rate and becomes very good at moderate and higher bit rate. |
 |
V. CONCLUSION |
| DCT and SPIHT based compression achieves a high degree of embedding and compression efficiency. The proposed scheme also has the advantages, low memory requirements, easy maintenance, and providing security, lower bandwidth for transmission and economic. |
ACKNOWLEDGEMENT |
| The authors would like to thank the anonymous reviewers and the editors who helped to improve the quality of this letter. |
References |
|