International Journal of Innovative Research in Science, Engineering and Technology
MenuISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
| K.Murugan* Assistant Professor, Department of Mathematics, The M.D.T. Hindu College, Tirunelveli, Tamilnadu, India |
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
A ð‘Â. ð‘ž graph G = ð‘‰, ð¸ is said to be a square graceful graph ifthere exists an injective function f: V ðº → 0,1,2,3, … , ð‘ž2 such that the induced mapping ð‘“ð‘ : E ðº → 1,4,9, … , ð‘ž2 defined by ð‘“ð‘ ð‘¢ð‘£ = ð‘“ ð‘¢ − ð‘“ ð‘£ is an injection. The function f is called a square graceful labeling of G. In this paper the square graceful labeling of the caterpillar S ð‘‹1, ð‘‹2, … , ð‘‹ð‘› , the graphs ð‘ƒð‘› −1 1,2, … ð‘› ,mð¾1,ð‘› ∪ ð‘ ð¾1,ð‘¡ , ð¾1,ð‘– , ð‘›ð‘– =1 ð‘ƒð‘› ⨀ð¾1 − ð‘’,H graph and some other graphsare studied. A new parameter called star square graceful deficiency number of a graph is defined and the star square graceful deficiency number of the cycle ð¶3 is determined. Two new definitions namely, odd square graceful labeling and even square graceful labeling of a graph are defined with example.
Keywords |
| Square graceful graph, odd square graceful graph, even square graceful graph, Star square graceful deficiency number of a graph |
INTRODUCTION |
| The graphs considered in this paper are finite, undirected and without loops or multiple edges. Let G = (V, E) be a graph with p vertices and q edges. Terms not defined here are used in the sense of Harary[2].For number theoretic terminology [1] is followed |
| A graph labeling is an assignment of integers to the vertices or edges or both subject to certain conditions. If the domain of the mapping is the set of vertices (edges / both) then the labeling is called a vertex (edge / Total) labeling. There are several types of graph labeling and a detailed survey is found in [4]. |
| Rosa [6] introduced ïÿýïÿý -valuation of a graph and Golomb [5] called it as graceful labeling. Several authors worked on graceful labeling, odd graceful labeling, even graceful labeling, super graceful labeling and skolem –graceful labeling. |
| Recently the concept of square graceful labeling was introduced by T.Tharmaraj and P.B.Sarasija inthe year 2014.They studied the square graceful labeling of various graphs in [7, 8]. |
| The following definitions are necessary for the present study. |
| 1.1 Definition |
| The path on n vertices is denoted byïÿýïÿýïÿýïÿý . |
| Definition [8] |
| A complete bipartite graphïÿýïÿý1,ïÿýïÿý is called a star and it has n +1 vertices and n edges |
| Definition |
| The Corona ïÿýïÿý1 âÃÅ Ã⢠ïÿýïÿý2 of two graphs ïÿýïÿý1 and ïÿýïÿý2 is defined as the graph G by taking one copy of ïÿýïÿý1(which has ïÿýïÿý1 points) and ïÿýïÿý1copies of ïÿýïÿý2 and then joining the ith point of ïÿýïÿý1 to every point in the ith copy of ïÿýïÿý2. |
Definition |
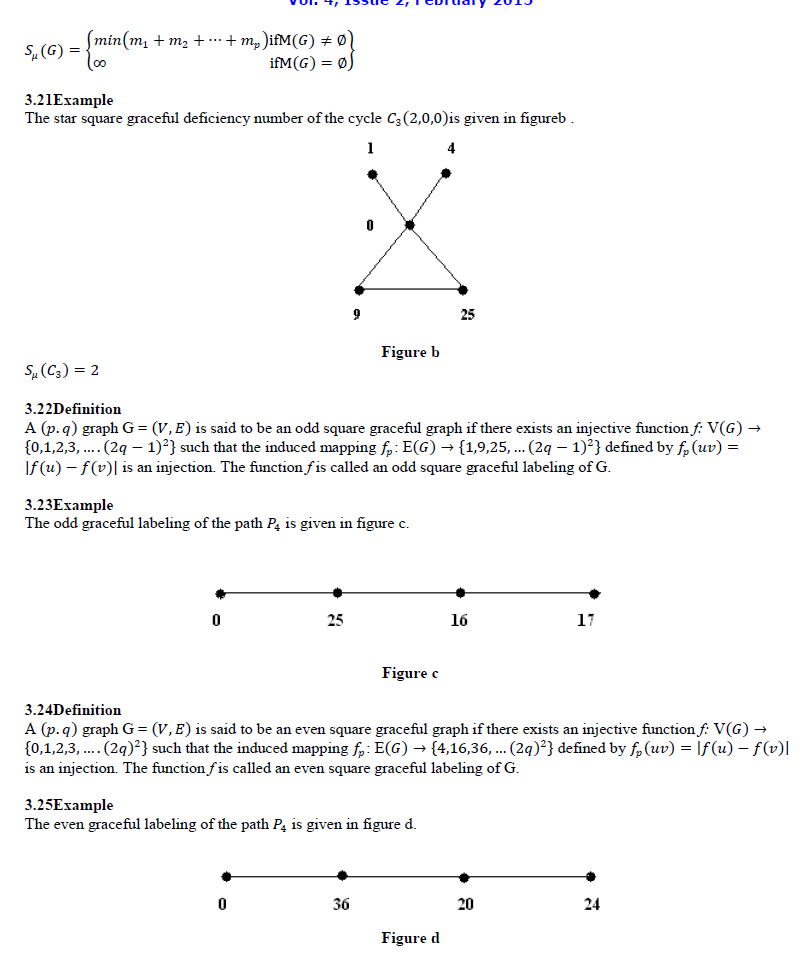
| Let the graphs ïÿýïÿý1 and ïÿýïÿý2 have disjoint vertex sets ïÿýïÿý1 and ïÿýïÿý2 and edge sets ïÿýïÿý1 and ïÿýïÿý2 respectively. Then their union G= ïÿýïÿý1 ∪ ïÿýïÿý2 is a graph with vertex set V= ïÿýïÿý1 ∪ ïÿýïÿý2 and edge set E= ïÿýïÿý1 ∪ ïÿýïÿý2.Clearly ïÿýïÿý1 ∪ ïÿýïÿý2 has ïÿýïÿý1 + ïÿýïÿý2 vertices and ïÿýïÿý1 + ïÿýïÿý2 edges. |
| Definition |
| The graphïÿýïÿýïÿýïÿý@ïÿýïÿýïÿýïÿý is obtained from ïÿýïÿýïÿýïÿý and m copies of ïÿýïÿýïÿýïÿý by identifying one pendant vertex of the ïÿýïÿýïÿýïÿýâÃâÃŽ copy of ïÿýïÿýïÿýïÿý with ïÿýïÿýïÿýïÿýâÃâÃŽ vertex of ïÿýïÿýïÿýïÿý where ïÿýïÿýïÿýïÿý is a path of length m-1. |
SQUARE GRACEFUL GRAPHS |
Definition[7] |
| A ïÿýïÿý. ïÿýïÿý graph G = ïÿýïÿý, ïÿýïÿý is said to be a square graceful graph if there exists an injective function f: V ïÿýïÿý → 0,1,2,3, … , ïÿýïÿý2 such that the induced mapping ïÿýïÿýïÿýïÿý : E ïÿýïÿý → 1,4,9, … , ïÿýïÿý2 defined by ïÿýïÿýïÿýïÿý ïÿýïÿýïÿýïÿý = ïÿýïÿý ïÿýïÿý − ïÿýïÿý ïÿýïÿý is an injection. The function f is called a square graceful labeling of G. |
Example |
| The square graceful labeling of the kite graph is given in figure a |
 |
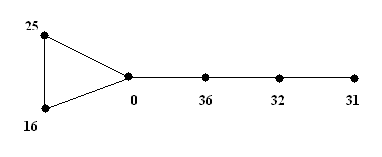| Figure a |
| 2.3 Observation |
| The cycles ïÿýïÿý3 and ïÿýïÿý4 are not square graceful graphs |
 |
 |
 |
 |
 |
 |
 |
 |
CONCLUSION |
| In this paper, the square graceful labeling of some graphs is studied. Examples of some non-square graceful graphs are observed. Star square graceful deficiency number of a graph is determined and the Star square graceful deficiency number of the cycle ïÿýïÿý3 is determined. Odd square graceful labeling and even square graceful labeling are introduced. |
SCOPE FOR FURTHER STUDY |
| The Star square graceful deficiency number of the cycle ïÿýïÿýïÿýïÿýwhere n> 3, the wheel ïÿýïÿýïÿýïÿý , where n> 3,Odd square graceful labeling and even square graceful labeling of various graphs maybe studied. |
ACKNOWLEDGEMENTS |
| The author is thankful to the anonymous Reviewer for the valuable comments and suggestions |
References |
|