ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
T.Nandhini1, A.Kalaichelvi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
In this paper a new class of soft sets called Soft Regular Weakly Closed sets (briefly SRW-Closed sets) in soft topological spaces is introduced and studied. This new class is defined over an initial universe and with a fixed set of parameters. Some basic properties of this new class of soft sets are investigated. This new class of SRW-Closed sets contributes to widening the scope of Soft Topological Spaces and its applications.
Keywords |
| Soft Sets, Soft Topological Spaces, W-closed sets, SW-closed sets, RW-closed sets, SRW-closed sets |
INTRODUCTION |
| Any Research work should result in addition to the existing knowledge of a particular concept. Such an effort not only widens the scope of the concept but also encourages others to explore new and newer ideas. Here the researchers have succeeded in their knowledge building effort by introducing a new class of soft sets called Soft Regular Weakly Closed sets (briefly SRW-Closed sets) in Soft Topological Spaces. |
| Molodtsov (1999) initiated the theory of soft sets as a new mathematical tool for dealing uncertainty, which is completely a new approach for modeling vagueness and uncertainties. Soft Set Theory has a rich potential for application in solving practical problems in Economics, Social Sciences, Medical Sciences etc. Applications of Soft Set Theory in other disciplines and in real life problems are now catching momentum. Molodtsov successfully applied Soft Theory into several directions, such as Smoothness of Functions, Game theory, Operations Research, Riemann Integration, Perron Integration, Theory of Probability, Theory of Measurement and so on. Maji et al. (2002) gave first practical application of Soft Sets in decision making problems. Shabir and Naz(2011) introduce the notion of soft topological spaces which are defined over an initial universe with a fixed set of parameters. They studied some basic concepts of soft topological spaces also some related concepts such as soft interior, soft closure, soft subspace and soft separation axioms. . In this paper a new class of sets called Soft Regular Weakly Closed sets (SRW-Closed sets) are introduced and few of their properties are investigated. |
RELATED WORK |
| Some concepts in mathematics can be considered as mathematical tool for dealing with uncertainties namely theory of vague sets, theory of rough sets and etc. But all of these theories have their all difficulties. The concept of soft set now introduce by Molodtsov[10] in 1999 as a general mathematical tool for modeling uncertainty present in real life. Later on Maji et al [9] proposed several operations on soft sets and some basic properties and then Pei and Miao [12] investigated the relationships between soft sets and information systems. Shabir and Naz [12] introduced the notion of soft topological spaces which are defined over an initial universe with a fixed set of parameters. Latter on Benchalli and Wali [3] introduced RW-Closed sets in Topological Spaces. |
PRELIMINARIES |
| Let X be an initial universe set and E be the set of parameters. Let P(X) denote the power set of X. |
| Definition 2.1[10] |
| For A ⊆ E, the pair (F,A) is called a Soft Set over X, where Fis a mapping given by F:A → P(X). |
| In other words, a soft set over X is a parameterized family of subsets of the universeX. For ε ∈ A, F(ε) may be considered as the set of ε- approximate elements of the soft set (F,A). |
| Definition 2.2 [11] |
| A soft set (F,A) over X is said to be Null Soft Set denoted by Φ if for all e ∈ A, F(e) = φ. A soft set (F,E) over Xis said to be an Absolute Soft Set denoted by A if for all e ∈ A,F(e) = X. |
| Definition 2.3 [9] |
| The Union of two soft sets(F, A) and (G, B)over X is the soft set (H, C), where C = A ∪ B, and for all e ∈ C, H(e) = F(e), if e ∈ A\B, H(e) = G(e) if e ∈ B\A andH(e) = F(e) ∪ G(e)if e ∈ A ∩ B and is denoted as (F, A) ∪ (G, B) = (H, C). |
| Definition 2.4 [9] |
| The Intersection of two soft sets (F, A) and (G, B)over X is the soft set (H,C), whereC = A ∩ B and H(e) = F(e) ∩ G(e)for all e ∈ C and is denoted as(F, A) ∩ (G,B) = (H, C). |
| Definition 2.5 [11] |
| The Relative Complement of (F,A) is denoted by (F, A)c and is defined by (F,A)c = (Fc,A) where Fc:A → P(X) is a mapping given by Fc(e) = X − F(e) for all e ∈ A. |
| Definition 2.6 [11] |
| The Difference(H, E) of two soft sets (F, E) and (G, E)over X, denoted by (F, E)\(G,E) is defined as H(e) = F(e)\G(e) for all e ∈ E. |
| Definition 2.7 [11] |
| Let (F,A) and (G, B) be soft sets over X, we say that (F,A) is a Soft Subset of (G,B) if A ⊆ B and for all e ∈ A, F(e)and G(e) are identical approximations. We write (F, A) ⊆ (G, B). |
| Definition 2.8 [11] |
| Let τ be a collection of soft sets over X with the fixed set E of parameters. Then τ is called a Soft Topology onX if |
| i. Φ,E belongs to τ |
| ii. The union of any number of soft sets in τ belongs to τ. |
| iii. The intersection of any two soft sets in τ belongs to τ. |
| The triplet (X, τ,E) is called Soft Topological Spaces over X. |
| The members of τ are called Soft Open sets in X and complements of them are called Soft Closed sets inX. |
| Definition 2.9 [11] |
| Let (X, τ,E) be a Soft Topological Spaces overX. The Soft Interior of (F, E) denoted by Int(F, E) is the union of all soft open subsets of (F,E). Clearly (F, E) is the largest soft open set over X which is contained in (F, E). The Soft Closure of (F, E) denoted by Cl(F,E) is the intersection of closed sets containing (F, E). Clearly (F, E) is the smallest soft closed set containing (F,E). |
| Int(F, E) =∪ {(O.E): (O, E)is soft open and (O,E) ⊆ (F,E)} |
| Cl(F,E) =∪ {(O. E): (O, E)is soft closed and (F, E) ⊆ (O,E)} |
| Result2.10 [11] |
| Let (X, τ,E) be a Soft Topological Spaces over X and (F, E) and (G, E) be a soft sets over X. Then |
| i. (F, E) is soft closed set if and only if (F,E) = Cl(F,E) |
| ii. Cl((F, E) ∪ (G, E)) = Cl(F,E) ∪ Cl(G,E) |
| iii. Cl(Cl(F, E)) = Cl(F, E). |
| Definition 2.11[11] |
| In a Soft Topological Spaces (X, τ, E), a soft set (F, E)over X is called |
| i. a Soft Semi Open if (F, E) ⊆ Cl(Int(F, E)) and Soft Semi Closed if Int(Cl(F, E)) ⊆ (F, E). |
| ii. a Soft Regular Open if (F, E) = Int(Cl(F, E)) and Soft Regular Closed if (F, E) = Cl(Int(F, E)). |
| iii. a Soft Weakly Closed(briefly SW-Closed) if Cl((F,E) ⊆ (U, E) whenever (F,E) ⊆ (U, E) and (U, E) is soft semi open in X. |
| iv. a Soft Regular Semi Open if there exists a soft regular open set (U, E) such that (U, E) ⊆ (F, E) ⊆ Cl(U, E). |
| Result 2.12[11] |
| i. Every soft regular semi open set in (X, τ,E) is soft semi open. |
| ii. If (F, E) is soft regular semi open in (X, τ,E) then (X, E)\(F, E) is also soft regular semi open. |
| Definition 2.13 [3] |
| A subset A of a Topological Spaces (X, τ) is called |
| i. A Semi Open if A ⊆ Cl(Int(A)) and Semi Closed if Int(Cl(A) ⊆ A. |
| ii. a Regular Open if A = Int(Cl(A)) and Regular Closed if A = Cl(Int(A)). |
| iii. a Regular Semi Open if there exists a regular open set U such that U ⊆ A ⊆ Cl(U). |
| iv. a Weakly Closed (briefly W-Closed) ifCl(A) ⊆ U whenever A ⊆ U and U is semi open in X. |
| v. a Regular Weakly Closed(briefly RW-Closed) if Cl(A) ⊆ U whenever A ⊆ U and U is regular semi open in (X, τ). |
SRW-CLOSED SETS IN SOFT TOPOLOGICAL SPACES |
| Definition 3.1 |
| Let (X, τ,E) be a Soft Topological Spaces. A soft set (F, E) is called Soft Regular Weakly Closed (briefly SRWClosed) ifCl(F, E) ⊆ (U,E) whenever (F, E) ⊆ (U, E) and (U,E) is soft regular semi open in(X, τ,E). |
| Example 3.2 |
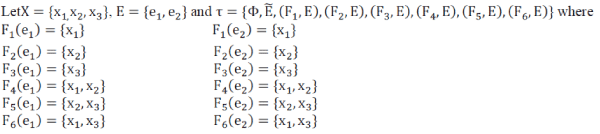 |
| Then (X, τ,E) is a Soft Topological Spaces. Define soft sets (G, E) and (H, E) over X such that |
| Here both (G, E) and (H, E) are SRW-Closed sets in(X, τ,E). |
| Theorem 3.3 |
| Every soft closed set is a SRW-Closed set but not conversely. |
| Proof |
| Let (F, E) be a soft closed set in (X, τ, E) and (U,E) be soft regular semi open set such that(F,E) ⊆ (U,E). Consider Cl(F, E) = (F, E) ⊆ (U, E). Therefore (F, E)is SRW-Closed set. |
| In Example3.2, (G,E) is a SRW-Closed set but not soft closed set. |
| Theorem 3.4 |
| Every SW-Closed set is a SRW-Closed set but not conversely. |
| Proof |
| The proof follows from the definitions and the fact that every soft regular semi open set is soft semi open set. In Example3.2, (G,E) is a SRW-Closed set but not SW-Closed set. |
| Theorem 3.5 |
| If (F, E) and (G,E) are SRW-Closed sets in(X, τ,E)then (F, E) ∪ (G, E)is SRW-Closed set in (X, τ,E). |
| Proof |
| Suppose (F, E) and (G,E) are SRW-Closed sets in (X, τ,E). Then Cl(F,E) ⊆ (U,E) and Cl(G,E) ⊆ (U, E) where (F, E) ⊆ (U,E)and (G, E) ⊆ (U, E). |
| Hence Cl(F,E) ∪ (G,E) = Cl(F, E) ∪ Cl(G, E) ⊆ (U,E). That is Cl(F, E) ∪ (G, E) ⊆ (U, E). Therefore (F, E) ∪ (G, E) is SRW-Closed set in(X, τ,E). |
| Remark 3.6 |
| Intersection of two SRW Closed sets need not be a SRW-Closed set. |
| In Example 3.2,(H, E) and (G,E) are SRW-Closed sets in (X, τ,E). But (H, E) ∩ (G, E) is not SRW-Closed set in (X, τ,E). |
| Theorem 3.7 |
| If a soft set (F,E)is SRW-Closed set in (X, τ, E) then the difference Cl(F, E)\(F,E) does not contain any nonempty soft regular semi open set in (X, τ, E). |
| Proof |
| We prove the result by contradiction. Let (U,E)be a non-empty soft regular semi open set such that Therefore (U,E) ⊆ (X,E)\(F,E) then (F, E) ⊆ (X, E)\(U,E). Since (U,E) is soft regular semi open set by result 2.12(ii) (X, E)\(U,E) is also soft regular semi open set in (X, τ, E). Since (F,E) is SRW-Closed set in (X, τ,E)andCl(F, E) ⊆ (X, E)\(U,E), so (U, E) ⊆ (X, E)\Cl(F, E). Also by (1)(U,E) ⊆ Cl(F,E). Therefore (U,E) ⊆ Cl(F, E) ∩(X, E)\Cl(F, E) = φ.This shows that (U,E) is empty, which is a contradiction. |
| Hence Cl(F, E)\(F, E) does not contain any non-empty soft regular semi open set in (X, τ,E). |
| Corollary 3.8 |
| If (F, E) is SRW-Closed set in (X, τ,E) then Cl(F,E)\(F,E) does not contain any non-empty soft regular open set in (X, τ, E). |
| Proof |
| Follows from theorem (3.9) and the fact that every soft regular open set is soft regular semi open set. |
| Corollary 3.9 |
| If (F, E) is SRW-Closed set in (X, τ,E) then Cl(F, E)\(F,E) does not contain any non-empty soft regular closed set in(X, τ,E). |
| Proof |
| Follows from theorem (3.9) and the fact that every soft regular open set is soft regular semi open set. |
| Theorem 3.10 |
| If (F,E) is a SRW-Closed set in (X, τ,E) such that (F, E) ⊆ (G, E) ⊆ Cl(F, E) then (G,E) is SRW-Closed set in (X, τ,E). |
| Proof |
| Let (F, E) be SRW-Closed set in (X, τ,E) such that(F, E) ⊆ (G, E) ⊆ Cl(F, E). Let (U,E) be a soft regular semi open set of (X, τ,E) such that (G,E) ⊆ (U, E). Then (F,E) ⊆ (U, E).Since (F, E) is SRW-Closed set,Cl(F, E) ⊆ (U,E).Now Cl(G, E) ⊆ Cl(Cl(F,E)) = Cl(F,E) ⊆ (U,E). That is Cl(G,E) ⊆ (U,E). Therefore (G,E) is SRW-Closed set in(X, τ,E). |
| Theorem 3.11 |
| Let (F,E) is SRW-Closed set in (X, τ,E). Then (F,E) is soft closed set if and only if Cl(F, E)\(F,E) is soft regular semi open set in (X, τ,E). |
| Proof |
| Suppose (F, E) is soft closed set in (X, τ,E). Then Cl(F,E) = (F,E)and Cl(F, E)\(F,E) = φ, which is a soft regular semi open set in (X, τ,E). |
| Conversely, suppose Cl(F,E)\(F,E) is soft regular semi open set in (X, τ,E). Since(F, E) is SRW-Closed set, by theorem (3.7), Cl(F,E)\(F,E) does not contain any nonempty soft regular semi open set in (X, τ,E). Then Cl(F,E)\(F,E) = φ. Hence (F, E) is soft closed set in(X, τ,E). |
CONCLUSION |
| In the present work, a new class of sets called SRW-Closed sets in Soft Topological Spaces is introduced and some of their properties are studied. This new class of sets widens the scope to do further research in the areas like Bitopological Spaces, Smooth topological Spaces and Fuzzy Soft Topological Spaces. |
References |
|