Steady State Extended Kalman Filter
Application for a Heat Exchanger Model

Natarajan.J; Tamilmani.P; Issan Raj.R

Steady State Extended Kalman Filter Application for a Heat Exchanger Model

Natarajan.J, Tamilmani.P, Issan Raj.R

PG Student, Department of Electronics and Instrumentation,Valliammai Engineering College, Chennai, India
Assistant Professor, Department of Electronics and Instrumentation,Valliammai Engineering College,Chennai, India
Assistant Professor, Department of Electronics and Instrumentation,Valliammai Engineering College, Chennai, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering

Abstract

Heat exchanger is a non-linear process and to estimate the parameters, filtering techniques are used. This project deals with Counter-Flow Double pipe heat exchanger. Empirical formulae of heat transfer have been included to estimate the parameters and for modeling. PI controller is used to control and reduce the offset. The Kalman filtering approach has seen many applications such as forecasting, condition monitoring, diagnosis of fault, and process control. The state variables of heat exchanger are obtained in state space model and the states are estimated using extended Kalman filter (EKF). The algorithm of EKF is implemented in MATLAB and it will be compared with the other filtering technique. Finally, the estimated state is compared the true state update. The filters are effective in the estimating the nonlinear process.

Keywords

Heat exchanger, nonlinear, filtering, EKF, estimation, true state update

INTRODUCTION

Heat exchangers are widely used in chemical, power and food processing plants where there is a very of need to control the plant temperatures. It is very essential to monitor and control the plant temperature to maintain the product quality. Heat exchangers are modeled in many ways. To determine the model parameters, geometry of the heat exchanger and the empirical relations of the overall heat transfer coefficient are considered. In literature [1], the study proved that EKF approach is better than system identification techniques. Also, the EKF approach uses optimization of parameters against a score function in math libraries. The state estimation of a dynamic heat exchanger model is considered here. Mathematical model of the counter flow double pipe heat exchanger is made in [2]. Usually to estimate the parameters by state estimation it requires several experimental setup that is quiet challenging and expensive. Implementation of EKF is found in induction motor driver application in numerous configurations [5, 6, 7]. Therefore, the estimation of such parameters by state estimation tends to have a great value.

State estimation technique by Kalman filter is developed in the year 1960.The filtering techniques are widely used in the various field of engineering and scientific applications. Also,the applications include communications, medical field, control, and various emerging fields. In general, Kalman filters are suitable for linear process. Process control is nonlinear and to remove the noise in the nonlinear system, several filtering techniques have been developed. The noise present in the system is electromagnetic in nature. To remove such noise, it is considered as a statistical model and the estimates in it are evaluated in a curve of probabilistic value. The main problem with EKF is the computation of Jacobian matrix of the model. When the system is nonlinear severely, the estimation result leads worst problems. When the system is complex nonlinear, the performance of EKF is not better comparing to its normal operation.

The aim is to estimate the state variables (inlet and outlet temperature) of the heat exchanger model using EKF (Extended Kalman Filter). The power system estimates of PMU model had been done by considering the new state estimation model [3]. In this, the double state estimation model is validated by the simulation. State estimation technique is proved to be more advantageous than the other techniques. This study proves and investigates the version of EKF to implement by considering the inlet and outlet temperatures as state variables. To estimate a process KF based feedback control is used.

II. HEAT EXCHANGER - MODEL

Heat exchangers are the devices used in transferring the heat energy form one fluid to another. The counter-flow double pipe heat exchanger process involves the direct lumping element. The dynamics of the system is obtained by the second order differential equation [1]. From the second order differential equation, state model is obtained by considering the Tho and Tco, the outlet temperature at hot and cold junctions respectively.

We cannot have the description of plant or process to determine the parameters and hence mathematical modeling is performed. Here, the counter-flow double-pipe heat exchanger modeling is done by considering the energy balance equation. The experimental values of the counter-flow double-pipe heat exchanger are substituted from [2].

The namecounter-flow double-pipe heat exchanger arose because of its counter flow of the hot and cold fluids in the junctions of the heat exchanger. The heat exchanger applications vary many in process industries, food processing industries, and chemical industries and so on. The counter-flow double pipe heat exchangers (coolers) are found commonly in chemical processes. In general, the applications where temperature of specific processes needs to get down or in exothermic process.

The accumulation of energy is given by the energy balance equation in [1] and the modeling for the heat exchanger model in [8]: [Flow of moles of gth component into system] – [flow of moles of gth component out of system] + [rate of formation of moles of gth component from chemical reactions] = [time rate of change of moles of gth component inside system]

From the above energy balance equation, the 2nd order differential equation by considering single element per fluid:

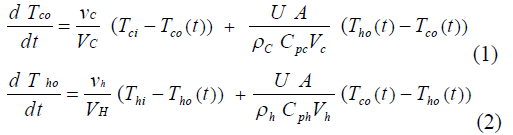The terms in equations are represented in the table 1 and the above equations takes account of the following assumptions:

a1 equals the inflows and outflows and implies constant volume in both tubes;

a2 the heat transfer coefficient relates the flow and heat of the fluids;

a3, no heat transfer between the environment and external tube;

a4 the thermophysical properties in the fluids remains constant;

a5 there is no energy stored in the walls;

a6, inlet temperature is maintained constantly.

The heat exchanger model implemented here is a single cell which has two perfectly stirred tanks with both inflows and outflows. The state variables assumed here has initial values. A low-order model like is proven useful for observer or control which is highly useful for synthesis purposes, where higher-order dynamics is convenient for the implementation of numerical simulations oriented to test the (observer or control) designed algorithms.

III. EXTENDED KALMAN FILTER

State estimation technique is achieved by Kalman filtering. Kalman filters are utilized for linear systems, for nonlinear systems, the Extended Kalman filter is much of interest. In engineering and embedded systems filtering is desirable in many situations. For instance, radio communication signals are corrupted with noise. A good filtering algorithm can remove the noise present in the system. Usually, noise present in the signal is electromagnetic in nature. The tool that can estimate the variables of wide range in a process is termed to be Kalman filters. Rudolf E. Kalman developed this filter in the year 1960. Kalman filters have been subjected as extensive and research oriented application, particularly in tracking and navigation. It is powerful in various aspects, such as tracking the events as past, present, and future states, it performs precisely when the modeled system is unknown. It is theoretically attractive because of all the filters; it minimizes the variance of the estimated error.

The EKF was proposed for nonlinear systems, the state model is obtained by the assumptions of two state variables and the state model is represented as follows:

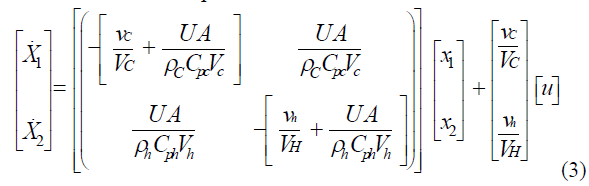The above shown is the state model of the heat exchanger model. Output equation of the model is obtained by the consideration that, outlet temperature at cold junction or the outlet temperature at the hot junction. To control the process, accurate estimate of the process variables are needed. EKF approach is mainly for nonlinear systems, the algorithm contains five and two phases:

EKF time update equations are given below for the prediction phase as follows:

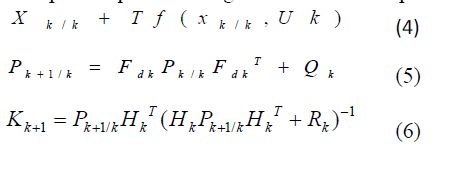The correction phase is represented below,

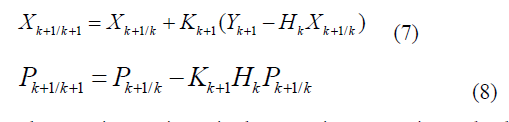K is the Kalman gain matrix, P is the covariance matrix, and Fd is the Jacobian matix of the system. The Jacobian matrix for the output is denoted as H.

IV. SIMULATION RESULTS

The response of the EKF simulation is obtained and it is shown below. It shows that, the noise reduction of the heat exchanger model. Also, there is a presence of noise in the system.

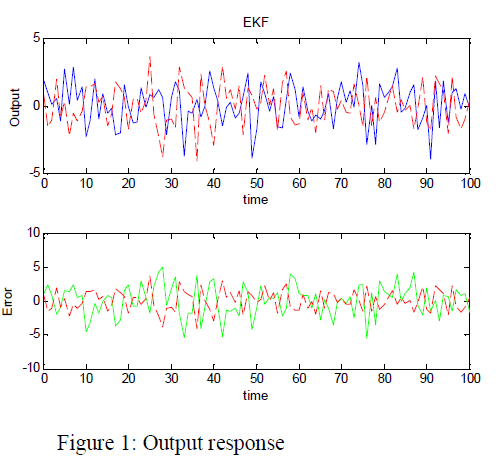CONCLUSION

The state variables estimation of a heat exchanger model is done by extended kalman filter by computing the two phases, prediction and correction. Extended Kalman filter is suitable only for nonlinear processes. The state variables of the counter-flow double-pipe heat exchanger are estimated.

The steady-state EKF algorithm will compares the estimated state with true state. State variable estimation technique is fast. To remove the error in further, Unscented Kalman Filter will be compared. UKF is advantageous and it updates the weight by sigma points for the state variables assumed and reduces the noise comparing with EKF.

References

Arthur G.O. Mutambara and Marwan S.Y. Al-Haik, “EKF based Parameter Estimation for a Heat Exchanger,” Proceedings of the American Control Conference, California.1999
Betty Lopez Zapata, R.F. Escobar, Manuel Adam Medina and Carlos M. Astroga Zaragoza, “State Variables Estimation for a Counter-Flow Double-Piip Heat Exchanger using Multi-linear model”, Electronics, Robotics and Automotive Mechanics Conference 2009.
Hongga Zhoa “A New State Estimation model of utilizing PMU measurements,” Proceedings of the International Conference on Power System technology, 2006.
Fredrik Gustafsson, Fellow, IEEE and Gustaf Hendeby, Member, IEEE “Some Relations between Extended and Unscented Kalman Filters” IEEE TRANSACTIONS ON SIGNAL PROCESSING, VOL. 60, NO. 2, FEBRUARY 2012.
M. Barut, S. Bogosyan, and M. Gokasan, “Speed-sensorless estimation for induction motors using extended kalman filters,” IEEE Trans. Ind. Electronics, Vol. 54, no 1, pp.272-280, Feb 2007
N. Salvatore et. al., “Optimization of delayed-state Kalman filter based algorithm via differential evolution for sensorless control of induction motors,” IEEE Trans. Ind. Electron., vol. 57, no 1, pp. 385-394, Jan 2010.
Y.R. Kim, S.K. Sul, M.H. Park,“Speed sensorless vector control of induction motor using Extended Kalman Filter,” IEEE Trans. Ind. Applic., vol.30, pp.1225-1233, 1994.
Fazlur Rahman MHR, D.R., “Modeling and dynamic feedback linearisation of a heat exchanger model”, proceeding of the third IEEE conference on control applications, 1994: pp. 1801-6.