ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
D. Torres Guzman1, C. S. Carbajal2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
Quasi-periodic signals can be contaminated with random distortions (“artifacts”) not manifested periodically and homogenously,without affecting all signal cycles.These distortions cannot be characterized statistically or modelled with a known probability function. In this paper, a stochastic analysis method to detect the presence of such distortions is proposed. The aim of the method is identifying the affected cycles, which exhibit a different morphology compared to the unaffected cycles.The identification of the affected cycles (or non-homogeneous cycles) allows to estimate parameters and extract the useful information needed for a correct characterization of the signal.The method compares nearly periodic signal cycles through the mean square error and the estimated variance of the inherent noise affecting the signal. Expressions are derived to estimate this error and compared with experimental results.
Keywords |
| Quasi-periodic Signals, Random Distortions,Artifacts, Stochastic Analysis,SignalProcessing, Noise. |
INTRODUCTION |
| Measurement, acquisition and processing of quasi-periodic signals, may be affected by many noise sources. On the one hand, there are noise sources generate distortions, which are always present, can be periodic or exhibit a homogeneous behaviour. They affect all signal cycles and are generally modelled as stochastic processes (Gaussian, Poisson, Markov, etc.) with a known probability function using the principles of statistical independence and ergodicity [1]. These distortions include those due to the following noise sources: instrumentation noise(thermal noise, electrostatic noise, electromagnetic noise, processing noise due to stages of analog to digital conversion, environmental noise and interferences) [1-2], improper usage or improper configuration of technology (incorrect colocation of transducers and sensors, erroneous selections of gains,attenuations, filters cutoff frequencies, offset settings etc.) [2] and noise due to own target application (respiratory motions, motions during cycles of systole and diastole of the heart, patient motions, etc.). These types of noise sources have been extensively studied. The papers describing the state of the art includes plenty of methods and systems to their reduction/attenuation.Some of the methods used to attenuate them and to improve de SNR (Signal to Noise Ratio) are:analog and digital classical filtering techniques (high-pass, low-pass and band-pass), advanced filtering techniques, (optimal and adaptive filtering), time-scale and time-frequency transformations, neural networks, averaging techniques, higher order statistics, fuzzy logic, spectral subtraction, linear prediction, Bayesian estimation and many others.For the purposes of this paper, all these noise sources with the above characteristics will be called inherent noise. |
| On the other hand, there are other type of noise sources that produce distortions that are not manifested periodically and homogenously, not affecting all signal cycles.For example: the presence of emboli generates a distortion that will not be distributed at all cycles of the blood flowsignal, the presence of certain cardiac events did not affect all cycles of electrocardiography (ECG) signal, etc.These distortions cannot be characterized statistically or modelled with a known probability function.Such distortions can generate larger deformations to a given segment of the signal, producing a total loss of its morphology, misleading the characterization of the signal under analysis. So, the identification or detection of these types of distortion constitutes one of the most principal challenges in signal processing [3]. |
| The aim of this paper is to propose a method for identifying the cycles of the studied signal which have a different morphology from the rest.In other words, identify those cycles, which, besides being affected by the inherent noise, are affected by distortions that occur on a “casual manner”. |
II.RELATED WORK |
| One of the most widely used techniques for identifying non-repetitive and/or periodic patterns or distortions has been the wavelet transform [4-5].This technique adapts a wavelet pattern to the characteristics of the signal distortion to be identified.This has been used for identification of epileptic spikes in electroencephalography (EEG) signal [6-9], to identify emboli in the blood flow signal [10-13], to identify arrhythmias in the ECG signal [14-16], for identifying flaws in industrial materials (metals, concrete, etc.)in the ultrasound signal [17-19], and many other scenarios. |
| The main disadvantage of detection methods based on wavelet is that they depends on the shape and characteristics of pattern to be identified [5], which is not always possible in many real applications.For example, during the verification of a graft, in coronary revascularization procedure, a motion between the ultrasound transducer and the surface (blood vessel 2 to 4 mm in diameter) may cause, in the current acquired cycle, a distortion whose shape is unknown.This distortion may eventually affect one or more signal cycles, and can show different morphology in the affected cycles.This dependence constitutes a limitation for the methods based on wavelets in real-time applications. |
| The method, in this paper, does not needto identify the distortion characteristics (amplitude, frequency, power, duration, etc.).Indeed, it is independent of the characteristics of the particular application and of the signal carrying useful information [3]. |
III.PROPOSED METHODOLOGY AND DISCUSSION |
A.Quasi-periodic signals and noise sources |
 |
 |
C. Noise power estimation |
| For the identification of the cycles, which are affected by the noise ïÿýïÿýïÿýïÿý , is necessary to find the detectionthresholdïÿýïÿýïÿýïÿý ïÿýïÿý as shown in (10). For this, is necessary to estimate the variance of the noise sources ïÿýïÿýïÿýïÿý . Due to the own characteristics of this kind of noise, a good method for achieve that is by using the wavelet decomposition. This method have been extensively used for denoising in many scenarios. In [20-21] the authors demonstrated that the first level decomposition of a signal using wavelet is enough to obtain a good approximation of the noise level in this signal. The noise level is estimated by the direct relationship between the absolute value of the mean of the detail coefficients and the factor 0.6745. |
D. Selecting the parameter |
| For the purposes of this paper, the selection of parameter ïÿýïÿý is not considered crucial. Therefore, the implemented techniques for the selection and adjustment of this parameter will not be exposed here [3]. Furthermore, the values used for ïÿýïÿý were selected empirically. |
IV. EXPERIMENTAL RESULTS AND DISCUSSION |
Simulations |
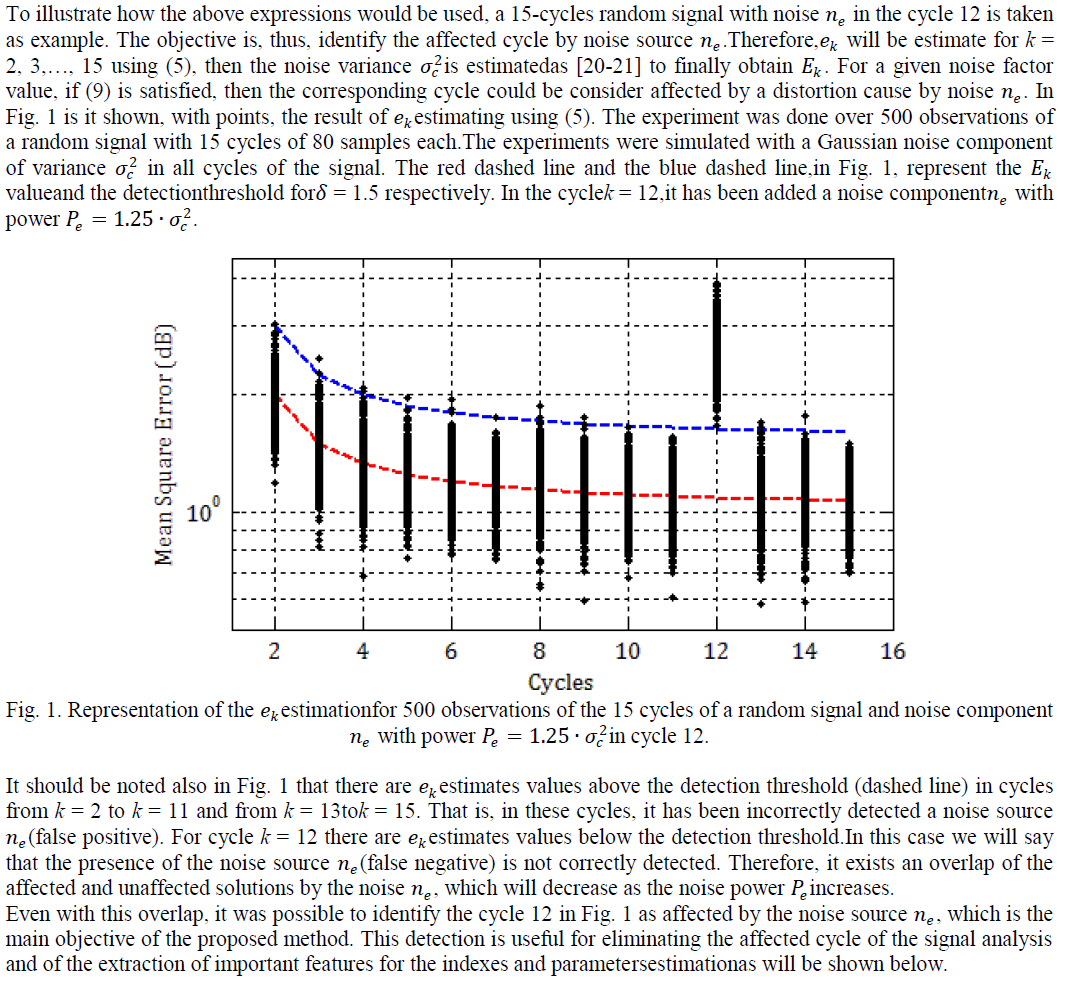 |
Real applications |
| Blood flow signal |
| The method is applicable over any quasi-periodic signal. Fig.2 shows the envelope of maximum frequencies (normalized with respect to its maximum value) of a Doppler blood flow signal sampled at 11.025kHz. |
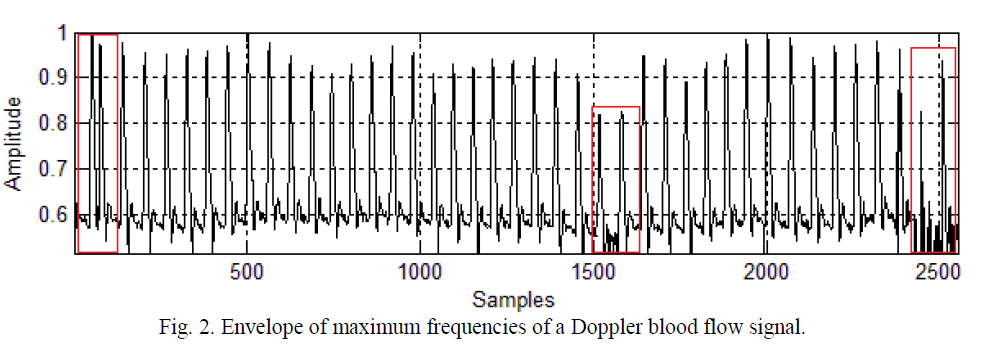 |
| As it can be seen in Fig. 2, there are segments (one or more cycles marked with red rectangles) of the blood flow signal exhibiting a completely different morphology from the rest and they are severely distorted. Affected cycles do not contain clinically useful information. It should be noted that these distortions are not periodic, and they not affect the entire signal (all cycles), therefore we can say that are generated by a noise sourceïÿýïÿýïÿýïÿý .The goal is, then, to identify the cycles corresponding to these signal segments. This will allow exclude them of the signal analysisand estimate the clinical indexes needed for a correct diagnosissafely. |
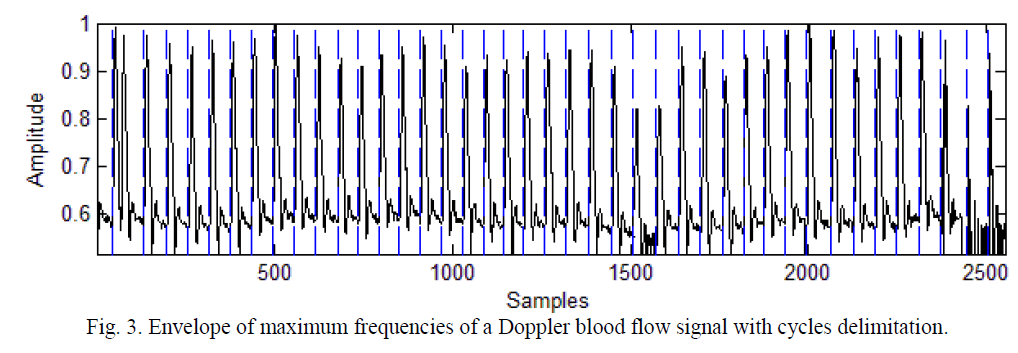
| For the application of the method, the first step is the delimitation of the signal cycles as indicated by [22]. This is necessary to average the cycles and then estimatethe mean square error between them, as shown in (5). Fig. 3 shows the result of this operation,where the blue vertical dashed lines delimit the signal cycles to a length equal to that of a cardiac cycle. |
 |
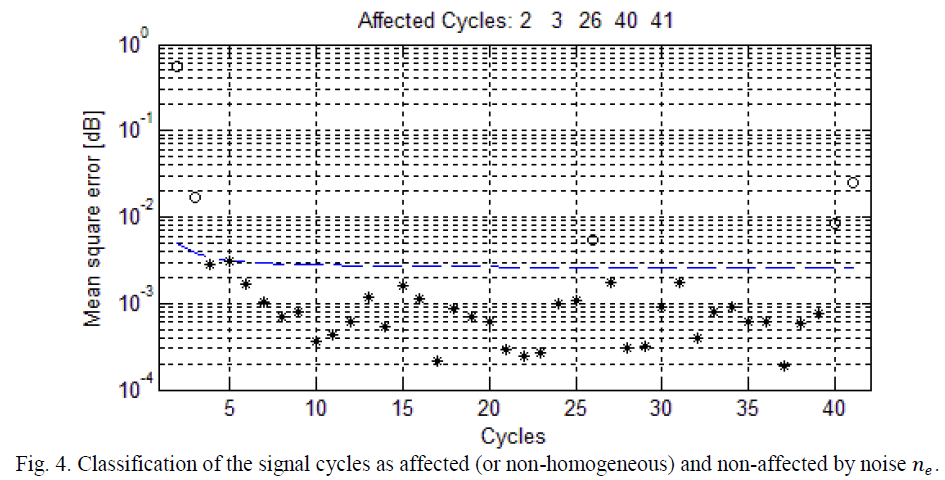
| Once the cycles has been delimited, the noise varianceis estimated, using wavelet decomposition. Then, a real value (greater than zero) for the parameter ïÿýïÿý[3] is proposed and the detection threshold is determined using (10). Finally it is possible identify the no-homogeneous cycles of the analyzed signal estimating the mean square error for each cycle and comparing it with the detection threshold, using (9). The result of all of these operations is shown in Fig. 4. |
| In Fig.4 the cycles detected as affected by any noise source ïÿýïÿýïÿýïÿý , are marked with circles and the cycles detected as nonaffected are marked with asterisks. The blue dashed line represents the detectionthreshold. It should be noted that, cycles detected as affected match the cycles of the signal shown in Fig. 2 which exhibited a different behavior from the rest. |
 |
| For a better appreciation of the difference between the cycles classified as affected and unaffected in Fig. 4, the Fig. 5 shows, with the blue line, the final average cycle obtained with the proposed method and two set of cycles; in 5.a the cycles identified as affected (or non-homogeneous cycles) and 5.b the cycles identified as non-affected. |
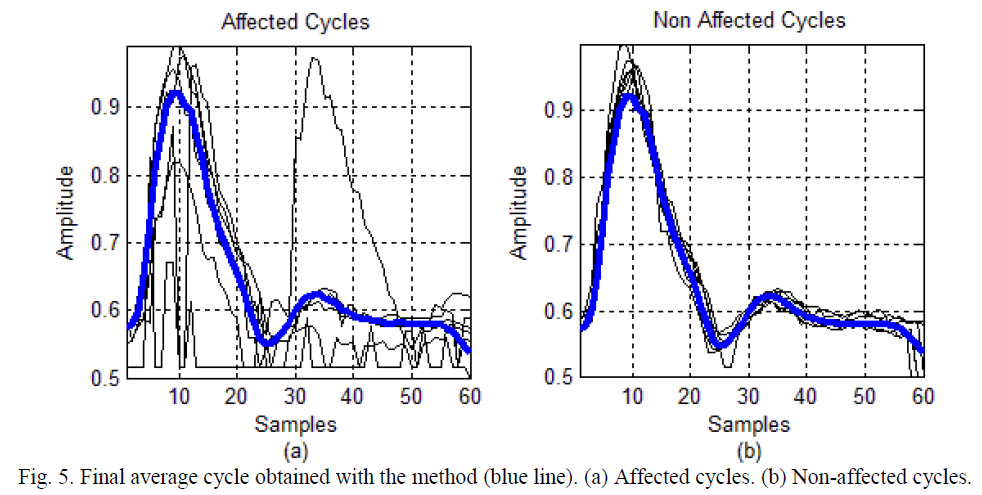 |
| As shown in Fig.5, there is a significant difference between the cycles detected as affected and the final average cycle (Fig. 5.a) and between cycles detected as non-affected and the final average cycle (Fig.5.b). Non-homogeneous cycles (Fig. 5.a) show amplitude saturation at the bottom, which distorts the signal information and difficult to extract parameters for the determination of clinical indexesneeded for a correct diagnosis.Depending on the real application, the non-homogeneous cycles (or affected cycles) may be excluded for the estimation of the parameters needed for the clinical indexes computation [3]. |
ECG signal |
| The Fig.6 shown the 2500 samples of adenoised ECG signal sampled at 250 Hz. In addition, blue vertical dashed lines are used to delimit eachcardiac signal cycle.For a correct delimitation of the cycles, the Gaussian noise elimination techniques was applied firstly. |
 |
| As it can be seen in Fig. 6, the cycles 2, 3 and 4 of the ECG signal exhibit a completely different morphology from the rest. The goal is to identify these cycles, which will reveal the source of noise that originated them. |
| As in the previous example, once the cyclesare delimited, the noise varianceis estimated, using wavelet decomposition. Then, a real value for the parameter ïÿýïÿýis proposed and the detectionthreshold is determined using (10). Then it is possible identify the no-homogeneous cycles of the ECG signal, estimating the mean square error for each cycle and comparing it with the detectionthreshold using (9). The result of all of these operations is shown in Fig. 7. |
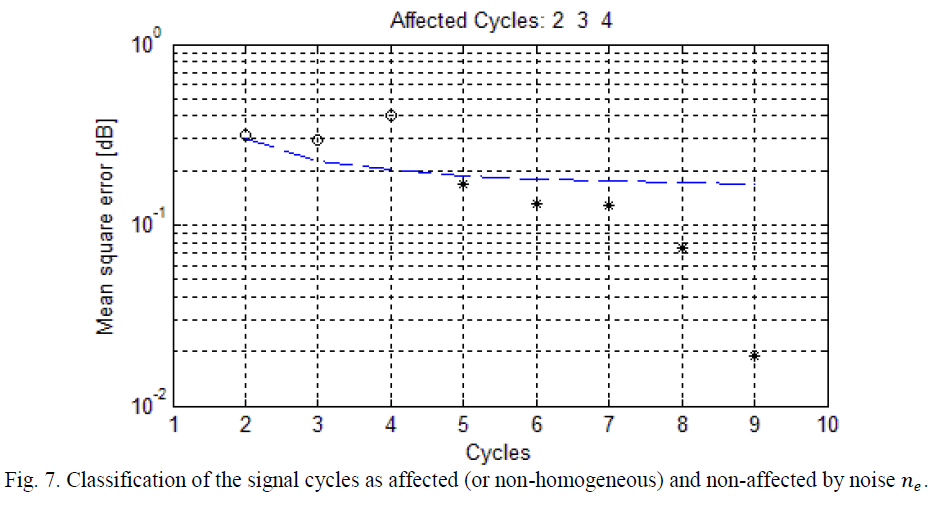 |
| In Fig.7, the cycles detected as affected by any noise source ïÿýïÿýïÿýïÿý are marked with circles, and cycles detected as unaffected are marked with asterisks. The blue dashed line represents the detectionthreshold. It should be noted that cycles detected as affected match the segment of the signal shown in Fig. 6, which exhibited a behavior different from the rest. |
| The identification of these non-homogeneous cycles, and its possible exclusion of the signal analysis, is useful for detection of important characteristics (complex QRS detection, arrhythmias, tachycardia, cardiac frequency, heart attack, etc.) for a correct diagnostic of the patient [3]. |
CONCLUSION |
| A method for detecting non-homogeneous cycles in quasi-periodic signals was proposed. Such detection is made based on comparisons with a threshold and the estimation of the variance of inherent noise affecting the signal under study. The method is independent of the signal carrying useful information and of the characteristics of distortions to be identified, which is an advantage over the most widely used methods such as those based on wavelets. |
| The application of the method on two real signals, one of blood flow and other of ECG, was shown. Satisfactory results were obtained and was possible to identify the cycles of these signals which were affected by any noise component ïÿýïÿýïÿýïÿýand do not constitute a source of reliable information for diagnosis. |
References |
|