Swarm Intelligence Paradigm For
Object Tracking In Video

Abhijit Kamune; Manjusha Dhabale

Swarm Intelligence Paradigm For Object Tracking In Video

Abhijit Kamune¹ , Manjusha Dhabale²

Assistant Professor, Department of Computer Science and Engineering, Ramdeobaba College of Engineering , Nagpur, India
Assistant Professor, Department of Computer Science and Engineering, Ramdeobaba College of Engineering , Nagpur, India

Related article at Pubmed, Scholar Google

Visit for more related articles at International Journal of Innovative Research in Computer and Communication Engineering

Abstract

Object tracking is an important task within the field of computer vision. The high-powered computers, the availability of high quality and inexpensive video cameras, and the increasing need for automated video analysis has generated a great deal of interest in object tracking algorithms. In this paper, we are proposing a new object tracking algorithm that employs a swarm-intelligence based method, particle swarm optimization (PSO).Firstly, all potential solutions are projected into a high-dimensional space where particles are initialized. Then, particles are driven by PSO rules to search for the solutions. The object is tracked when the particles reach convergence. In this paper, we are going to track the Table Tennis Ball, as Ball tracking is very challenging task because of the ball speed, illumination changes, and overlapping of the object. We are using color as feature to uniquely identify the ball and calculate the fitness function, which are used in PSO to drive the particles towards the ball.

Keywords

Object, Swarm, Particle, Fitness Function, gBest, pBest, PSO

INTRODUCTION

Object tracking is the problem of estimating the positions and other relevant information of moving objects in image sequences. The efficient tracking of visual features in complex environments is a challenging task for the vision community. Real-time computer vision applications such as surveillance and monitoring, robotics, authentication systems, perceptual user interfaces, all require the ability to track moving objects.

Numerous approaches for object tracking have been proposed [1, 2, 3, 4].Each having strengths and weaknesses. These algorithms are mainly classified based on which type of object representation and feature used to define the object.

Background subtraction is the most popular detection method used in object trackers [1], where color observations of individual pixels in a reference frame is statistically model. The problems with this method are sensitive to illumination changes, provides incomplete object regions and difficult to form background model. In [4] Transformation-Based Object Tracking non-rigid objects cannot be performed by using rigid-body motion models (like elliptical, rectangle etc.) In our present work, we are using Swarm Intelligence Paradigm for Object Tracking.

In [5] it describe Snake model for object tracking in which they used the energy function for tracking object characteristics. In [6] kernel based model are used where object track by using elliptical, rectangle and point as kernel shape are used to track the object. The shape is used according to application.

PROPOSED METHOD

As previous method required apriori knowledge of structure, boundary, skeletons, and other dynamics, where is in PSO (Particle Swarm Optimization) needs a set of distinct properties of an object in the video .i .e PSO will work without apriori knowledge of an object. Thus we need to develop adaptive tracking system with knowledge building process, hence the machine learning strategies and artificial intelligence paradigm need to employ when inadequate knowledge about an object which we are interested to track.

Particle swarm optimization algorithm [7] is a kind of evolutionary computation technique developed by Kennedy and Eberhart in 1995. It is similar to other population-based evolutionary algorithms in that the algorithm is initialized with a population of random solutions. Unlike most of the other population based evolutionary algorithms, however, each candidate solution (called particle) is associated with a velocity and position in search space. In [7, 8, 9] at each time step, the movement of particles is influenced by both its cognitive as well as its social components, as follows. Each particle has a velocity, which is modified according by the weighted influence of pbest and gbest. The larger is the difference between the current positions of the particle to pbest, the more it is influenced to go towards it. The same occurs for gbest (Eq 1) shows how the velocity of the ith particle is updated in the next time step (t + 1), according to its current position xi t at time t.

PROBLEM FORMULATION

Object tracking in given video is similar to identification of trajectory of an object. As video is collection of frame, the object tracking can be stated as sequence of locations. Hence tracking problem can be formulated as finding location frame by frame. The identification of location can be viewed as search problem, any optimal search strategy can employed to this problem, mathematically the Object Tracking problem stated as below. Find,

argmin d(w(x(t)),I(t)))

Where, d is distance between the element w(x(t)) and the frame of the video at

time t w.r.t object to be track

x(t) is location in the t th frame.

I(t) t’th frame in video.

w(x(t)) is picture element located at x(t) expected to represent tracking object.

x(t) should obey feasibility criteria like desired its continuity and physical constraints.

w(x(t)) should obey structural constraints ,geometric property of an element.

The last two constraints properties are essential for addressing realistic aspects which will take coupling factor frame to frame. To reduce the complexity of the problem one can ignore last two constraints initially.

A. Fitness Function

We are addressing a ball as object to be track, so we selected a RGB as object feature. The object feature are used to make fitness function which is minimization function. Here we are using following fitness function which is used to drive the particle towards the object.

OP : Object Characteristics i.e RGB value

PCP : Each individual particle characteristics

DT=OP-PCP;

Fitv = DT*DT';

In this fitness function we used Square of Euclidian distance between feature vector of object and particles.

B. Initial Particle Generation

Initial population generation has been addressed in this dissertation in three different ways. It is demonstrated to accommodate less complex method (decouple) to complex (accommodate coupling factors)

Particles can generate by following methods:

1. Non-Parametric Based

2. Parametric Based.

1. Non-Parametric Based Particle Generation

Each frame is treated as independently without considering any learning i.e known as Non-parametric particle generation. The particles are generated with standard uniform distribution, with open interval (0,1).Particles are generated in specified window, having their own characteristics.

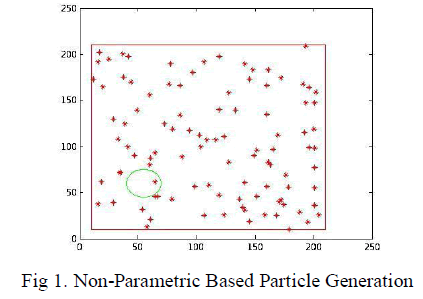NP: Number of Particles.

PC: (NP*2), particles (x,y) location

a,b are used for rectangle dimension.

PC=[rand(NP,1)*(b-a)+a rand(NP,1)*(b-a)+a];

rand() generate Uniformly distributed pseudo random numbers

2. Parametric Based Particle Generation

In this method also each frame treated as independently but previous frame recommended the location of the object in current frame. Thus non-uniform sampling method with (bi-varatre normal distribution.) is used to generate the particles. In this method we are using two statistical measures to add some knowledge for particle generation .Here we are generating a particle with help of some knowledge acquired from previous frame. The knowledge is in the form of weighted sum of the particles converges in last frame. The randn() function is using the Mean and Standard Deviation to generate the particle with Normally distributed Random number.

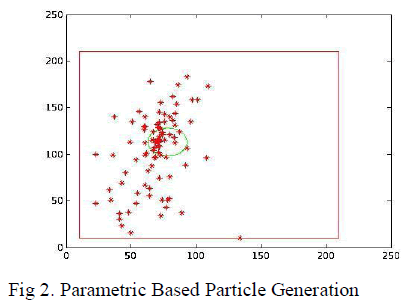NP: Number of Particles.

PC: (NP*2), particles (x,y) location

mu(2*1) : Mean location (x,y)

st(2*1): Standard Deviation

a,b are used for rectangle dimension.

1.96 is approx 97.5 percentile point of the normal distribution used in statistics.

st=min(abs(a-mu),abs(b-mu))/1.96;

PC=[ mu(1)+(1.96)*st(1).*randn(NP,1)

mu(2)+(1.96)*st(2).*randn(NP,1) ]

Here we are using randn() function which are using Normally distributed pseudo random numbers generation.

SIMULATION RESULTS

1. Particle converges in first frame

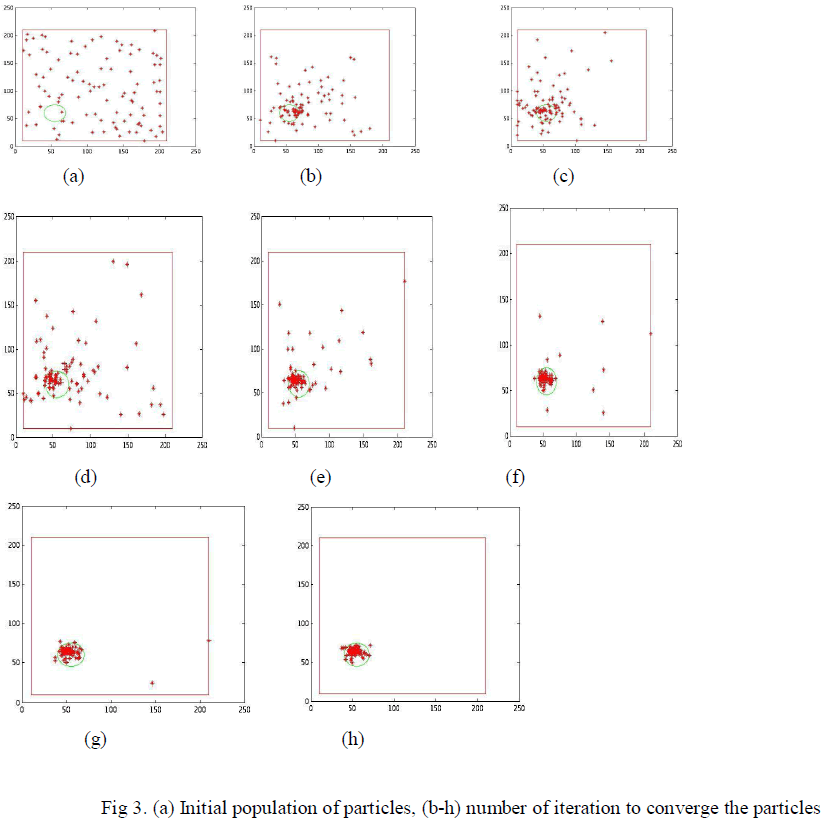In above figure it shows the tracking of object for first frame ,particles are generated randomly and it converge the object according to POS .

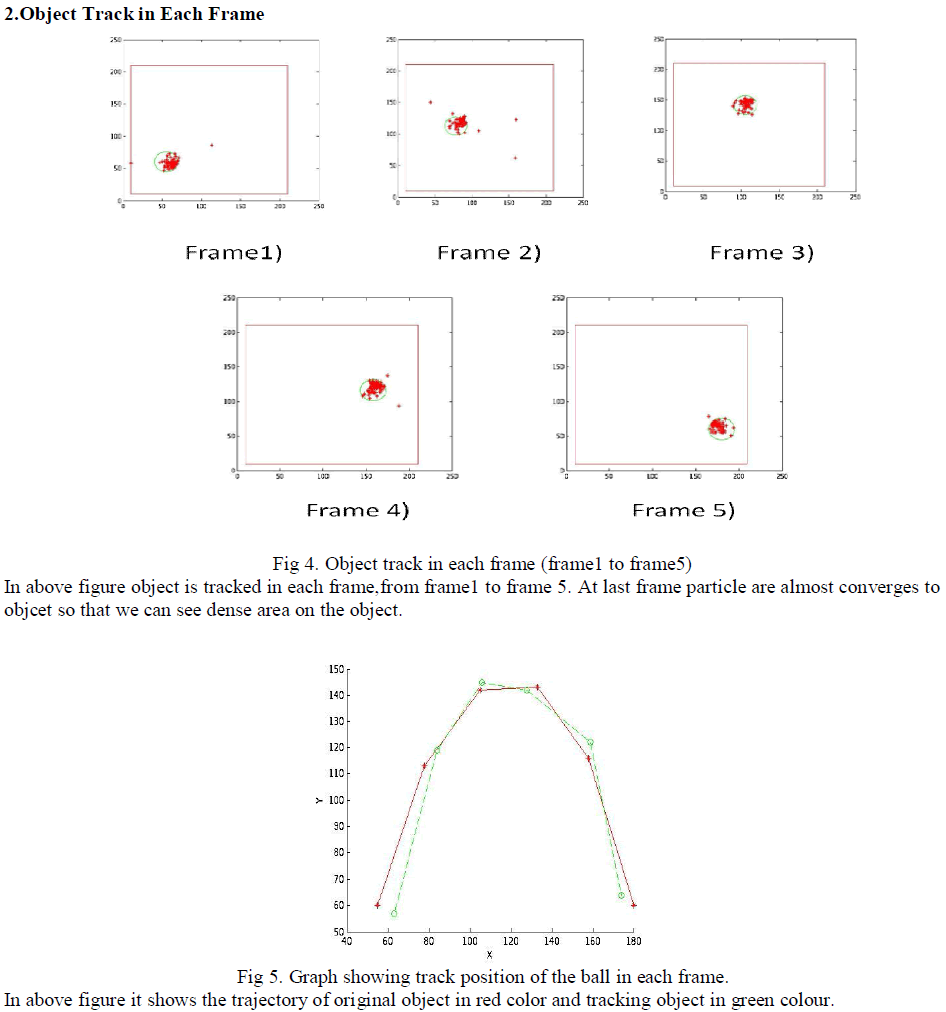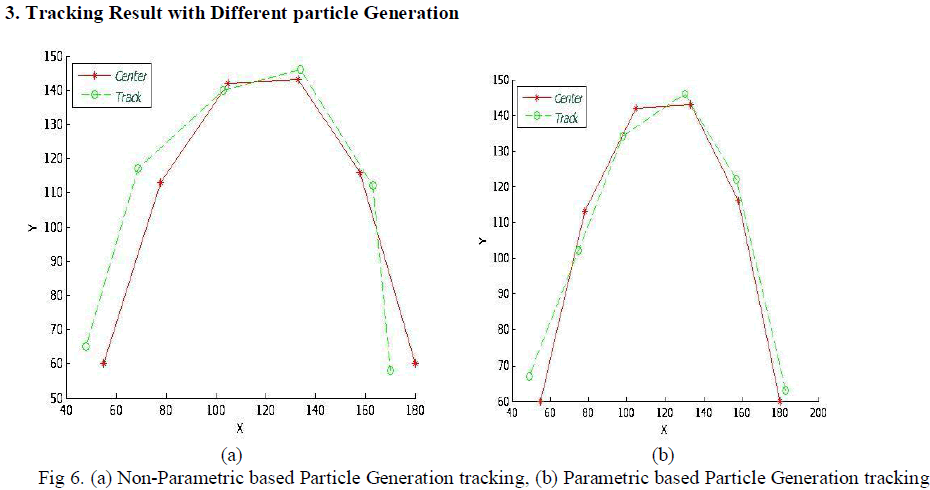The graph shows the actual position of the ball(object) centre in red color and track trajectory in green color.

Here in this diagram you can see the difference of tracking in parametric and non-parametric approach.

In parametric we have added some intelligence by using statistical measure.

4. Comparison of Non-Parametric and Parametric Methodsq

In these tables we are trying to compare the performance of the two methods based on different variations of PSO parameters .It is giving convergence time(sec) for each frame.

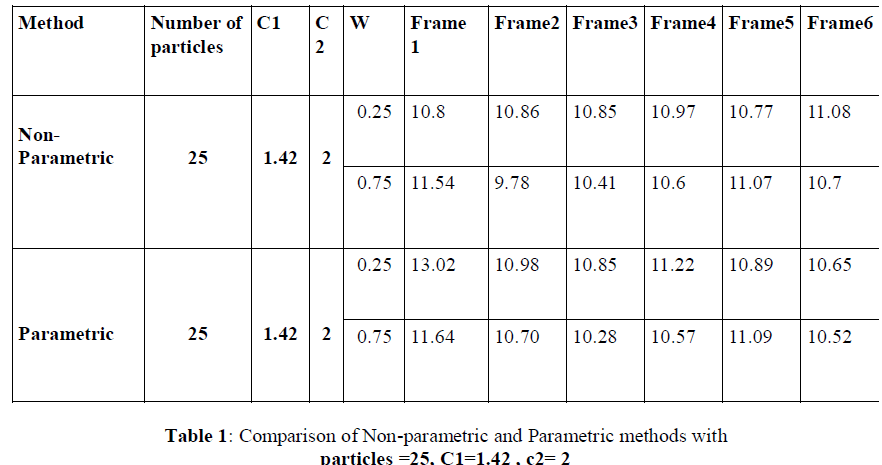In this table we are varying different PSO parameter and compare the result of parametric and non-parametric approach. Here particle size is only 25 ,with lowest pBest and gBest value .

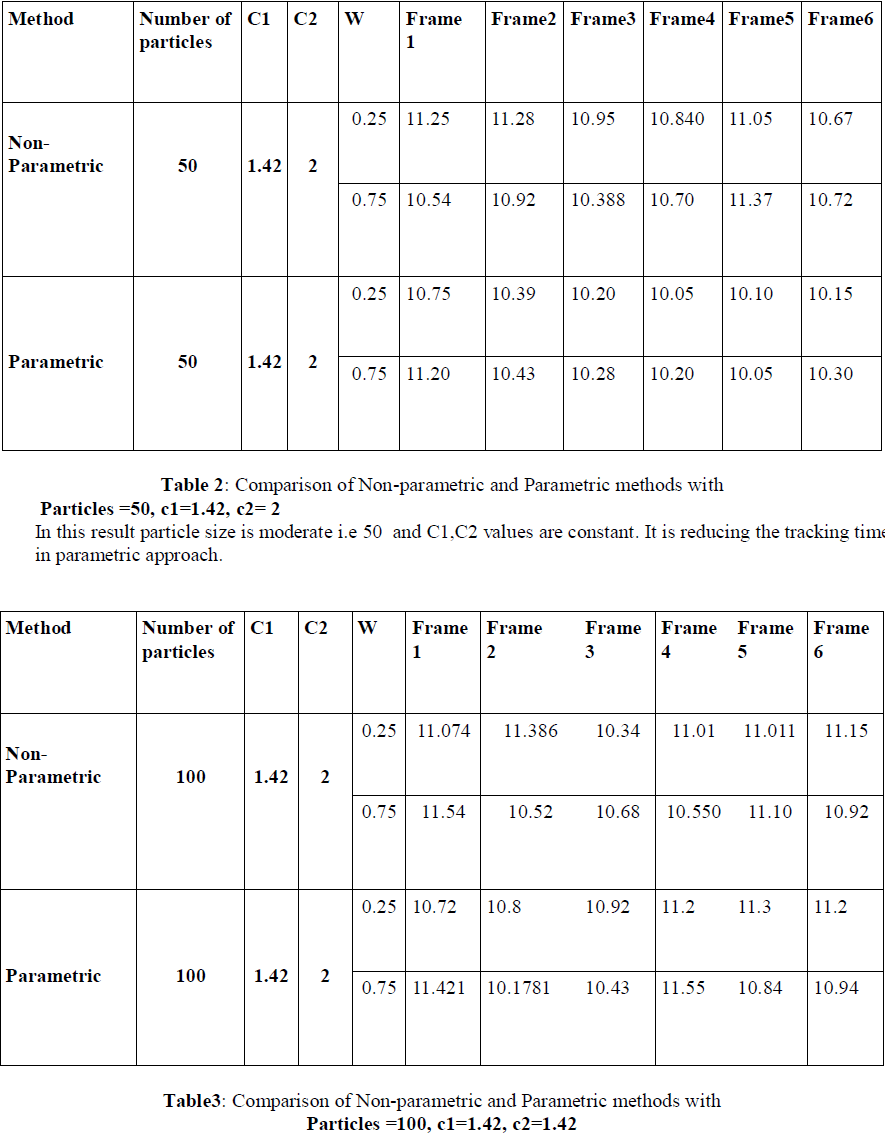In this result particle size is high i.e 100 and C1,C2 values are constant. It is reducing the tracking time in parametric approach.

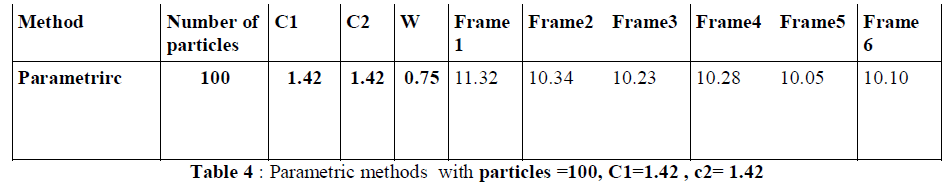In above table we have gone through different PSO parameter and their effect on tracking process. As we are increasing the number of particle and C1,C2 value we are getting good tracking result, we are getting close curve with respect to original object trajectory.

CONCLUSION AND FUTURE WORK

In this paper we have come up with new approach for object tracking using Swarm intelligence Paradigm. We have experimented different particle generation method like Non-Parametric and Parametric approach.

In parametric approach we have build the knowledge based by some statistical measure i.e mean and variance from previous frame history. It is giving good result compared to Non-parametric approach. The scope of the present work is limited to single object tracking.

References

Yilmaz, A., Javed, O., and Shah, M. 2006. Object tracking: A survey. ACM Comput. Surv.38, 4, Article 13 (Dec. 2006), 45 pages. DOI = 10.1145/1177352.1177355 http://doi.acm.org/10.1145/1177352.1177355
Maurin, B.; Masoud, O.; Papanikolopoulos, N.P.; , "Tracking all traffic: computer vision algorithms for monitoring vehicles, individuals, and crowds," Robotics & Automation Magazine, IEEE , vol.12, no.1, pp. 29- 36, March 2005 doi: 10.1109/MRA.2005.1411416
O. Javed and M. Shah, “Tracking and object classification for automated surveillance”, in ECCV, 2002, vol. 4, pp. 343-357.
JinchangRen; Vlachos, T.; Argyriou, V.; , "Immersive and perceptual human-computer interaction using computer vision techniques," Computer Vision and Pattern Recognition Workshops (CVPRW), 2010 IEEE Computer Society Conference on , vol., no., pp.66-72, 13-18 June 2010 doi: 10.1109/CVPRW.2010.5543161
M. Kass, A.Witkin, and D. Terzopoulos. “Snakes: active contour models”.Intl J. Comp. Vis., 1(4):321-331, 1987.
D. Comaniciu, V. Ramesh, and P. Meer, “Kernel-based object tracking”,IEEE Trans. Pattern Anal. Machine Intell,vol. 25, no. 5, pp.564- 577, May 2003.
Kennedy, J.; Eberhart, R. (1995). "Particle Swarm Optimization". Proceedings of IEEE International Conference on Neural Networks. IV. pp. 194-1948.doi:10.1109/ICNN.1995.488968.
YuhuaZheng and Yan Meng , A swarm-intelligence based algorithm for face trackingInt. J. Intelligent Systems Technologies and Applications, Vol. 7, No. 3, 2009
YuhuaZheng; Yan Meng; , "Swarm intelligence based dynamic object tracking," Evolutionary Computation, 2008. CEC 2008.(IEEE World Congress on Computational Intelligence). IEEE Congress on , vol., no., pp.405-412, 1-6 June 2008doi: 10.1109/CEC.2008.4630829
S. Besson, M. Barlaud, and G. Aubert, “Detection and tracking of moving objects using a new level set based method”, Proc. ICPR, vol. 3, pp. 1100-1105, Sept 2000.