Chris Mora*
Department of Mathematical Sciences, California State University, Bakersfield, United States
Received: 22-Mar-2021 Manuscript No. JSMS-23-94907; Editor assigned: 25-Mar-2021, Pre QC No. JSMS-23-94907 (PQ); Reviewed: 08- Apr-2021, QC No. JSMS-23-94907; Revised: 31-Mar-2023, Manuscript No. JSMS-23-94907 (R) Published: 28- Apr-2023,
DOI: 10.4172/J Stats Math Sci.9.1.001.
Citation: Mora C. The New Calculus. J Stats Math Sci. 2023;9:001.
Copyright: © 2023 Mora C. This is an openaccess article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Visit for more related articles at Research & Reviews: Journal of Statistics and Mathematical Sciences
Tangent lines; Derivatives; Asymptotic equations; Logical derivative
The basic problem of differential calculus is the problem of tangent lines and calculating the slope of the tangent line to the graph at a given point P and the less seemingly important problem of defining the vertical asymptote line and its derivative. L’hopitals indeterminate forms and extracting real value of asymptotic equations are easily solved by applying “the logical derivative”. These are new derivatives developed using a method of direct proportions. By reversing the decrement, all derivatives derived are of the same dimension as their functions.
Derivatives of increasing functions are similar in nature to increasing functions; and decreasing functions generate derivatives of decreasing nature-logical, but most of all sensible; It is now also possible to compute tangent line equations and also of those with vertical asymptotes [1].
Newton’s power rule based on lesser reasoning than required is now extended; summative expressed as a sum of linear terms; and the difference quotient is logically analyzed linear and directly proportional; flat tangent line equations of all functions are computed with the “logical derivative”.
Tangent lines for all points on a circle, ellipse, hyperbolas are derived viz. the method presented in my work. A proof for the interdependency between minimum and maximum points for all curves is employed and readily available should you ask for it and require publishing. Newton’s hypothesis of “instantaneous rate of change” remains the solid scaffold on which all calculus is based. The motivation and obsession for seeking further precision in Newton’s voluminous and monumental work [2-6].
Newton’s calculus revised
Logical derivatives

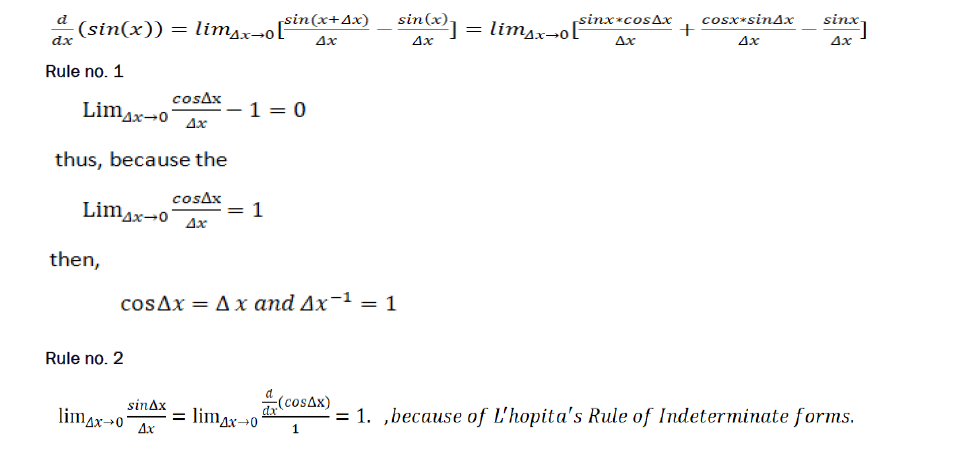


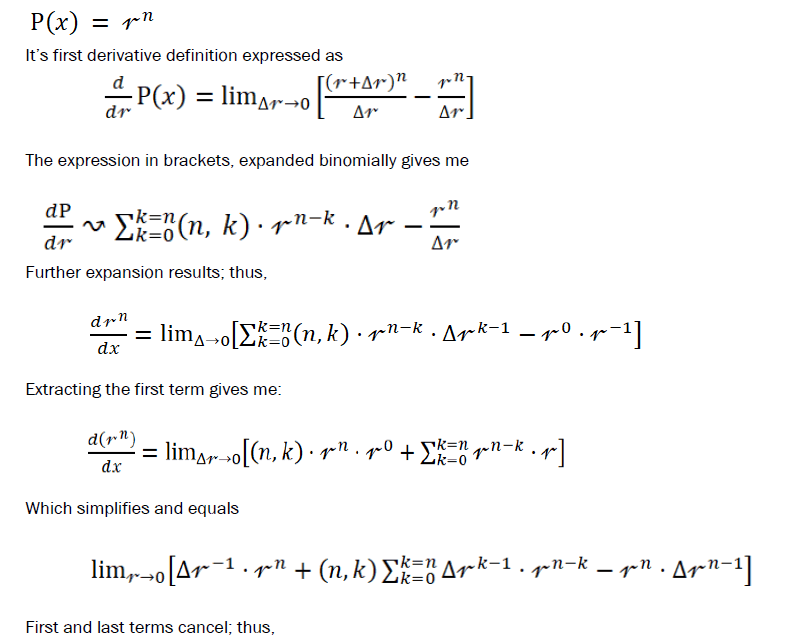

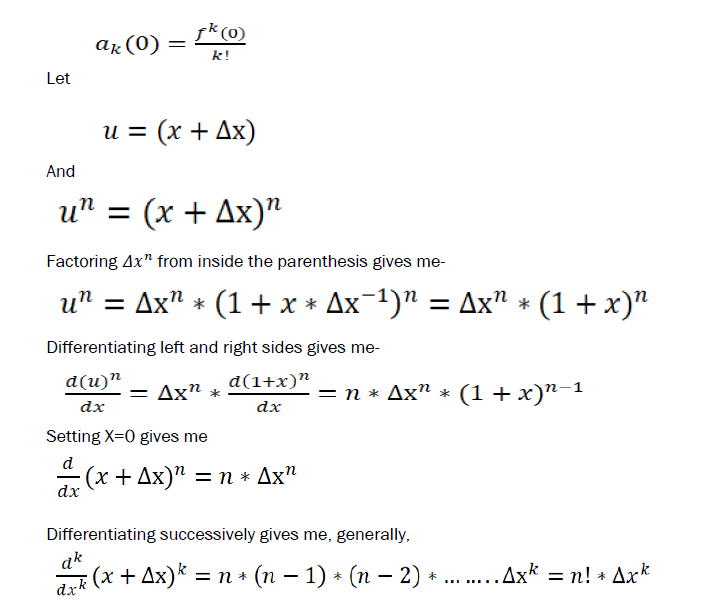


Example:
To find the tangent line at the origin of the graph I square both sides to get:
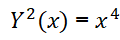
Differentiating both sides, implicitly for n=2; at the left side between 0 ≤ k ≤ 2
The derivative consists of 4 terms; thus,


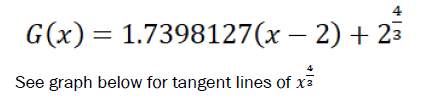



Method of solution of n-degree polynomial
Step 1. Square both sides.
Step 2. Implicitly differentiate the left and right side of the equation.
Step 3. Set the left side or the dependent side of the function equal to zero.
Step 4. Determine the solutions of the 2n-1 degree polynomial or the zeroes of the right side of the function of
-x.
Step 5. Step 4 determines the minimums and maximums of the n-degree polynomial.
Step 6. Determine the logical derivative of the n-degree function.
Step 7. Plot tangent lines of the minimums and maximums given I step 5.

[Crossref] [Google Scholar] [PubMed]