ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Soumyendu Bhattacharjee1, AishwaryaBanerjee1, SnehaDas1, Dr.Biswarup Neogi2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper presents the improvement of sensitivity of a system based on human heart, using PID tuning method. The Ziegler-Nichols method is used for PID tuning. For better result it is required to get desired performance specification in term of achieving maximum overshoot and specified settling time of the closed loop response .The proposed transfer function of heart and pacemaker is used in this paper with PID tuning to increase the sensitivity and Jury’s test which is a stability test used for Z domain stability has also been applied to analyse that this system is also stable in Z domain.
Keywords |
| PID Tuning, Sensitivity Analysis, Jury Stability Test. |
INTRODUCTION |
| Electronics pacemaker for human hearts regulates the speed of a heart pump. A proposed close loop system that includes a pacemaker and a measurement of the heart rate is shown in fig below [1]. The process of selecting the controller parameters to meet given performance specifications known as controller tuning [2]. In spite of all the advances in control over the past 50 years the PID controller is still the most common controller The PID tuning method is used to get the better simulation of the proposed control system [3].The most important reason behind this PID tuning approach is due to its simple control structure and satisfactory results. Ziegler-Nichols suggested rules for PID controllers. Here Ziegler-Nichols (Z-N) tuning rule is chosen as it is easy to implement during MATLAB simulation. In this tuning approach Z-N (PID Tunning) Method is used which is efficient and appropriate a system. |
II.SENSITIVITY ANALYSIS |
| The parameters of a control system have a tendency to vary due to change of environment conditions and this variation in parameters affects the desired performance of control system .The term sensitivity in relation to control system gives an idea of the system performance as affected due to parameter variations. Let the variable in a control system which changes its value be A such as output and this change is considered due to parameter variation of element K such as gain or feedback, then the control system sensitivity is expressed as- |
 |
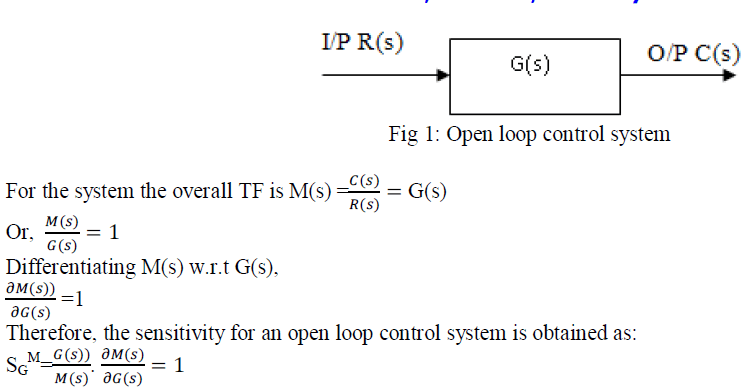 |
| (b)Sensitivity for Close loop control system: The basic block diagram of Close loop control system are given below in figure 2. |
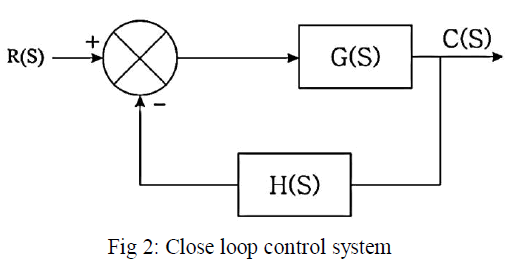 |
 |
| Comparing sensitivity functions, it is observed that the sensitivity of the overall TF with respect to forward path TF in the case of closed loop control system is reduced by a factor 1 + ïÿýïÿý(ïÿýïÿý)ïÿýïÿý(ïÿýïÿý) as compare to open loop system. [4] |
| (C) The sensitivity of overall TF M(s) with respect to feedback path TF: |
| The sensitivity of overall TF M(s) with respect to feedback path TF H(s) is written as: |
 |
| Comparing sensitivity functions, it is concluded that closed loop control system is more sensitive to variations in feedback path parameters than the variation in forward path parameters. |
III.SENSITIVITY ANALYSIS FOR THE GIVEN SYSTEM |
| (a) Sensitivity of overall transfer function with respect to forward path is given by: |
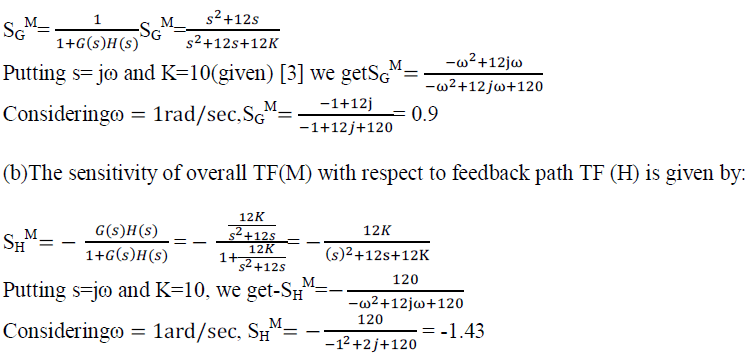 |
IV.FREQUENCY DOMAIN ANALYSIS OF GIVEN SYSTEM |
| (a) Routh’s stability criterion: |
| Routh’s-Hurwitz criterion is a mathematical test that is a necessary and sufficient condition for the stability for linear time invariant or LTI system. |
| In Routh-Hurwitz Criterion stability, the system is stable if and only if all the elements in the first column have the same algebraic sign. The importance of the criterion is that the roots P of the characteristic equation of linear LTI system with negative real parts represent solution eptof the system that are stable. Thus this criterion provides a way to test whether a system is stable or not. |
| The characteristic equation, a0sn+a1sn-1+................an-1s+an= 0 |
| Where, a0≠0 and an>0, and the co-efficient a0,a1,a2,.............are all of the same sign. |
 |
 |
V. STABILITY ANALYSIS OF A CLOSED LOOP SYSTEM IN Z DOMAIN |
| The stability is the most important parameter in control system.Thus stability of a closed loop system is given as |
| It can be determined from the location of closed loop poles in the Z plane which are the roots of the characteristic equation. |
| (a) Jury’s Test: |
| Jury’s test is used to analyse if any LTI(linear time invariant) system is stable in Z domain or not .To check whether a system is stable in Z domain first criterion is to check the characteristic equation against a number of specific rules and requirements.[5] |
| (b) Specific rules: |
| The characteristic equation D(Z)=a0+a1z+a2z2+…………………………...+aNzN |
| Being the highest degree of the polynomial .This test determines the pole outside of the unit circle. |
| 1: If Z=1 the system must be positive D(1)>0 |
| 2: If Z=-1 then (-1)ND(-1)>0 |
| 3: The value of constant term a0 must be less than the highest coefficient aN. |a 0|<|aN| |
| 4: Once Jury’s array has been constructed it automatically satisfies the following conditions |
| |b0|>|bN-1 |, |c0 |>|cN-2 |, |d0 |>|dN-3 | |
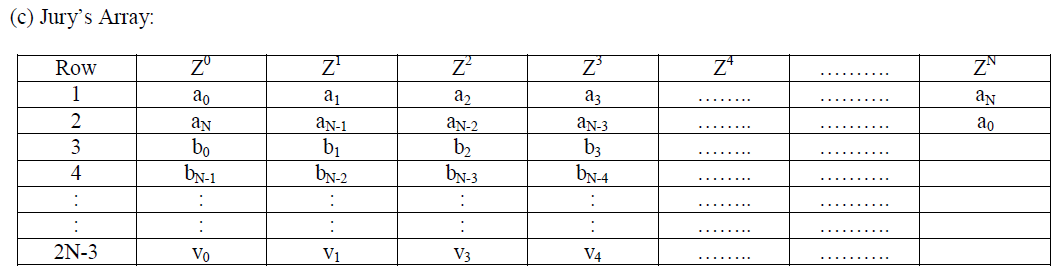 |
| (d) Stability analysis of given transfer function ̦́ in Z domain:Jury test is used to find out the stability in Z domain of the given system(Figure 3) |
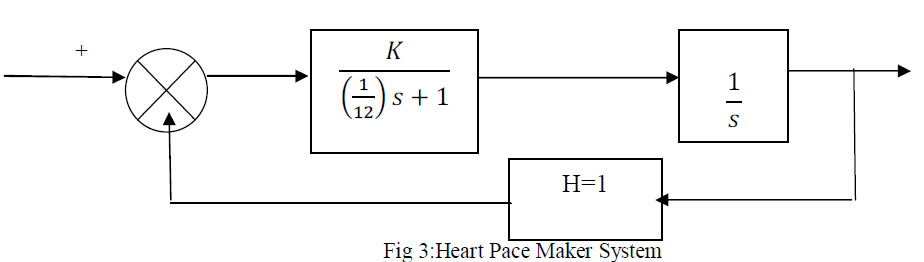 |
| In figure3 the heart-pacemaker system is given with a unity feedback, where the first block represents the transfer function of heart [6,7] and the second block connected in series represent the pacemaker system. |
 |
| Applying rule 2 in equation (iii) (-1)NF(-1)=(-1)2[37-58+25]=1×4 =4>0 |
| Applying rule 3 in equation (iii) a0=25 ,aN=37 ,so |a0|<|aN| |
| Construction of Jury’s array for equation (iii) |
 |
VI.APPROACH TO PID TUNNING |
| The proportional, integral, and derivative (PID) controller is widely used in the process industries due to its simplicity, robustness and wide ranges of applicability in the regulatory control layer. One survey of Desborough and Miller (2002) [8] indicates that more than 97% of regulatory controllers utilize the PID algorithm. Tuning a control loop is the adjustment of its control parameters (gain/proportional band, integral gain/reset, derivative gain/rate) to the optimum values for the desired control response. |
| (a) Manual Tuning: |
| If the system is online first all values are set to zero. Values are increased until the output of the loop oscillates and until the loop is acceptably quick to reach its reference after a load disturbance. However, too much will cause excessive response and overshoot. A fast PID loop tuning usually overshoots slightly to reach the set point more quickly. The main advantage of manual tuning is there is no requirement of math and online method. |
| (b) (Z-N) Ziegler- Nichols Method: |
| In 1942 Ziegler and Nichols described simple mathematical procedures for PID tuning [8]. Ziegler-Nichols tuning rule is a computational approach to search optimal sets of parameter values of PID controllers. Ziegler and Nichols proposed rules for determining values of parameters of PID controller - the proportional gain Kp, integral time Ti and derivative time Td. Table 1 shows the values of Kp, Ti and Td for PID Controller.[9] |
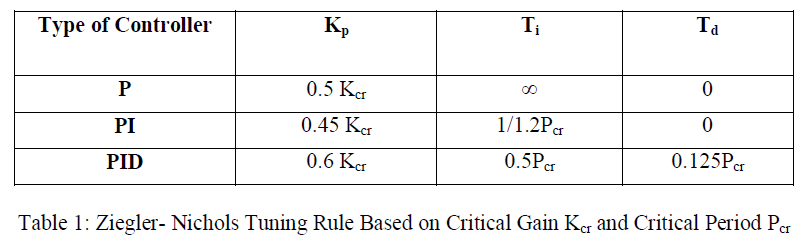 |
| So, PID controller tuned by the Ziegler – Nichols rule gives, |
| If the system has a known mathematical model (such as transfer function), then root locus method can be used to find out the critical gain Kcrand the frequency of sustained oscillations ωcr, where 2π/ωcr=Pcr |
VII.SIMULATION RESULT AND SENSITIVITY ANALYSIS WITH PID TUNING APPROACH |
| PID controller consists of Proportional Action, Integral Action and Derivative Action. PID controllers can then be designed by using Ziegler-Nichols method. Tuning method for the basic PID control is commonly known as Ziegler- Nichols tuning rule (Z-N). |
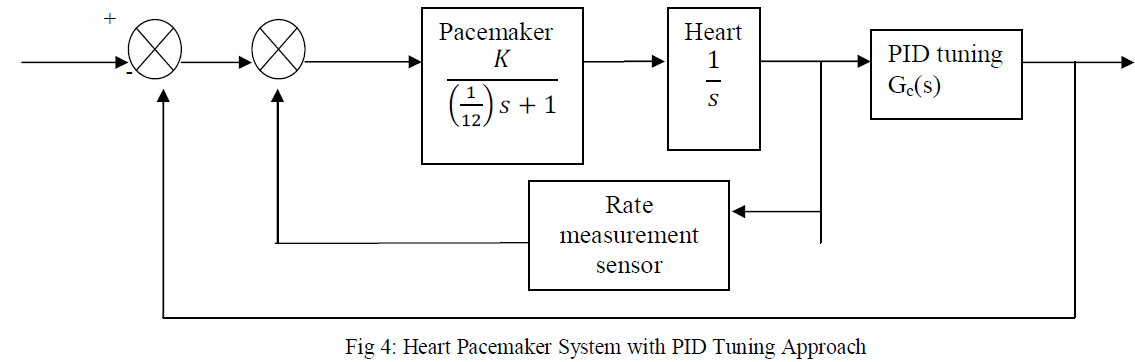 |
| Here the heart-pacemaker system is connected with a PID tuning shown in fig4 with a unity negative feedback. Now the PID [10] controller is to be designed to improve the sensitivity and settling time. |
 |
| The value of Kpthat makes the system marginally stable so that sustained oscillation occurs can be obtained by Routh’s stability criteria. Since the characteristic equation for the closed-loop system is |
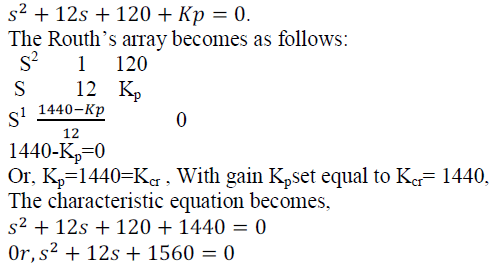 |
| To find the frequency of the sustained oscillation, s=jω is substituted into the characteristic equation. So it becomes, |
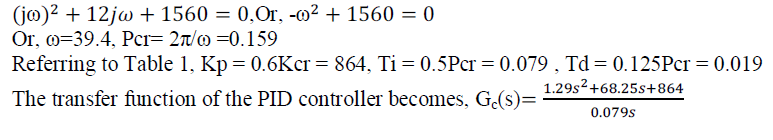 |
 |
| In the figure 5 the transfer function of heart-pacemaker system is connected with the PID controller with negative feedback to examine the time response. |
| So, the closed loop tuned transfer function to examine the unit-step response of the system is |
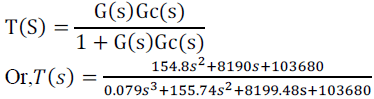 |
| (b) MATLAB code and Simulation result: The MATLAB code and step response(taking different value of damping factor) for Heart Pacemaker system without PID tuning and with PID tuning are given below. |
 |
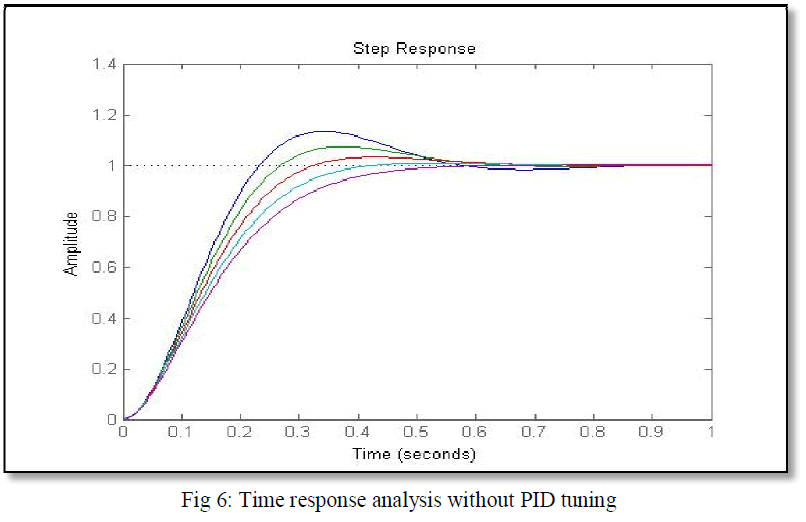 |
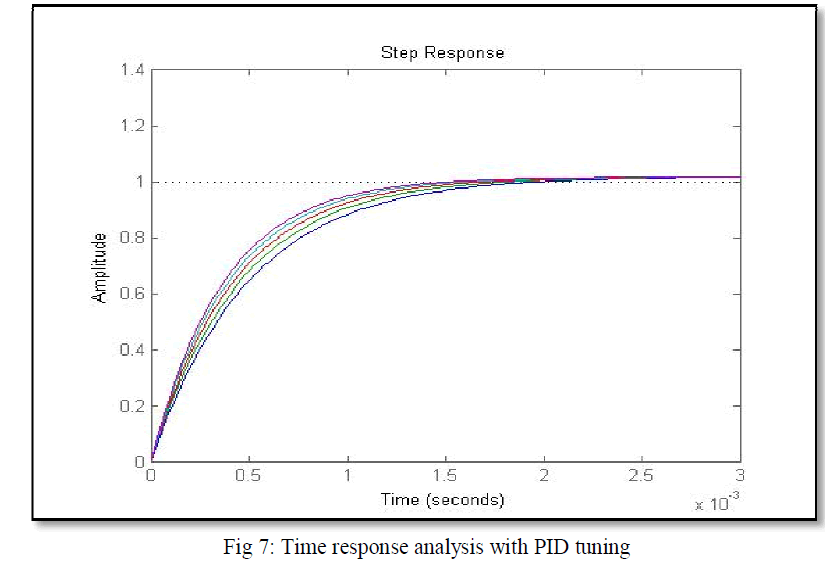
| Figure 6 and Figure 7 shows the simulation result of Time response analysis without PID tuning and Time response analysis with PID tuning for different values of damping factor. |
| (c)Sensitivity Analysis with PID Tunning: |
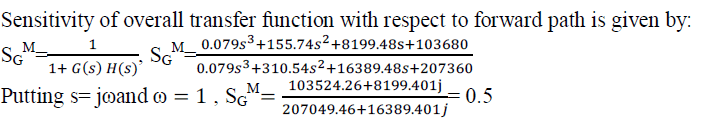 |
 |
VIII.COMPARATIVE STUDY OF THE SYSTEM |
| (a) Simulation Results Analysis: |
| By studying response and stability criterion of the system, it is seen that after PID tuning i.e., the close loop configuration of Heart Pacemaker system has been improved a lot. The transfer function with PID tuning response shows least settling time with optimal overshoot. |
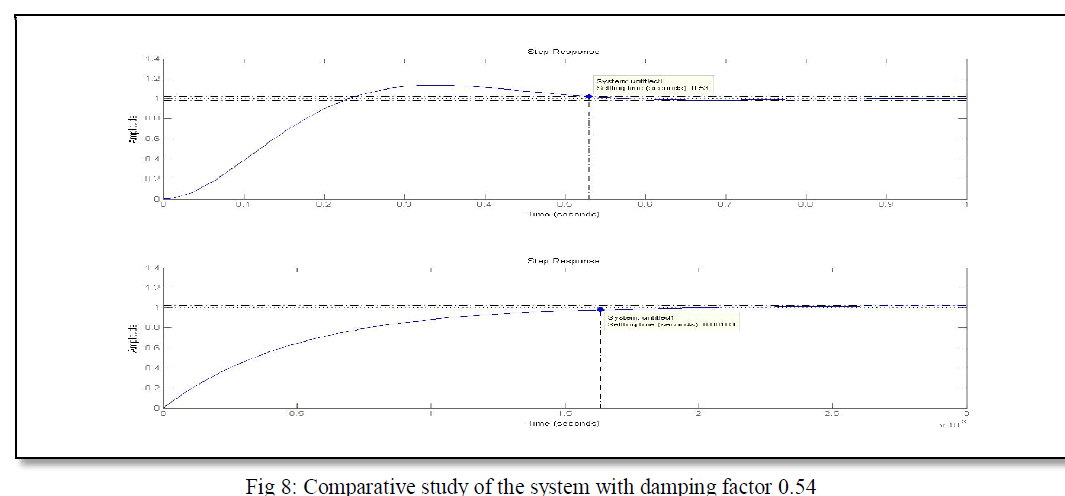 |
| From figure 8, given below it is observed that, considering damping factor .54, the settling time without PID tuning is .53 second, where as the settling time with PID tuning is .0016 second. From figure 6 and figure 7 it is also observed that, for different values of damping factor the settling time and overshoot with PID tuning will be died down. |
(b) Sensitivity Improvement: |
| From the above two figures that is fig 3 and fig 4 the calculated sensitivity of overall transfer function with respect to forward path is 0.9 and 0.5 respectively. As the definition says due to change of environment conditions the parameters of a control system may vary. This variation affects the desired performance of a control system. So, much the affect or sensitivity reduces the desired performance of the control system increases. Here the result is very much convenient for the heart pacemaker system. |
IX.CONCLUSION |
| The Z-N tuning would serve as the basis for the upcoming new generation of PID technology as it provides improved performance, low cost, and training compared to other tuning methods like Cohen coon, trial and error method etc. It can be embedded into established, convenient generalized controller products. So from all the analysis done above in all calculation a conclusion can be made that the sensitivity and settling time of the proposed system increases as well as that system will be able working in both the S and Z domain. The MATLAB code is built considering its importance in analysing the behaviour of any system of the model type as described above and its tuned output response based on its input. |
References |
|