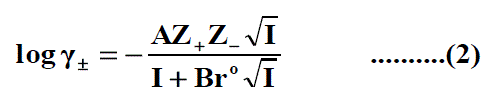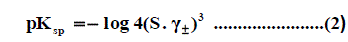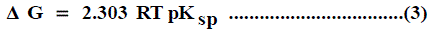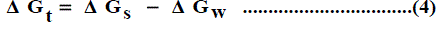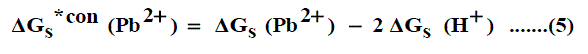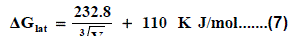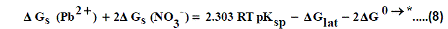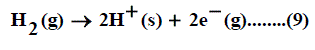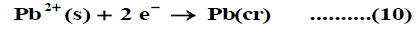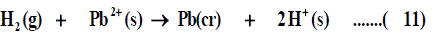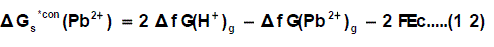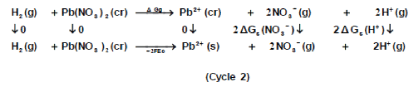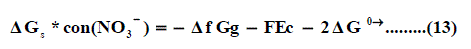Thermodynamics of the Solvation of Lead Nitrate in Mixed Propanol-H2O Solvents at Different Temperature
Esam A Gomaa1* and Elsayed M Abou Elleef2, Ahmed Fekri1, Mohamed Khairy3 and Reham M Abou Karn1
1Chemistry Department, Faculty of Science, Mansoura University, 35516-Mansoura, Egypt.
2Basic Science Departments, Delta Higher Institute for Engineering & Technology, 35681- Dakhlia, Mansoura, Egypt
3Chemistry Department,Faculty of Science,Benha University,Beha,Egypt.
- *Corresponding Author:
- Esam A Gomaa
Chemistry Department
Faculty of Science
Mansoura University
35516 - Mansoura, Egypt.
Received: 18/05/2014 Accepted:19/06/2014 Revised: 13/06/2014
Visit for more related articles at Research & Reviews in Pharmacy and Pharmaceutical Sciences
Abstract
The aim of this study was to determine the thermodynamics of the solvation of Pb(NO3)2in mixed propanol-H2O solvents , which is very toxic heavy metal salt at different temperatures. The Gibbs free energies as very important thermodynamic property were evaluated for Pb(NO3)2 in mixed propanol-H2O solvents at different temperature from the experimental solubility measurements. The ratio of the ionic radii between lead and nitrate ions was used to divide the total Gibbs free energy of the salt into its individual contribution in the mixtures used. Libration Gibbs free energy associated with the moving Pb(NO3)2 in standard gas state to standard state in solution was evaluated according to specific cycle for the solvation process using the solubility product. Also the lattice energy for Pb(NO3)2(cr) was also calculated and used for further evaluation (the symbol (cr) denotes the crystalline phase). The conventional Gibbs free energies for the cation (Pb2+) and anion (NO3-) were estimated theoretically and also the Gibbs free energy of NO3- gas was evaluated and all values were discussed.
Keywords
Thermodynamic, Pb(NO3)2, Gibbs free energy of solvation, lead nitrate, aqueous- propanol mixtures, conventional free energies.
Introduction
For neutral species experimental solvation Gibbs free energies have been tabulated large number of solutes in both aqueous [1-7] and non-aqueous [7,8] solvents. Typically, these solvation free energies are determined experimentally [8] and their uncertainty is relatively low (~ 0.8 KJ/mol) [9].Determining accurate values for the Gibbs free energies of ionic solutes like Pb(NO3)2 is important than that of neutral solutes. Single-ion solvation free energies are well defined in statistical mechanics, and determining their values is an important step in understanding the structure of solutions. Understanding the partitioning of single ions between different liquid phases is important in many areas of biology. For example, the electrical signals sent by nerve cells are activated by changes in cell potential that are caused by the movement of various ions (sodium and potassium) across the neuronal membrane [10]. The division of thermodynamic Gibbs free energies of solvation of electrolytes into ionic constituents is conventionally accomplished by using the single ion solvation Gibbs free energy of one reference ion, conventionally, the proton, to set the single ion scales [11,12].Sums of solvation free energies of cations and anions are well defined through the use of thermochemical cycles involving calorimetric or electrochemical measurements [13-17]. A number of different extra thermodynamic approximations have been used [18-22] for partition the salt Gibbs free energies into single ion contribution. The aim of this work is to estimate the single ion Gibbs free energies for Pb2+& NO3- ions in mixed propanol-H2O solvents at different temperature.
Relative and Conventional Solvation Free Energies of Ions
The Gibbs solvation free energies of ions are often tabulated as relative free energies by setting the free energy of solvation of some reference ion equal zero [23]. Proton was chosen as reference ion. For ions, this result in a set of conventional free energies of solvation that the cations are shifted from their absolute values by the value for the absolute Gibbs solvation free energy of the proton. The conventional Gibbs free energies of solvation for anions are shifted by an equal amount in the opposite direction.
Conventional Gibbs free Energies from Reduction Potentials
When the convention for the absolute Gibbs free energy of the proton is followed, the solutionphase free energy change associated with the half cell for reaction of hydrogen gas is equal to zero. Reduction potentials following this convention for hydrogen electrode are referred as standard reduction potentials. From the half cell reaction for the reduction of metal cation to crystalline phase and the half reduction reaction of hydrogen gas, the redox reaction can be illustrated through the use of thermochemical cycle [12]. This last procedure can be used to estimate the gas free energy of formation of NO3- ion, to explain the ionic behavior.
Materials and Methods
Lead nitrate Pb(NO3)2 GCC-laboratory reagent and propanol (Pr-OH) from Merck Co. were used. Saturated solutions of Pb(NO3)2 were prepared by dissolving different amounts in closed test tubes containing different Propanol-H2O mixtures. These mixtures were then saturated with nitrogen gas an inert atmosphere. The tubes were placed in a shaking thermostat (ModelDW101S) for a period of four days till equilibrium reached. The solubility of Pb(NO3)2 in each mixture was measured gravimetrically by evaporating 1 ml of the saturated solution in small beaker using I. R. lamp. The measurements were done by three readings for each solution at 293.15K, 303.15K and 315.15K.
Results and Discussion
The molar solubility (S) for Pb(NO3)2 at 293.15K, 303.15K and 315.15K were measured gravimetrically with average of the second number after comma in water, propanol and their mixtures. The solubility values for Pb(NO3)2 are cited in Table 1, Table 2 and Table 3 . The mean activity coefficient (log γ±) of ions which can be estimated from the Debye-Hückel limiting law, as modified by Robinson and Stokes [24-80].
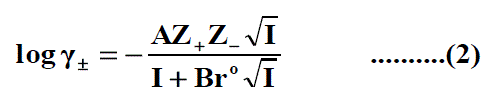
Table 1: Solubility, activity coefficient, solubility product, Gibbs free energies change and transfer Gibbs
free energies change for Pb(NO3)2 in mixed propanol-H2O solvents at 293.15 K.
Table 2: Solubility, activity coefficient, solubility product, Gibbs free energies change and transfer Gibbs
free energies change for Pb(NO3)2 in mixed propanol-H2O solvents at 303.15 K.
Table 3: Solubility, activity coefficient, solubility product, Gibbs free energies change and transfer Gibbs
free energies change for Pb(NO3)2 in mixed propanol-H2O solvents at 313.15 K.
Where Z + and Z - are the charges of ions in solutions, A= 1.823 ×106(ε.T) 3/2 , B = 50.29 (ε.T)-½, r° is the solvated radius, εis the dielectric constant of the solvents and S is the molar solubility. The values of ε for propanol-water mixtures were taken from previous publication [26]. These data ( log γ± ) were tabulated also in Table 1, Table 2 and Table 3. The solubility product was calculated by the use of equation (2) [27-90].
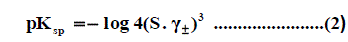
The solubility product (pKsp) data are given in Table 1, Table 2 and Table 3 from these solubility products, the Gibbs free energies of solvation and the transfer Gibbs free energies from water to organic solvent and mixed solvents were calculated by using equations (3) and (4) [29-96]. Their values are tabulated also in Table 1, Table 2 and Table 3.
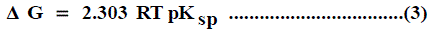
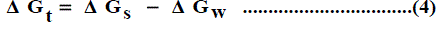
Where (s), (w) denote solvent and water, respectively.
It was concluded that the Gibbs free energies of transfer ( Δ Gt ) increase in negativity by increasing the mole fraction of propanol in the mixed Propanol-H2O solvents indicating the spontaneous nature of Pb(NO3)2 solubilization. This is due to more solvation behaviour in the mixed solvents than that of water where the Gibbs free energy values provide information on whether the process conditions favor or disfavor Pb(NO3)2 solubilization in the aqueous carrier solution. Positive Gibbs free energy values indicate disfavorable conditions. (Figs. 1-3).
Figure 1: Transfer Gibbs free energies changes of (ΔGt) for Pb(NO3)2 versus the mole fraction (Xs) of
propanol at 293.15K.
Figure 2: Transfer Gibbs free energies changes of (ΔGt) for Pb(NO3)2 versus the mole fraction (Xs) of
propanol at 303.15K.
Figure 3: Transfer Gibbs free energies changes of (ΔGt) for Pb(NO3)2 versus the mole fraction (Xs) of
propanol at 313.15K.
Single Ion Gibbs Free Energies and Convention Gibbs Free Energies for Pb2+ and NO3- Ions
It was well known that the preferential single ion thermodynamic parameters depend on the-ionic radii of two ions (cation and anion). Therefore the ionic radii ratio between Pb2+and NO3-was evaluated from exact radii values given in literature [30-32] and found to be (132 nm/179 nm= 0.737). Multiplying this ratio by the Gibbs free energies of Pb(NO3)2 we get the ionic Gibbs free energies of Pb2+ion. This last value was subtracted from the Pb(NO3)2 Gibbs free energy and we obtain the Gibbs free energy for NO3- anion. The obtained values for single ions are presented in Table 4. The conventional Gibbs free energies (Δ Gs )*con(Pb2+) for Pb2+ ion in solvents are shifted from their absolute values by the absolute free energy of the proton [45-47] according to equation (5)
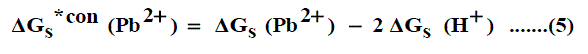
and for NO3- anion is shifted by an equal amount in the opposite direction (equation 6).

Where Δ Gs (Pb2+ ), Δ Gs (NO3- ) and Δ Gs (H+) are the Gibbs free energies of solvation for lead, nitrate and proton in solvents. From the mean values of proton solvation free energies in water and other solvents in literature [12,35,36] relation between these values and the diameter for each solvent taken from literature [37-40], a straight line was obtained. From this line the proton solvation free energies in pure water and propanol were obtained. Multiplying each value by its mole fraction in the mixture and then summing the results. The mixed solvent proton free energies were obtained and their values are given in Table 4. With equations (5) and (6) we get the conventional Gibbs free energies for the cation and anion and their values are given also in Table 4. Cation conventional free energy values are negative indicating exothermic character and anion values are positive indicating endothermic character. Both values increase with increase in the mole fraction of propanol due to more solvation and the sum of them gives the values for the neutral salt.
Table 4: Single ion Gibbs free energies for Pb2+ and NO3-1 and their half conventional free energies at
293.15K in mixed propanol-H2O solvents (kJmol-1).
Libration Gibbs Free Energies for Pb(NO3)2 in Mixed Propanol-H2O Solvents
The libration Gibbs free energies for Pb(NO3)2 in mixed propanol-H2O solvents at 293.15K, 303.15K and 313.15K were calculated following cycle 1 (thermochemical cycle 1) as done before [12] for silver salts following solubility product concept.
Where lat ΔG is the lattice free energy, (g) and (s) denote the gas and solution cases. The lattice energy was calculated following Bartlett’s relationship following equation (7) [30-50].
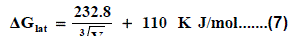
The volume of Pb(NO3)2 was calculated by dividing its molecular weight by the density of solid given in literature [40-96] and apply it in equation (7) to obtain 165.675 kJ mol-1 as ΔGlat for Pb(NO3)2. On the use of equation (8) after cycle (1), the libration free energies for Pb(NO3)2 was obtained (82.837 kJmol-1).
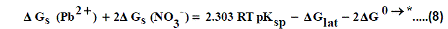
The 2ΔG0→*, the free energy change associated with moving Pb(NO3)2 from standard gas phase of one atmosphere to solution phase. This free energy change has been referred as” compression” work of the gas or libration free energy.
Conventional Free Energies from Reduction Potentials
The absolute Gibbs free energy of the proton is followed solution phase free energy change associated with the following half cell.
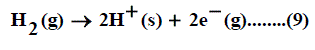
The half-cell reaction for the reduction of cation is:
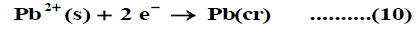
The symbol (cr) denotes the crystalline phase the sum of the two half cells are:
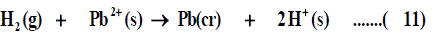
Through the use of thermochemical cycle 2, the conventional free energy for Pb2+ can be written as:
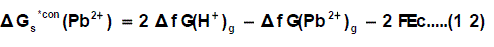
Where ΔfG(H+)g and ΔfG(Pb2+ )g are the gas free energy of formation for H+ and Pb2+ ions, F (faraday constant) = 96.485 kJ per volt gram equivalent and Ec is the standard reduction potential of Pb2+, Δ f G(Pb2+)g is difficult to evaluate because of the lack of exact ΔfG(H+)g value.
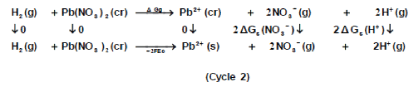
Also the conventional free energy of the nitrate anion NO3- can be written following Truhlar [41] explanation as:
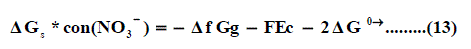
Applying equation (13) the ΔfGg , the gas free energies of formation for the anion NO3- was estimated in the mixed propanol-H2O solvents and their values are given in Table 4, 5 and Fig. 4. the ΔfGg ,value increase by increasing the mole fraction of propanol that favouring less solvation.
Table 5: Gas formation free for NO3-anion in mixed Propanol-H2O solvents at 293.15 K
Conclusion
Using a combination of experimental gas-phase free energies of formation and solution phase reduction potentials, we determined conventional solvation free energies of Pb(NO3)2 in mixed propanol- H2O solvents at 293.15K, 303.15K and 313.15K from the experimental solubility. Libration Gibbs free energy associated with moving Pb(NO3)2in standard gas state to standard stat in solution was evaluated according to thermochemical cycle for the solvation process using the solubility product. Also the lattice energy for Pb(NO3)2was also calculated and used for further evaluation. These conventional solvation free energies were then combined with experimental and calculated gas-phase free energies to determine conventional solvation free energies of ion-solvent clusters containing up to solvent molecules. The values for the absolute solvation free energy of the proton obtained in this work should be useful as standard against which the absolute solvation free energies of other single ions can be derived. For example, Table 4 shows the absolute single-ion solvation free energies of the ions considered in this work.
References
- Gabani S, Gianni P, Mollica V, Lepori L., Group contributions to the thermodynamic properties of non-ionic organic solutes in dilute aqueous solution. J Solution Chem. 1981;10: 563-595.
- Abraham MH, Whiting GS, Fuchs R, Chambers EJ., Thermodynamics of solute transfer from water to hexadecane. J ChemSoc Perkin Trans. 1990;2: 291-300.
- Leo AJ. Masterfile from Med ChemSofware; Biobytc.: Claremont, C.A.; 1994.
- Syracuse Research Corporation. Physical/Chemical Property Database (PHYSPROP); SRC Environmental Science Center: Syracuse NY. 1994.
- Yaffe D, Cohen Y, Espinosa G, Arenas AA. Giralt F. Fuzzy ARTMAP and back-propagation neural networks based quantitative structure-property relationships (QSPRs) for octanol-water partition coefficient of organic compounds. J ChemInfComput Sci. 2002; 42(2):162-83.
- Kelly CP, Cramer CJ, Truhlar DG. A Density Functional Theory Continuum Solvation Model for Calculating Aqueous Solvation Free Energies of Neutrals, Ions, and Solute Water Clusters. J Chem Theory Comput. 2005; 1: 1133-1152.
- Rizzo RC, Aynechi T, Case DA, Kuntz ID. Estimation of Absolute Free Energies of Hydration Using Continuum Methods: Accuracy of Partial Charge Models and Optimization of Nonpolar Contributions. J Chem Theory Comput. 2006; 2: 128-139.
- Cramer CJ, Truhlar DG. In Free Energy Calculation in Rational Drug Design, Reddy MR. Eds. Kluwer/Plenum: New York; 2001:63–95.
- Thompson JD, Cranier CJ, Truhlar DG. New Universal Solvation Model and Comparison of the Accuracy of Three Continuum Solvation Models, SM5.42R, SM5.43R, and C-PCM, in Aqueous Solution and Organic Solvents and for Vapor Pressures. J PhysChem A. 2004; 108: 6532-6542.
- Hodgkin AL. Ionic movements and electrical activity in giant nerve fibres. Biol Rev. 1951; 26: 339.
- Kelly CP, Cramer CJ, and Truhlar DG. “Single ion solvation free energies and the normal hydrogen electrode potential in methanol, acetonitrile and dimethylsulphoxide, J PhysChem B. 2007; 111(1): 408-422.
- Klotz IM, Rosenbery RM. Chemical Thermodynamics. 5th ed. Wiley: New York; 1994; P459.
- Tissandier MD, Cowen KA, Feng WY, Gundlach E, Cohen MH, Earhart AD, Coe JV, Tuttle TR. Jr. The Proton's Absolute Aqueous Enthalpy and Gibbs Free Energy of Solvation from Cluster Ion Solvation Data. J PhysChem A. 1998; 102: 7787-7794.
- Pliego Jr, Riveros JM. New Values for the Absolute Solvation Free Energy of Univalent Ions in Aqueous Solution. ChemPhysLett. 2000; 332: 597 -602.
- Llano J, Eriksson LE. First principles electrochemistry: electrons and protons reacting as independent ions. J Chem Phys. 2002; 117: 10193.
- Doménech A, Montoya N, Scholz F. Estimation of individual Gibbs energies of cation transfer employing the insertion electrochemistry of solid Prussian blue. J Electroanal Chem. 2011; 657:117–122.
- Krestov GA. Thermodynamics of Solvation: Solution and Dissolution, Ions and Solvents, Structure and Energetics. Ellis Horwood Ltd.: New York, 1991.
- Conway BE. Electrolyte solutions: Solvation and structural aspects. Ann Rev Phys Chem. 1966; 17: 481-528.
- Parker A. J. The effects of solvation on the properties of anions in dipolar aprotic solvents. Quart. Rev. Chem. Soc. 1962;16:163-87.
- Friedman HL, Krishnan CV. Thermodynamics of Ion Hydration in Water: a Comprehensive Treatise; Franks F. Ed.; Plenum Press: New York, 1973.
- Lewis GN, Randall M, PItzer KS, Brewer L. Thermodynamics, 2nd ed.; McGraw-Hill: New York; 1961; R: 399.
- Pradyot P. Handbook of Inorganic Chemicals. McGraw-Hill; 2002, ISBN 049439-8.
- Gomaa EA. Single ion free energies of some ion and the hydrophobic interactions of Ph4AsBPh4 and Ph4SbBPh4 in mixed ethanol-water solvents. ThermochimicaActa. 1989;156:91-99.
- El-Khouly AA, Gomaa EA, Abou El-leef S. Conductometry and solubility study of Cd2+-Kryptofix-22 complexes in various hydroorganic solvents. Bull Electrochem. 2003; 19(4):153-164.
- El-Khouly AA, Gomaa EA, Abou El-leef S. Apparent association constants of HgCl2 in presence of kryptofix –22 in mixed aqueous-organic solvents. Bull Electrochem. 2003; 19(5):193-202.
- Gomaa EA. AbouElleef EM, Mahmoud EH. Gibbs free energies for the solvation of KClO3 in DMF-H2O at 301.15 K. EurChem Bull. 2013; 2(10): 732-735.
- Gomaa EA. Solubility and solvation parameters of barium sulphate in mixed ethanol-water mixtures at 301.15 K. Int J Mater Chem. 2012; 2(1): 16-18.
- Gomaa EA, Al-Jahdali BM. Association of Cu(NO3)2 with Kryptofix-221 in mixed (MeOH-DMF) solvents at different temperatures. American J Fluid Dynam. 2011; 1(1): 4-8.
- Gomaa EA. Solvation parameters of lead acetate in mixed, N,N-dimethylformamide–water mixtures at 298.15K. AnaleleUniversitate din Bucuresti-Chimie. 2010;19: 45-48.
- Handbook of Chemistry and Physics. 91st ed. 2010–2011.
- Marcus Y. “Ion Properties”, Dekker, New York. 1999.
- Marcus Y. “Solvent mixtures”, Dekker, New York. 2005.
- Kim JI, Brückl. On the temperature dependence of solubilities of inert Gases from the scaled particle theory. Z PhysChemNeueFolge. 1978; 110: 197-208.
- Tawa GJ, Topol IA, Burt SK, Caldwell RA, RashinAA.Calculation of the aqueous solvation free energy of the proton. J Chem Phys. 1998; 109: 4852 .
- Camaioni DM, Scherdtfeger CA. J PhysChem A 2005p 109: 10795.
- Casey PK, Christopher JC, Donald GT. Aqueous Solvation Free Energies of Ions and Ion-Water Clusters Based on an Accurate Value for the Absolute Aqueous Solvation Free Energy of the Proton. J PhysChem B. 2006; 110: 16066-16081.
- Shen C, Hagiwara R, Mallouk TE, Bartlett N. Thermodynamic Aspects of the Remarkable Oxidizing Capabilities of Fluorine-Lewis-Fluoroacid Mixtures. ACS Symposium, Inorganic Fluorine Chemistry Ser. 1994; 555:26-39.
- Kelly CP, Cramer CJ, Truhlar DG. Single-Ion Solvation Free Energies and the Normal Hydrogen Electrode Potential in Methanol, Acetonitrile, and Dimethyl Sulfoxide. J PhysChem B. 2007; 111(2): 408-422.
- GomaaEsam A. Molal solubility, dissociation and solvation parameters for saturated benzoic acid solutions in various solvents. Physics Chem Liq. 2012, 50:279-283.
- GomaaEsam A. Solubility and solvation parameters of barium sulphate in mixed ethanol-water mixtures at 301.15. Int J Mater Chem. 2012, 2(1) :16-18.
- GomaaEsam. Electrical conductance of Cu (NO3)2 with Kryptofix-222 in mixed (MeOH-DMF) solvents at different temperatures. American J Environ Eng. 2012, 2(3) :54-57.
- GomaaEsam A. Thermodynamic and polarization parameters of dibenzo18-crown-6 in mixed methanol-water solvents. American J Poly Sci. 2012;2(3):35-38.
- GomaaEsam A. Solvation parameters for sodium oxalate in mixed ethanol- water solvents at 301.15K. EurChem Bull. 2013;1: 259-261.
- GomaaEsam A. AbouElleefElsayed and Mahmoud EA, Gibbs freeenergies for solvation of KClO3 in mixed DMF-H2O solvents at 301.15. EurChem Bull. 2013;2:732-735.
- GomaaEsam A, AbouElleefElsayed. Thermodynamics of the solvation of lead nitrate in mixed DMF-H2O solvents at 301.15K. American ChemSci J. 2013;3:489-499.
- GomaaEsam A, AbouElleefElsayed. Thermodynamics of the solvation of potassium thiocyanateinmixed DMF-H2O solvents at 301.15K. Sci Technol. 2013;3:118-122.
- GomaaEsam A, AbouElleefElsayed, Abdel RazekMG.Thermodynamics of the solvation of CaSO4 in mixed DMF-H2O solvents at 301.15K. Int Res J Pure App Chem. 2013;3:320-329.
- GomaaEsam A. The microscopic free energies of solvation for K+,Rb+ and Cs+ in mixed DMFA-water solvents at 298.15K, Int J TheorMathem Phys. 2013;3:151-154.
- GomaaEsam A, Al Jahadali BA. Conductometric studies of calcium ions With Kryptofix 221 in mixed MeOH-DMF solvents at different temperatures. Education. 2012;2(3)37-40.
- GomaaEsam A. Molal solubility, dissociation and solvation param- teres for saturated phenylalanine in various solvents at 298.15K. American J Biochem. 2012;2(3):25-28.
- GomaaEsam A. Molal solubility, dissocation ,association and solvation parameters for saturated o-chlorobenzoic acid in various solvents at 298.15K. Food Public Health. 2012;2(3):65-68.
- GomaaEsam A. Ionic Gibbs free energies,enthalpies and entropies of some ions in various solvents. Global Adv Res J Chem Mater Sci. 2012;1:35-38.
- GomaaEsam A. The macroscopic and microscopic free energies of solvation of silver chromate and silver phosphate in some organic solvents at 298.15K. Frontiers Sci. 2012;2:24-27.
- GomaaEsam A, AbouElleefElsayed M, Helmy ET, DefrawySh M, Solvent effects on the thermodynamics of solvation of barium diphenylaminesulfonate. Southern J Chem. 2013;21:1-10.
- Gomaa EA , Ibrahim KM, Hassan NM. Conductometric study of complex formation between Cu(II) ion and 2-hyroxyimino-3-(2,-hydrazonopyridyl)-butane(HL). Frontiers Sci. 2012; 76-85.
- Gomaa EA, Ibrahim KM, Hassan NM. Evaluation of thermodynamic parameters (conductometrically) for interaction of Cu(II) ion with 4-phenyl-1-diacetyl monoxime-3-thiosemicarbazone (BMPTS) in (60%V) ethanol water (EtOH-H2O) at different temperatures. The Int J Eng Sci. 2014, 3:44-51.
- Gomaa EA, Abu El-Nader HM, RashedShE. Gibbs free energies for Interaction of CuCl2 with(E)-1-phenyl-2-92-94-9e0-phenyldiazenyl) Phenylhrazono)-2-(phenylsulfonyl) ethanone in ethanol at different Temperatures. The Int J Eng Sci. 2014;3: 64-73.
- Gomaa EA, Ibrahim KM, Hassan NM. Thermodynamics of complex Forrmation (conductometrically) betweenCu(II) ion and 4-phenyl-1-diacet- yl monoxime-3-thiosemicarbazonein ethanol at different temperatures. Research and Reviews: Journal of Chemistry. 2014;3:47-55.
- GomaaEsam A, AbouElleefElsayed M. Thermodynamics of solvation of barium diphenylaminesulfonate in ethanol-water mixed solvents. Thermal Power Eng. 2014;3 : 222-226.
- GomaaEsam A, AbouElleefElsayedM,Elsayed T. HelmyElsayed T. Solvation of oxytetracycline hydrochloride in ethanol-water mixed solvents. Research and Reviews: Journal of Chemistry. 2014;3:22-27.
- GomaaEsam A. Dissociation,association and solvation parameters for Saturated glycine in various solvents at 298.15K. Sci Technol. 2013,3:123-126.
- GomaaEsam A. Thermodynamics of complex formation between Cu(II) and 4-phenyl-1-diacetyl monooxime-3-thiosemicarbazone in methanol. Research and Reviews: Journal of Chemistry. 2014; 3:28-37.
- Gomaa EA, El-Askalany AH, Moussa MNH. Dissociation of KClin mixed hexamethylphosphortriamide-water solvents. Rev RoumChim. 1987;32 :243.
- GomaaEsam A. Theoretical contribution of solvation of AgBr in some organic solvents at 25oC. ThermochimicaActa. 1988,128:99.
- GomaaEsam A. Solubility of tetraphenyl derivatives in aqueous- hexamethylphosphortriamide solutions at 25oC. Indian J Tech.1986;24:725.
- GomaaEsam A. Transfer free energies of ions from water to N,N,- dimethylformamide and its aqueous mixtures based on Ph4AsBPh4 and Ph4SbBPh4 assumptions. Thermochimica Acta.1989;142:19.
- GomaaEsam A. Solvation free energies of K+,Rb+ and Cs+ ions in methanol-DMF mixtures. CroaticaChimicaActa. 1989, 62:475.
- GomaaEsam A. Single ion free energies of some monovalent ions in mixed dimethylacetamide using the asymmetric Ph4AsBPh4 assumption. ThermochimicaActa. 1989;147:313.
- Gomaa EA, Shallapy AM, Moussa MNH. Solute –solvent interaction of phenylalanine in various organic solvents. J Indian Chem Soc.1991;68:339.
- Gomaa EA, Shallapy AM and Moussa MNH, Solvation of o- and p-nitoanilines in some organic solvents. Asian J Chem.1992;4:518.
- Abu El-Nader HM and GomaaEA,Solvation of AgCl in mixed water- DMF solvents. Mansoura Sci Bull. (A Chem).1996;23 :1.
- Kim JI, Cecal A., Born H.J., and Gomaa EA. Preferential solvation of single ion : a critical study ofthe Ph4AsBPh4 assumption for single ion thermodynamics in mixed aqueous-acetonitrile and aqueous-dimethyl formamide solvents. Z Physik Chemic NeueFolge. 1978;110: 209.
- Kim JI, Gomaa EA. Preferential solvation of single ion : The Ph4AsPh4B assumption for single ion thermodynamics in mixed dimethylsulphoxide-water solvents. Bull SocChim Belg.1981;90:391.
- Gomaa EA, El-Khouly AA, Mousa MA. Association of salicylic acid in acetonitrile – water media, Indian J Chem. 1984;23:1033.
- Gomaa EA, Mousa MA, El-KhoulyAA,Gibbs free energies of solute- solvent interactions for salicylic,sulphosalicylic and sulphanilic acids in various solvents. ThermochimicaActa. 1985;86 :351.
- Gomaa EA, Mousa MA, El-Khouly AA. Association, dissociation and hydrogen bonding of salicylic acid in water-N,N-dimethylformamide mixtures. ThermochimicaActa. 1985;89:133.
- GomaaEsamA,Single ion thermodynamics for Cl-, Br- , I-, Ph4B-, K+, Rb+ Cs+ and Ph4As+ in mixed hexamethylphosphortriamide-water Solvents. ThermochimicaActa. 1985;91:235.
- GomaaEsam A. Study of Ph4SbBPh4 assumption for single ion free energies in some organic solvents. Thermochimica Acta.1989;140:7.
- GomaaEsam A. Study of the asymmetric Ph4AsBPh4 assumption for the evaluation of single ion free energies in mixed N-methylpyrrolidone-water solvents. Bull SocChim Fr. 1989;5:620.
- GomaaEsam A. Preferential solvation of Ph4AsBPh4 and Ph4SbBPh4 in mixed DMSO/DMF solvents. Bull Soc ChimFr.1989;5:623.
- GomaaEsam A. Free energies of transfer for some monovalent ions and Ph4SbBPh4 from water to acetonitrile-water mixtures using the asymmetric Ph4AsBPh4 assumption. ThermochimicaActa. 1989,152:371.
- GomaaEsam A. The polarographicelectroreduction of uranyl ion in arsenic Acid solution. MonatisheheftefürChemie. 1988;119:287.
- Shehatta IS, El-Askalany AH, Gomaa EA. Thermodynamic parameters of transfer and solution of oxalic acid in dimethylsulphoxide- water media. ThermochimicaActa. 1993;219:65.
- EA Gomaa, G Begheit. Polarographic and conductometric studies of uranyl ion in sulphuric acid-ethanol media. Asian J Chem. 1990;2:444.
- El-Khouly AA, Gomaa, EA, and Abou-El-Leef S, Conductivity and Solubility studies of (Cd-Kryptofix-22) complexes in various hydooganic solvents. Bull Electrochem. 2003;19:153.
- Hamada MA, Gomaa EA, El-Shishtawi NA. Optomechanical properties of 10% PVA in presence ofCoCl2 and 44% ethanol-water composition. Int J Optoelectronic Eng. 2012;1:1-3.
- Ibrahim Kamal M, GomaaEsam A, Zaky Rania R, Abdel El-Hady MN. The association and formation constants for CuCl2 stoichiometric complexes with (E)-3-oxo-N-(thiazol-2-yl)propanamide in absolute ethanol solution. American J Chem. 2012,2:23-26.
- El-Khouly AA , Gomaa EA and Salem SE. Conductometric study of complex formation between 2,3 –pyrazinedicarboxylic acid and some transition metal ions in methanol. Southern Brazilian J Chem. 2012;20:43-50.
- Gomaa EA and Al –Jahdali BAM. Electrical conductance of Cu(NO3)2 with Kryptofix-222 in mixed (MeOH-DMF) solvents at different temperatures. American J Environ Eng. 2012;2:6-12.
- Gomaa EA, El-Askalany AH, Moussa MNH. Polarographicelectroreduction of uranyl on in glycine,Dl-Aspartic acid and phenylalanine. Asian J Chem. 1992;4:553.
- GomaaEsam A. Application of the scaled particle theory for the solvation of silver tetraphenyl boride in dimethylformamide-water mixtures at 298.15K. J King Saud Uni. 1991;3(1):69.
- GomaaEsam A. Excess volumes aandexess dielectric constant of the mixed solvents : MeOH-DMF,MeOH-DMSO ,DMSO-DMF. Oriental J Chem.1990;6:12.
- Gomaa EA, Hamada MA and Galal R. Apparent molal volumes of sodium fluoride in mixed aqueous-ethanol solvents. Avances en Quimica. 2010;5(2):117-121.
- GomaaEsam A. Solvation parameters of lead acetate in mixed N,N-dimethylformamide mixtures at 298.15K,Analele Uni.dinBucuresti-Chimie. 2010;19(1):45-48.
- El-ShishtawiNagah A, Hamada Maany A, GomaaEsam A. Influence of permanent magnet on the association constants of FeCl3+ 10% PVA in 50% ethanol-water solutions ,conducometrically
- at 298.15K.Phys Chem. 2011;1(1):14-16.
- Gomaa EA and Al Jahdali BAM. Condutometric studies of ionic association of divalent electrolyte Cu(NO3)2 with Kryptofix-22 in mixed MeOH-DMF solutions at different temperatures. American J Condenesed Matter Physics. 2012;2(1):16-21.