ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
Abhishek Singh1, Ashish Raman2, Deepti kakkar3
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
This paper illustrates the results of the throughput of Secondary User (SU) in cognitive radios under cooperative scenario with the use of evolutionary algorithms in the presence of additive white Gaussian (AWGN) noise. In this work, the performance of half-voting and OR fusion rule is studied in terms of Pd Vs Pf curves. OR fusion rule is found to be most suitable in cooperative scenario. Then, Particle Swarm Optimization (PSO) and Biogeography Based Optimization (BBO) algorithms are implemented using OR fusion rule to enhance the throughput of cognitive users by taking in to account the protection of primary (licensed) users. The probability of detection is set to 0.9 for protection purpose. Simulations results in terms of co-operations shows that PSO performs better initially but as numbers of co-operations increases PSO performance degrades.
Keywords |
| Throughput, Evolutionary Algorithms, Fusion rules, Optimization |
INTRODUCTION |
| In recent years, cognitive radio (CR) has emerged as a promising paradigm for exploiting the spectrum opportunity, which is restricted by the current rigid spectrum allocation scheme, to solve the spectrum scarcity problem [1-2]. Different spectrum sensing techniques are available for sensing primary users (PUs) signals. They can be broadly classified in to three categories: matched filter detection, cyclostationary detection and energy detection [19]. Energy detection is widely adopted because of lower complexity than other two schemes and priori knowledge of signal is also not required. Spectrum sensing depends upon two probabilities namely detection probability (Pd) and false alarm probability (Pf) [5]. Detection probability is related to probability of correctly detecting the presence of PUs, whereas false alarm probability is related to incorrect detection of PUs when it is absent [4]. Many research works are proposed to improve the performance metrics of detection probability and false alarm probability. However, PSO is addressed for sensing-throughput trade-offs problem under cooperative scenarios using various hard combination fusion schemes [3]. Optimization performance of cooperative sensing in terms of number of cooperative users is performed using constant detection rate (CDR) and constant false alarm rate [4]. But, there is no consideration for throughput of CUs. The work in [5] focuses on the optimization of sensing-throughput tradeoffs using iterative algorithms. In this paper, PSO and BBO algorithms are implemented to achieve the same objective. Both the algorithms are performed over OR fusion schemes. |
| The Paper is organized as follows: Section-II denotes the system model and other performance metrics. A BBO and PSO algorithms are discussed in section III and IV respectively. Section 5 covers the methodology used by proposed work. However, the section VI and section VII include results and conclusions respectively. |
II.SYSTEM MODEL |
| This study focuses on PUs signals with AWGN at CUs. We assume that both noise and PUs signal are independent. The basic model for energy detector shown in fig 1, consists of noise filter, square law device and integrator as [6]; |
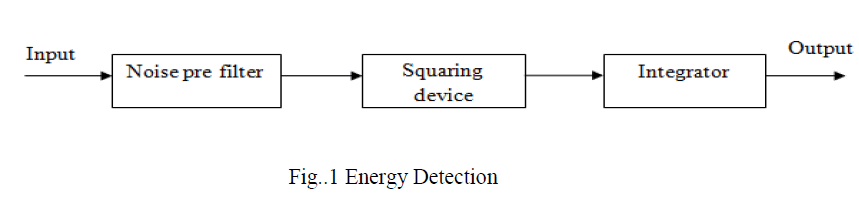 |
| The output signal is compared against a particular threshold to decide whether the signal is present or not. Threshold is decided depending upon statistical properties of Output(O/p). In the cooperative detection, secondary users receive the transmitted signals and calculate signal/energy power. After performing detection, individual hard decisions are sent to a fusion centre for decision combining using some fusion rules. The Pf is related to Pd, number of observation samples (N) and SNR (ïÿýïÿý) as follows [5]; |
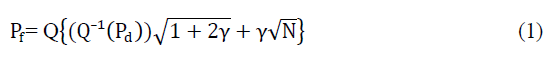 |
| The number of observation samples for sensing is related to Pd and Pf [5] under energy detection by: |
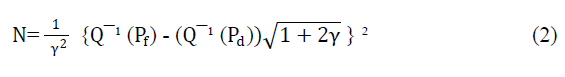 |
| The cooperative model taken into consideration is shown in Fig.2 [18]; |
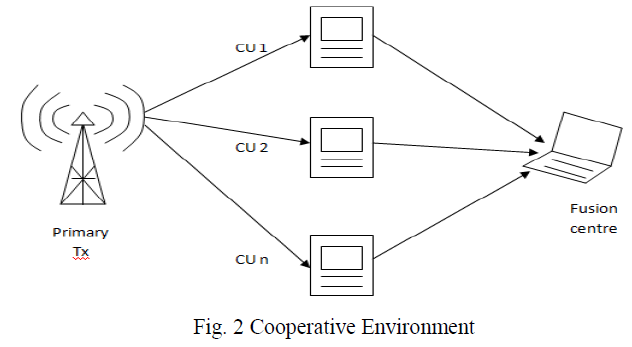 |
| In fig.2, CU1, CU2, ……. CUN are cognitive users providing individual sensing decisions which are then combined at the fusion centre using various fusion rules such as OR, AND, and Half-voting. |
| A.Hard decision fusion rules |
| The fusion centre implements n-out-of-M rule if at least n local decisions indicate the presence of PUs. The probability of detection at fusion centre assuming uncorrelated decisions is given by [6-7] |
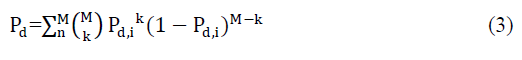 |
| 1) Logical and-rule |
| In this rule, if all the decisions sent to the fusion centre are one, then the final decision made by the combiner is one. The performance evaluation using this fusion rule is computed by setting n=M in above equation as [6]; |
 |
 |
| Fig.3 describes that a frame duration is divided in to two phases: Sensing phase and transmission phase. The transmission phase contributes to the throughput of cognitive users. |
| The throughput of the CUs is generated under two conditions, as reported in [8]: First scenario indicates the absence of PU signal and no false alarm is generated by CU. The throughput in this case is given by [3]; |
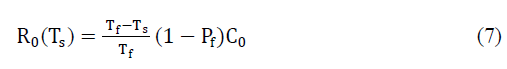 |
| Second scenario states that PU is not detected by CU even if it is present. The throughput for this case is as follows [3]; |
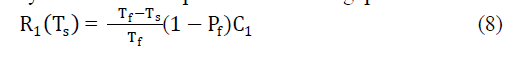 |
| C0 âÃËödenotes throughput of CU in PU absence C1:denotes throughput of CU operating in the presence of PU |
| The net achievable throughput of the system is represented as [9]; |
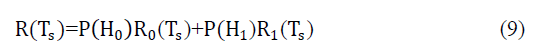 |
| Where P(H1) is the probability of PU being active and P H0 = 1 − P(H1) |
| The problem criterion can be fixed as follows: To maximize the value R(Ts) above such that Pd never goes below 0.9 for PU protection, numerically it can be shown as; |
| max R(Ts) such that Pd>0.9 wrt FCC guidelines |
| Assuming P(H1) considerably small<0.2 [9] and C0 > C1, eqn. (9) simplifies to |
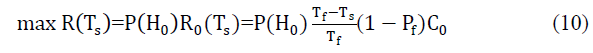 |
III.BIO-GEOGRAPHY BASED OPTIMIZATION |
| Biogeography-Based Optimization (BBO) is a global optimization algorithm developed by Dan Simon in 2008 and is inspired by mathematical models of biogeography by Robert MacArthur and Edward Wilson. Biogeography is the study of distribution of species in nature over time and space; that is the immigration and emigration of species between habitats [16]. Each possible solution is an island and their features that characterize habitability are called suitability index variables (SIV) [21]. The fitness of each solution is called its habitat suitability index (HSI) and depends on many features of the habitat. High-HSI solutions tend to share their features with low-HSI solutions by emigrating solution features to other habitats. Low-HSI solutions accept a lot of new features from high-HSI solutions by immigration from other habitats [20]. |
| A. BBO operators |
| Migration: The BBO migration strategy in which we decide whether to migrate from one region to other or not [22]. The migration rates of each solution are used to probabilistically share features between solutions. BBO migration is used to change existing habitat. Migration in BBO is an adaptive process [16]. |
| Mutation: Mutation is a probabilistic operator the randomly modifies a solution feature. The purpose of mutation is to increase habitat among the population [21]. For low value solutions, mutation gives them a chance of enhancing the quality of solutions, and for high fitness value solutions, mutation try to improve the value as compared to the previous value [20]. |
| B. Limitations of GA over BBO: |
| 1) Genetic algorithms cannot ensure finding a global optimum; they usually give a good approximation [13]. |
| 2) Genetic algorithms can take a long time to converge and are also not easy to implement [17]. |
| 3) Genetic algorithms do not scale well with complexity [15]. That is, where the number of elements which are exposed to mutation is large there is often an exponential increase in search space size. |
IV.PARTICLE SWARM OPTIMIZATION |
| PSO is an evolutionary algorithm which is population based and designed keeping in view the social behavior of flock of birds [10-11]. Each solution is represented by a particle and the particles are grouped into swarm. Each particle moves toward best optimal solutions with every iterations by learning from past experiences and surroundings. Due to its simplicity, high convergence rate, and searching capability, PSO has been deployed to many optimization problems [12]. After achieving the required output or number of iterations, process terminates. |
| Two fundamental equations which are the essence of PSO representing position and velocity of the particle at any instant t+1 are [10] |
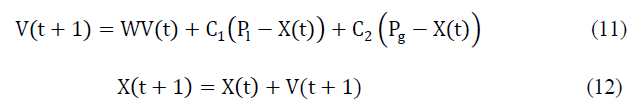 |
| where ïÿýïÿýïÿýïÿý and ïÿýïÿýïÿýïÿý are local best of particle and global best of the swarm respectively. |
| For a particle with n-dimensions, vector X and vector V can be represented as X=(x1, x2, . , xn), V=(v1, v2, … , vn) and P=(p1, p2, … . . , pn). V(t) ensures that all the particles are in the right direction without any sudden change whereas 2nd and 3rd terms in eqn. (11) measures the performance of particle relative to its past performance and neighbor performance |
METHODOLOGY |
| The basic optimization flow using BBO and PSO algorithm is as follows: Firstly, the performances of decision fusion rules such as OR and Half-Voting are compared in terms of their Pd Vs Pf plots. The rule with better system performance i.e. smaller value of Pf and larger value of Pd is then used in the optimization environment to optimize the throughput (T) of SUs. The optimization parameters for both PSO and BBO such as swarm size, mutation probability, weight factors, and learning factors are defined. Then solutions are randomly initialized for BBO with random positions and zero initial velocities in case of PSO. Based on the migration rate, the features of solutions are updated and mutation if desired is applied in BBO. The positions of particles are updated in terms of velocity vectors in PSO. This process continues until the desired output or termination condition is achieved. Finally, the results are compared to conclude the performances of both evolutionary algorithms. |
 |
| The value of parameters used for BBO and PSO algorithm are indicated in table 1 and table 2 respectively. These values are used for designing the framework of optimization process. |
VI.RESULTS AND DISCUSSIONS |
| Based on the boundary condition given in table 1 and 2, all the simulation has been performed on MATLAB under nakagami-m fading environment with AWGN, with Pf<=0.3 and Pd=0.9. Using the formula for OR fusion rule as given in equation (5), simulation is carried out. |
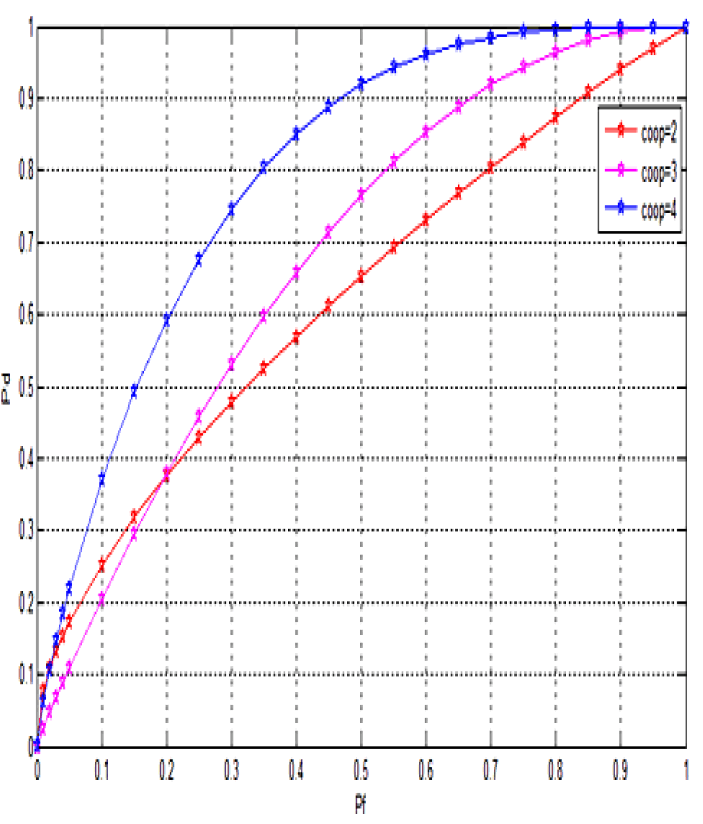
| Fig.5. shows the Pd Vs Pf curve for AWGN channel with half voting Fusion rule for different number of co-operations (2, 3 and 4). |
| Fig.6. shows the Pd Vs Pf curve for AWGN channel with OR Fusion rule for different number of co-operations. |
 |
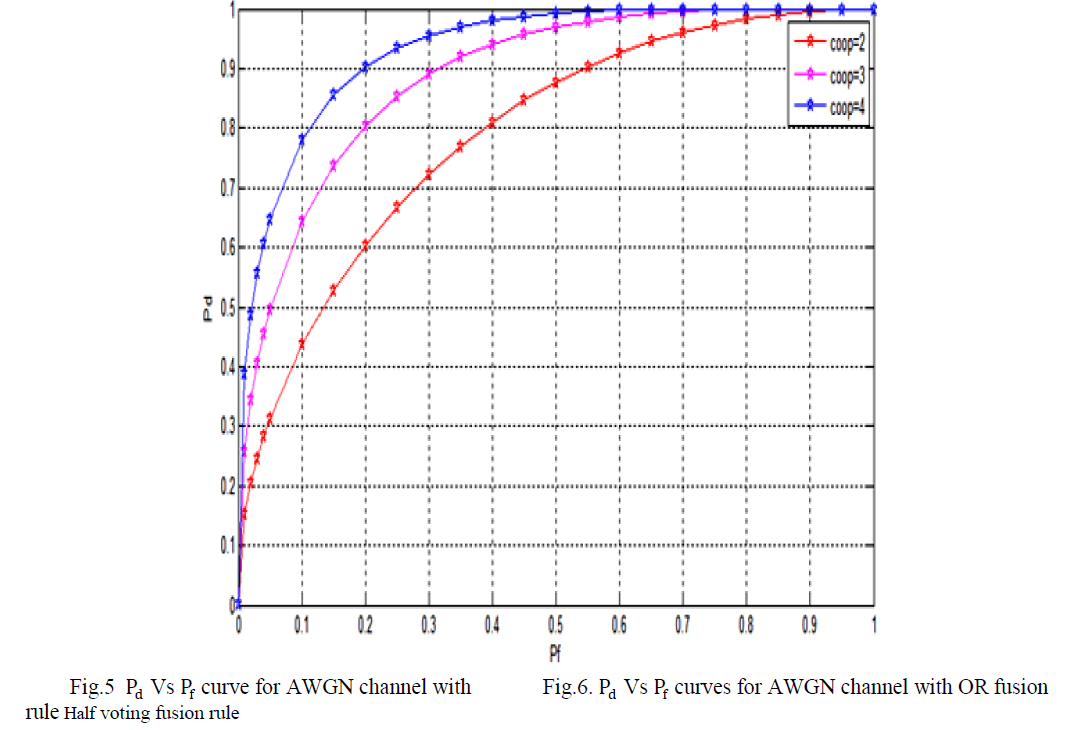 |
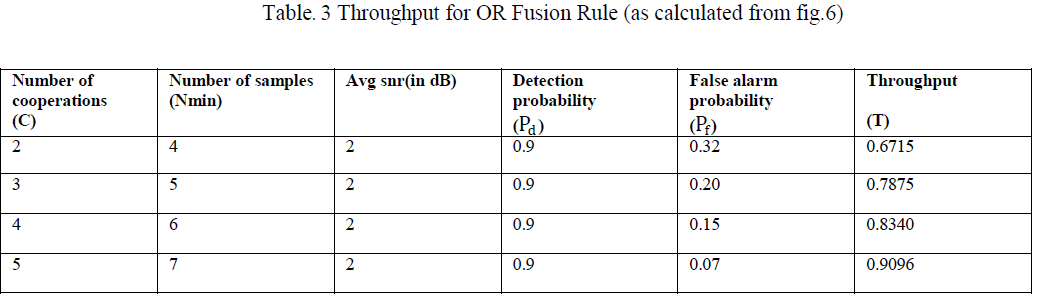
| From fig.5 and fig.6, it is seen that ROC curves for both fusion rules shift toward left side with increase in number of cooperation indicating an improvement in system performance. But the shift in case of OR fusion rule is more as compared to half-voting rule. For 4 cooperation case, targeted detection probability (Pd) of 0.9 is achieved at Pf=0.2 in case of OR fusion rule and at Pf=0.45 in case of half-voting rule. A smaller value of Pf denotes that OR fusion rule is more suitable as compared to Half-Voting rule. The table.3 is formed using eqn. (2) and (10). The value of throughput for OR fusion rule with different number of cooperation is shown in table 3. |
 |
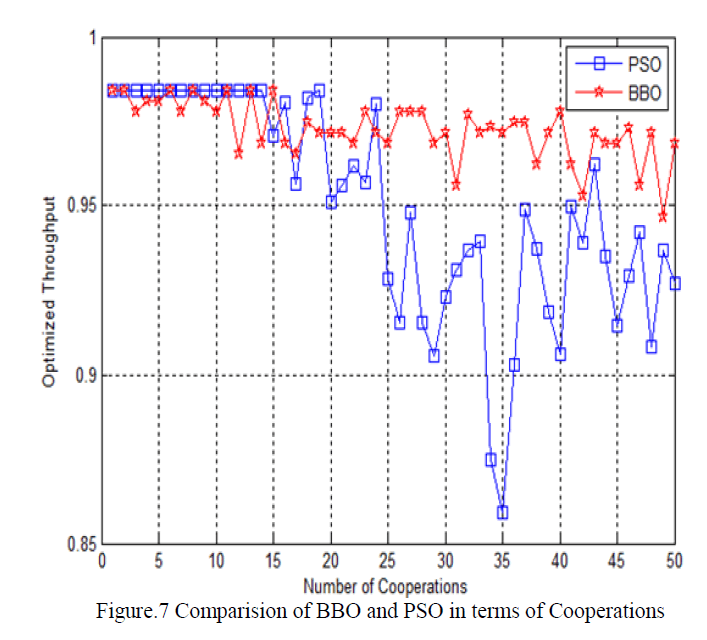 |
| Fig.7 shows the throughput of the SUs with respect to cooperation for both PSO and BBO. Simulation results shows that both optimization algorithms provides better results as compared to non-optimized throughput values as given in table 3. There is an improvement of 8% in SU throughput for 4 cooperations. Among BBO and PSO, PSO is dominant initially but its performance deteriorates as the number of cooperations increases. |
VII.CONCLUSION |
| With the help of this paper, we study the performance of the BBO and PSO algorithms for throughput optimization of the cognitive users in cooperative scenario case using OR fusion rule and comes at the conclusion that these evolutionary algorithms perform better than non-optimized (normal) case and results in higher achievable throughput. The performance of the PSO algorithm in terms of number of co-operations is dominant initially but as the number of co-operations increases, BBO performance remains steady whereas PSO performance degrades. |
References |
|