Transformed Chaotic Signals with Lyapunov Spectrum for Quantitative Measure of Its Sensitivity to Initial Conditions

Abstract

The purpose of this paper is to consider a class of recursively defined signals that exhibit complex dynamics in phase space. This work arose out of an interesting radar signal. This signal exhibits sensitive dependence on initial conditions, and has an unusual self replicating feature in phase space. The main issue to be addressed in this paper is whether such signals are of practical use in radar. Signals are of paramount importance in radar. Radar systems use different types of signals for specific applications in varying situational contexts.

Keywords

Chaos, Lyapunov Signal, Initial condition, Radar.

Introduction

There are hence many different classes of radar signals. Chaos theory is the analysis of the behavior of such systems. As such, chaos theory is not really a theory of chaos, but is more concerned with understanding the complex behavior of nonlinear dynamical systems. We will introduce briefly the study of such systems, and in particular, will be interested in determining under what conditions such a system becomes chaotic. A class of radar signals will be introduced. We will investigate one signal in this class, and apply the ambiguity function to see whether they are of practical use in radar. This note introduced a class of recursively defined signals, motivated from [1]. Their stability was analyzed using a Lyapunov spectrum. These signals are members of a class of irregular/noise like signals described in [2]. This note is a preliminary study of radar signals viewed as discretised nonlinear dynamical systems. A class of recursively defined signals is introduced, and one specific signal is considered. It will be shown that such signals can exhibit complex dynamics in phase space. Based upon the shape of the absolute value of their ambiguity functions, we can conclude that they should have an ability to resolve targets in both time delay and Doppler shift. The disadvantage of such signals is that they have relatively high range and Doppler side lobes in the ambiguity diagram, which will limit their ability to discriminate small targets against clutter, and small targets in the vicinity of larger targets.

Lyapunov Spectrum

Lyapunov exponents of a dynamical system provide a quantitative measure of its sensitivity to initial conditions. The Lyapunov spectrum of a map is a plot of its Lyapunov exponents. As pointed out in [3], they give the average rate of convergence or divergence of the system along the principal axes in phase space. The existence of at least one positive Lyapunov exponent is a necessary condition for a dynamical system to be chaotic [4]. Hence, given a dynamical system, if we can establish that there is at least one positive Lyapunov exponent, then we can be certain the system will exhibit chaotic dynamics. For a dynamical system, where we know the generator φ , it has been shown that the complete Lyapunov spectrum can be easily computed [5]. This can be done by considering the perturbation of a point of the system, and applying a linear stability analysis [5].We focus on the calculation of Lyapunov exponents in the current context of one-dimensional discrete maps. The ideas to follow can be found in [3,4]. Consider the dynamical system (Eq.1), with initial condition x(0) Further details can be found in [4-5]. It is clear from (Eq.1) that μ depends on the starting point x(0). For a given attractor, μ is invariant in the basin of attraction [5]. Simulation tests of a small perturbation of this starting point, defined by x(0) + δ(0), where the initial separation δ(0) is assumed to be very small. Suppose δ(n) is the separation after n iterations of the system. 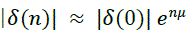then μ is called a Lyapunov exponent. These can be found, for a trajectory starting at x(0), from the limit

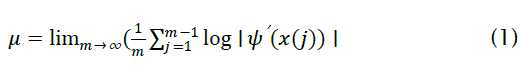
If a Lyapunov exponent is negative for a particular orbit, then the orbit either has a stable fixed point, or a stable limit cycle. In the case where it is positive, the orbit is in a strange attractor, and the trajectory will be chaotic. Fig.1 is a plot of the Lyapunov spectrum for the Logistic map introduced previously, with x(0) = 0.1. As can be observed, the map has stable dynamics until at approximately λ = 3.6, where it becomes chaotic, followed by periods of stability and then chaos. In the current context of radar signals in the class C_D we can calculate the Lyapunov spectrum, and use it to decide which parameter values generate a chaotic signal.

Figure 1: A plot of the Lyapunov spectrum for the logistic map

Chaotic Signal Analysis

The is chaotic signal that with generator φ(x,λ) = λ sin (2πx). To illustrate the sensitivity of the corresponding signal, defined through (Eq.2), to initial conditions, consider Fig.2. This is a plot of the differences of two versions of (Eq.2). We denote these two signals as x(n) and y(n) respectively. One has initial value x(0) = 2 , while the second starts with y(0) = 2 + 10^-12 In both cases, λ = 2 . The plots in Fig.2 show the original signal x(n), the perturbed signal y(n) and their pointwise differences x(n) - y(n). It would not be unreasonable to assume that these signals would evolve almost identically, given the difference in initial values is 10⁻¹². Fig.2 shows that they do initially, but there is then a divergence apart. As pointed out previously, such behaviour is characteristic of a chaotic system.

Figure 2: Plots of signals with generator . The first plot shows an orbit starting with x(0) = 2, while the second shows an orbit perturbed by a factor of 10^-12 The bottom subplot shows the point wise differences x(n) - y(n) .

Lyapunov spectrum for this signal plot in Fig.3, with λ ranging from 1 to 5. For each value of λ , (Eq.1) is estimated using m=1000, with an initial starting point of x(0 ) =2. This spectrum is invariant in a basin of Due to the shape of the ambiguity functions; the corresponding signal should have an ability to resolve targets in both time delay and Doppler shift. However, it would be expected that such a signal may not provide a radar with a sufficient ability to differentiate targets in clutter with a low Radar Cross Section (RCS), due to the extensive high side-lobe response in the ambiguity function. Since the corresponding signal is in discrete time, the time delay, (τ) axis values are in discrete time units. Better graphical resolution is achieved by extending this axis. The Doppler axis is in units of radians, while the time delay is measured in seconds. The absolute value of the ambiguity function is in a linear scale. The autocorrelation plot is shown over a larger spectrum of values of τ than used in the previous three subplots, and also is in a linear scale.

Figure 3: The Lyapunov spectrum for the signal with generator

Conclusion

This paper described four classes of radar signals, based upon their characteristics and ambiguity functions. Linear frequency modulation, single frequency pulse trains, step frequency continuous waves, step frequency pulse trains, pseudorandom codes and random noise are examples pointed out in details. A relatively new class of signals is those which have chaotic dynamics. Such a class of signals exhibits a phenomenon known as sensitive dependence on initial conditions. This means that they experience sensitive dependence on initial conditions. Using the Lyapunov spectrum, we determined the stability of this signal. We also investigated whether such signal is of practical use in radar by examining its ambiguity functions.

References

1. Haykin S, Li XB. Detection of Signals in Chaos. IEEE Proc. 2005;83:95-122.
2. Haykin S, Puthusserypady S. Chaotic Dynamics of Sea Clutter. (Wiley, New York), 1999.
3. Benettin G, Galgani L, Giorgilli, Strelcyn J. Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems; a method for computing all of them. Part I, II. Meccanica, 15, 9—30, 2010.
4. Wu X, Liu W, Zhao L, Fu J. Chaotic Phase Code for Radar Pulse Compression. Proceed. IEEE Radar Conf., 279-283, 2011.
5. Li TY, Yorke JA. Period Three Implies Chaos. Amer Math. 2009;82.