ISSN ONLINE(2319-8753)PRINT(2347-6710)
ISSN ONLINE(2319-8753)PRINT(2347-6710)
Rajni Gupta1, Mr. Rinku Kumar2
|
| Related article at Pubmed, Scholar Google |
Visit for more related articles at International Journal of Innovative Research in Science, Engineering and Technology
Wavelet transform can be applied with the Fourier transform to analyse a signal. This transform gives the signal characteristics in time or in frequency domain. But they don‟t give the combination of both. Wavelet Transform splits the signal energy in time-frequency domain. In this paper, In this a new approach was presented in order to recognize and distinguish fault signal from inrush current. With this kind of analysis, these two currents can be separated simply since the distribution of energy in time and frequency domain for inrush and fault currents is very different. The results shows that DCT –DWT splits differential current into small wavelets. This is done by filters in DWT. Various wavelet filters has been tried for all types of faults. It has been concluded that db6 wavelet shows best result for fault detection.
Keywords |
| Discrete Cosine Transform, Discrete Wavelet Transform, Inrush Current, db6 wavelet |
INTRODUCTION |
| Transformers are an essential part of the electric power system because it has ability to change voltage and current level, which enables to generates, transmit and distribute electric power at economical and suitable level. Figure shows that voltage of electricity generated at the power plant will be increased at higher level by using step-up transformers. A higher voltage will reduce the energy lost during the transmission process of the electricity. After electricity has been transmitted to various end points of the power grid, voltage of the electricity will be reduced to usable level by using step-down Transformers are a vital component of the electric power system and they are extensively used to help meet the growing energy needs. There are many different types of transformers. For instance, power transformer and distribution transformer are used in electrical power systems. Isolating transformer can be used to electrically isolate circuits from each other or it can isolate the block signal between circuits. Instrument transformer can be used to measure high voltages and high currents. In addition, based on the construction of core transformer are classified into shell type and core type. |
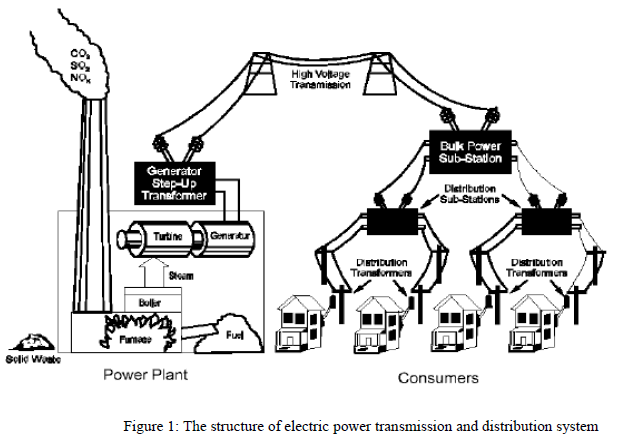 |
| Transformers are a vital component of the electric power system and they are extensively used to help meet the growing energy needs. There are many different types of transformers. For instance, power transformer and distribution transformer are used in electrical power systems. Isolating transformer can be used to electrically isolate circuits from each other or it can isolate the block signal between circuits. Instrument transformer can be used to measure high voltages and high currents. In addition, based on the construction of core transformer are classified into shell type and core type. |
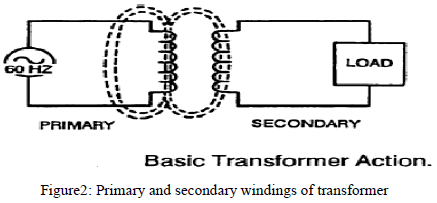 |
| Figure2 shows the basic operating principle of the transformer. The input coil of the transformer is called the primary winding and the output coil is called the secondary winding. The voltage induced in the secondary is determined by the turn ratio and the primary side voltage. |
II. INRUSH MAGNETIZING CURRENT |
| When the transformer is disconnected from its source a magnetizing current is retained in the primary of transformer which causes a high surge of current. This surge is multifold to transformer rating and it exists till all the magnetic flux is removed by supply. Magnetizing Inrush current in transformer results from any abrupt change of the magnetizing voltage. Although usually considered as a result of energizing a transformer. Due to presence of a small resistor and large resistance in the transformer winding an inrush current appear in the primary winding. A. Causes of Inrush Current 1. Occurrence of an external fault 2. Voltage recovery after clearing an external fault. 3. Change of the character of a fault. 4. Out of phase synchronizing of a connected generator. B. Characteristics of Inrush Current ïÃâ÷ Generally contain dc offset, odd harmonics, and even harmonics. ïÃâ÷ Typically composed of unipolar or bipolar pulses, separated by intervals of very low current values. ïÃâ÷ Peak values of unipolar inrush current pulses decrease very slowly. ïÃâ÷ Time constant is typically much greater than that of the exponentially decaying dc offset of fault currents. ïÃâ÷ Second-harmonic content starts with a low value and increases as the inrush current decreases. |
III.FAULT ANALYSIS |
| A. Fourier Transform Fourier transform (FT) is the most popular transformation that can be applied to travelling wave signals to obtain their frequency components appearing in the fault signal. Usually, the information that cannot be readily seen in the time domain can be seen in the frequency domain. The FT and its inverse give a one-to-one relationship between the time domain x(t) and the frequency domain X(w). Given a signal I (t), the FT FT (w) is defined by the following equation: |
 |
| Where 1 < k < N. The FT gives the frequency information of the signal, but it does not tell us when in time these frequency components exist. The information provided by the integral corresponds to all time instances because the integration is done for all time intervals. It means that no matter where in time the frequency f appears, it will affect the result of the integration equally. This is why FT is not suitable for non-stationary signals. The FT has good results in the frequencydomain but very poor results in the time domain. When the current surge hits the fault point, it is reflected with the same sign and travels back to the source end of the line. Then, it is reflected again from the source end with the same sign and returns back to the fault point. Since the duration of this complete cycle is 4 , (τ is the propagation time of the surge from the source end to the fault point) the main component of the current signal after the circuit breaker opening has a frequency equal to |
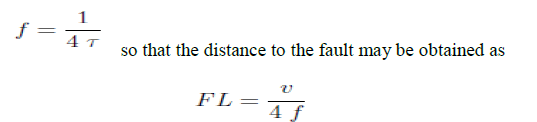 |
B. Discrete Wavelet Transform |
| The wavelet multi resolution analysis is a new and powerful method of signal analysis and is well suited to travelling wave signals. Wavelets can provide multiple resolutions in both time and frequency domains. The windowing of wavelet transform is adjusted automatically for low and high-frequencies i.e., it uses long time intervals for low frequency components and short time intervals for high frequency components. Wavelet analysis is based on the decomposition of a signal into „scalesâÃâ¬ÃŸ using wavelet analysing function called „mother waveletâÃâ¬ÃŸ. The temporal analysis is performed with a contracted, high frequency version of the „mother waveletâÃâ¬ÃŸ, while the frequency analysis is performed with a dilated, low frequency version of the „mother waveletâÃâ¬ÃŸ. Wavelets are functions that satisfy the requirements of both time and frequency localization. The necessary and sufficient condition for wavelets is that it must be oscillatory, must decay quickly to zero and must have an average value of zero. In addition, for the discrete wavelet transform considered here, the wavelets are orthogonal to each other. Wavelet has a digitally implementable counterpart called the discrete wavelet transform (DWT). The generated waveforms are analyzed with wavelet multi resolution analysis to extract sub-band information from the simulated transients. Daubechies wavelets are commonly used in the analysis of travelling waves. They were found to be closely matched to the processed signal, which is of utmost importance in wavelet applications. Daubechies wavelets are more localized i.e., compactly supported in time and hence are good for short and fast transient analysis and provide almost perfect reconstruction. However, there are some other wavelets show a good correlation with the transient signals and may be used in the analysis. Several wavelets have been used in this thesis. Due to the unique feature of providing multiple resolution in both time and frequency by wavelets, the sub-band information can be extracted from the original signal. When applied to faults, these sub-band information are seen to provide useful signatures of transmission line faults, so that the fault location can be done more accurately. By randomly shifting the point of fault on the transmission line, a number of simulations are carried out employing the MATLAB. The generated time domain signals for each case are transferred to the modal domain using ClarkâÃâ¬ÃŸs transformation. Then, the aerial mode signal is analyzed using wavelet transform. From the different decomposed levels, only one level is considered for the analysis. This level has the highest energy level output and the dominant frequency of the transient. Waveforms associated with the travelling waves are typically non-periodic signals that contain localized high frequency oscillations superimposed on the power frequency and its harmonics. DFT was found to be not adequate for decomposing and detecting these kinds of signals because it does not provide any time information. On the other hand, the STFT takes the time dependency of the signal spectrum into account. However, the time-frequency plane cannot give both accurate time and frequency localizations. The Wavelet transform allows time localization of different frequency components of a given signal like the STFT but its transformation functions called wavelets which adjust their time widths to their frequency in such a way that higher frequency wavelets will be narrow and lower frequency ones will be broader. WaveletâÃâ¬ÃŸs time frequency resolution provides a useful tool for decomposing and analyzing fault transient signals. Given a function x(t), its Continuous Wavelet Transform (CWT) is defined as follows: |
 |
 |
| A time-scale representation of a digital signal is obtained using digital filtering techniques. Above figure shows the wavelet transform filter bank. The DWT analyzes the signal at different frequency bands with different resolutions by decomposing the signal into a coarse approximation and detail information. The DWT employs two sets of functions, called wavelet functions and scaling functions, which are associated with a lowpass and high-pass filters. The multi-stage filter bank implement the DWT using the low-pass mother wavelet H1(n) and its half band highpass filter dual, H1(n) . After the filtering, half of the samples can be eliminated according to the NyquistâÃâ¬ÃŸs rule, since the signal now has a highest frequency of f /2 instead of f. The signal therefore can be downsampled by 2, simply by discarding every other sample. The output of the low-pass filter is filtered again in high and low-pass filters until DC value is reached. This procedure is repeated without the down-sampling block after the high-pass filters. H0 and H1 are low-pass and high-pass filters respectively. The outputs of the high-pass filter are the original signal in different scaling. |
IV.PROPOSED METHOD USING DCT-DWT |
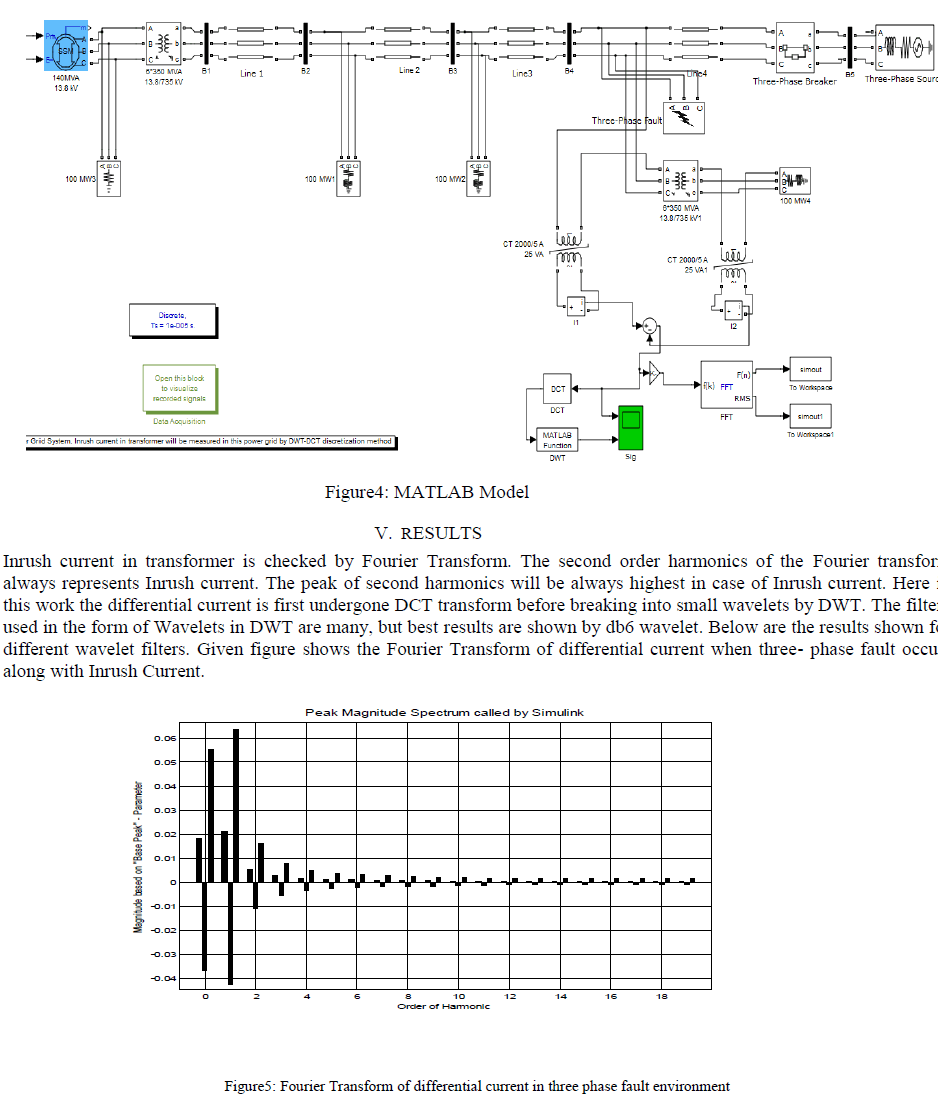
| In this a model is developed in Simulink as shown in figure below. A general transmission line is modelled in sim power tool of MATLAB using 140MVA, 13.6KV voltage source. A transformer is connected in line 4. The current before the transformer and after the transformer is detected by connecting it into phase A. This differential current is then taken ahead for further analysis of fault. Here Fourier transform along with DWT-DCT are used for analysis. Results combining both will be discussed. A MATLAB function block is used here in this model to call the function „dwtâÃâ¬ÃŸ. This function computes the Fourier transform of the differential current. |
 |
 |
 |
VI. CONCLUSION |
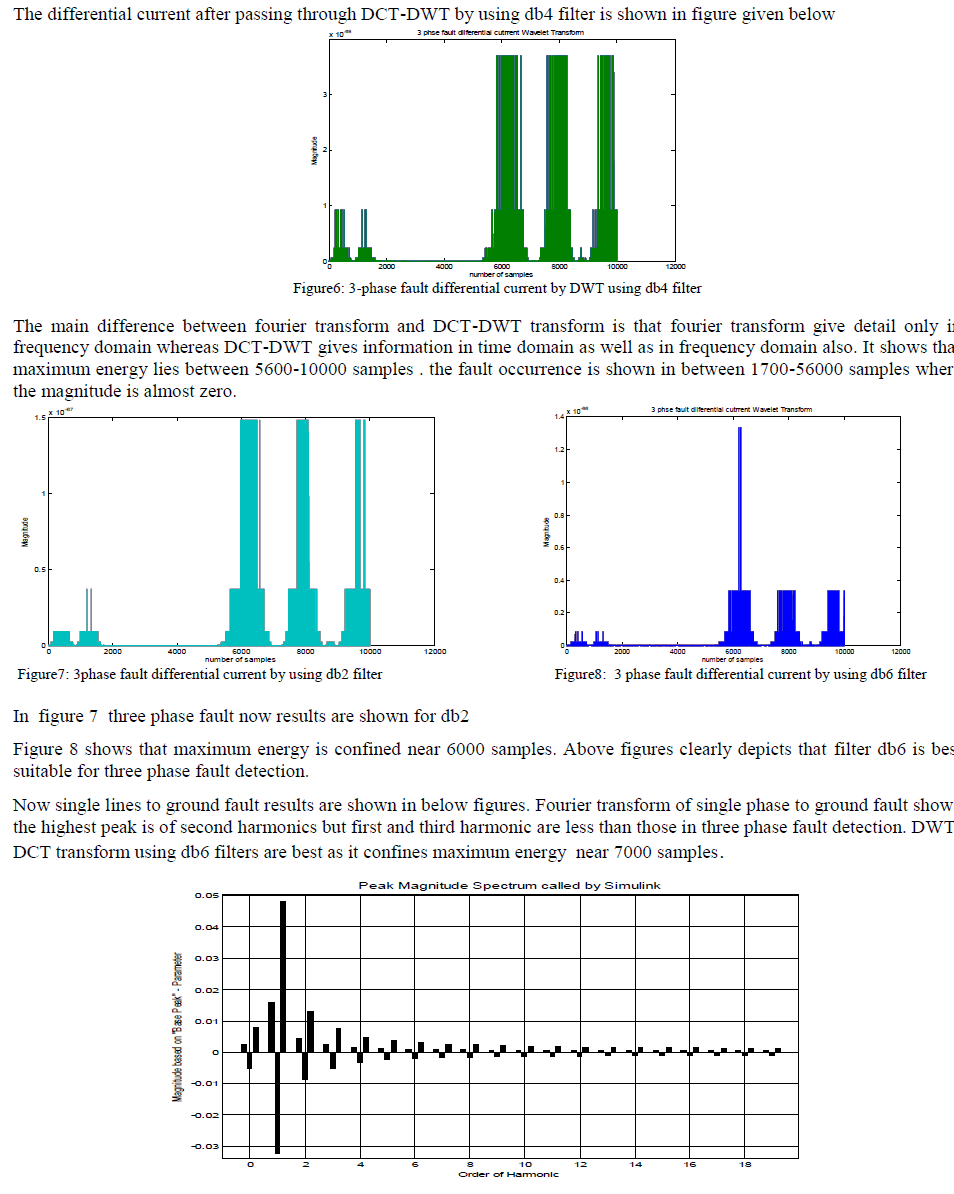
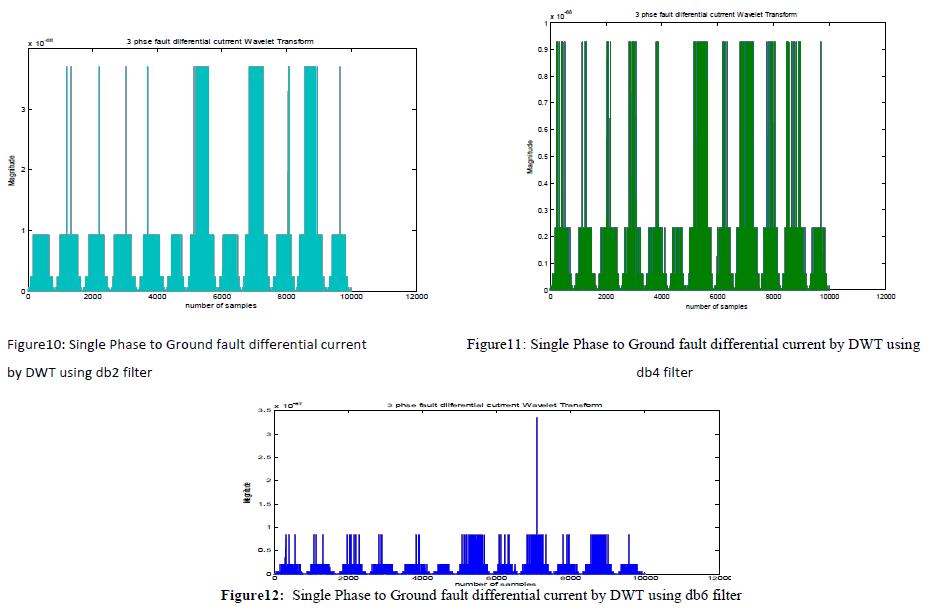
| In this study a new approach was presented in order to recognize and distinguish fault signal from Inrush current. Wavelet transforms splits off the signal energy in time-frequency domain whereas Fourier transformer does not have this capability. With this kind of analysis, these two currents can be separated simply since the distribution of energy in time and frequency domain for inrush and fault current is very different. Because of the existence of DC component and even harmonics in inrush current and regarding the sampling frequency (64 samples per cycle) the energy of zero, third and fourth levels can be a proper criteria for recognition. It has been shown in results that DCT – DWT splits differential current into small wavelets. This is done by filters in DWT. Various wavelet filters has been tried for all types of faults. It has been concluded that db6 wavelet shows best results for fault detection. Results are also shown using Fourier transform. But Fourier transform shows results only in frequency domain. The second harmonic represents the inrush current. DCT-DWT shows that when three phase fault occurs then maximum energy is confined in single lob near 7000 sample while in single phase to ground and double phase to ground the all energy is not confined into single lob it is distributed in other lobs also as cleared from results. |
References |
|