ISSN ONLINE(2278-8875) PRINT (2320-3765)
ISSN ONLINE(2278-8875) PRINT (2320-3765)
R Bhagya1, Dr. A G Ananth2
|
Visit for more related articles at International Journal of Advanced Research in Electrical, Electronics and Instrumentation Engineering
A detail analysis of the performance of 2X2 MIMO (Multiple Input Multiple Output) antenna systems has been carried out for three different types of detectors at the receiver end by determining the transmit diversity using OSTBC multiplexing techniques. The transmission characteristics of the MIMO system have been determined for BPSK, QPSK and 16-QAM modulation schemes presuming Additive White Gaussian Noise (AWGN) and for the flat fading Rayleigh channel. On the receiver side, equalization detection technique are determined by combining Successive Interference Cancellation with Zero Forcing (ZF-SIC), Minimum Mean Square Equalization (MMSE-SIC) and Maximum Likelihood (ML-SIC) has been employed for determining the BER Vs SNR performance of the communication channel. The simulation results show that for BER of ~10-3, the SNR increases with higher modulation schemes from BPSK to 16-QAM. Further the results of the analysis for different detector systems indicate that for BPSK modulation at BER ~10-3 , the SNR values are found to be ~24.46 dB for ZF-SIC, SNR ~20.6 dB for MMSESIC and SNR ~14.46 dB for ML-SIC detectors. Thus the BER performance of 2X2 MIMO-OSTBC transmission channel shows the reduction of SNR ~10 dB for ML detectors. A comparison of the MIMO performance with OSTBC multiplexing techniques indicate that the 2x2 MIMO–OSTBC transmission channel for BPSK modulation depicts better performance for OSTBC multiplexing with ML detector system at the receiving end. The simulations results are presented and discussed in the paper.
Keywords |
| Multiple Input Multiple Output (MIMO), Orthogonal space time block codes (OSTBC), Zero Forcing- Successive Interference Cancellation (ZF-SIC), Minimum Mean Square Equalization-Successive Interference Cancellation (MMSE-SIC), Maximum Likelihood- Successive Interference Cancellation (ML-SIC), Phase Shift Keying(PSK), Quadrature Amplitude modulation (QAM), Bit Error Rate(BER), Signal to Noise Ratio (SNR). |
INTRODUCTION |
| A mobile radio channel is characterized by a multipath fading environment. The signal is offered to the receiver contains not only line of sight of radio wave , but also a large number of reflected radio waves that arrive at the receiver at different times. Delayed signals are the result of reflections from terrain features such as trees, hills, mountains, vehicles or buildings. These reflected delayed waves interfere with direct waves and cause Inter Symbol Interference (ISI) which causes significant degradation of network performance. MIMO technology has attracted attention in wireless communications, because it offers significant increases in data throughput and link range without additional bandwidth or transmit power. It achieves this by higher spectral efficiency and link reliability or diversity (reduced fading). Because of these properties, MIMO is an important part of modern wireless communication standards such as IEEE 802.11n (Wi-Fi), 4G, 3GPP Long Term Evolution and WiMAX [1, 2 ,3]. OSTBCs are attractive techniques for MIMO wireless communications. They exploit full spatial diversity order and employ symbol-wise decoding such as ZF, MMSE and ML. MIMO-OSTBC with detectors is used to reduce complexity and noise in flat fading Rayleigh channels. MIMO techniques offer the promise of high spectral efficiency and robustness to fading. Key to their success is the MIMO detector at the receiver, whose job is to recover the symbols that are transmitted simultaneously from multiple antennas. ZF receiver which implements matrix (pseudo)-inverse (ignores noise enhancement problems) and MMSE receiver optimizes the noise and offers a compromise between residual interference between input signals and noise enhancement. ML is exhaustive optimum detection receiver uses complexity exponential in QAM. In diversity methods a single stream is transmitted but the signal is coded using techniques called Space Time Code. The signal is emitted from each of the transmit antennas using certain principles of full or near orthogonal coding. Diversity exploits the independent fading in the multiple antenna links to enhance signal diversity Space Time Code. Redundant data sent over time space domains (antennas) and the receive SNR increases for different digital modulation schemes. STBCs as originally introduced and studied are orthogonal. This means that the STBC is designed such that the vectors representing any pair of columns taken from the coding matrix are orthogonal. The result of this is simple, linear, optimal decoding at the receiver. Since wireless technologies become a very high demand nowadays, OSTBC has been chosen to be a subject study for different digital modulation schemes [5,7, 8]. |
| The present study involves a number of procedures namely simulations of the 2X2 MIMO transmission system, OSTBC multiplexing, Digital modulation and computation and comparison of BER for different SNR. The aim of the study is to identify appropriate modulation techniques and detector for MIMO system that gives better Bit Error Rate (BER) performance for different digital modulation Schemes (BPSK, QPSK, 16-QAM) using MATLAB simulation. |
LITERATURE SURVEY |
| In [1], The outline is variety of cost, technology and regulatory constraints make such a brute force solution unattractive if not impossible. The use of multiple antennas at transmitter and receiver, popularly known as multiple input multiple-output (MIMO) wireless is an emerging cost-effective technology that offers substantial leverages in making 1Gbps wireless links a reality. This paper provides an overview of MIMO wireless technology covering channel models, performance limits, coding and transceiver design. In [13], the diversity analysis of MIMO systems using STBC codes and OSTBC codes was studied and BER vs. Eb/N0 values were measured. In this paper both 2x2 & 8x2 MIMO systems are compared with space time and orthogonal space time block codes with ML and MRC detectors at the receiver. In [8], Data is encoded using a space–time block code and the encoded data is split into n streams which are simultaneously transmitted using n transmit antennas. The received signal at each receive antenna is a linear superposition of the n transmitted signals perturbed by noise. Maximum-likelihood decoding is achieved in a simple way through decoupling of the signals transmitted from different antennas rather than joint detection. This uses the orthogonal structure of the space–time block code and gives a maximum-likelihood decoding algorithm which is based only on linear processing at the receiver. Space–time block codes are designed to achieve the maximum diversity order for a given number of transmit and receive antennas subject to the constraint of having a simple decoding algorithm. The classical mathematical framework of orthogonal designs is applied to construct space–time block codes. It is shown that space–time block codes constructed in this way only exist for few sporadic values of n. Subsequently, a generalization of orthogonal designs is shown to provide space–time block codes for both real and complex constellations for any number of transmit antennas. For an arbitrary complex constellation such as PSK and QAM, space–time block codes are designed that achieve ½ of the maximum possible transmission rate for any number of transmit antennas. For the specific cases of two, three, and four transmit antennas, space–time block codes are designed that achieve, respectively, all, 3/4, and 3/4 of maximum possible transmission rate using arbitrary complex constellations. The best tradeoff between the decoding delay and the number of transmit antennas is also computed and it is shown that many of the codes presented here are optimal in this sense as well |
MULTIPLE INPUT MULTIPLE OUTPUT (MIMO) |
| Multiple-input multiple-output (MIMO) systems are known to offer a wide variety of benefits over conventional singleinput single-output (SISO) systems, such as the potential to facilitate significantly higher data rates or to considerably improve the reliability of a wireless link. A promising approach for exploiting the spatial diversity that becomes available if multiple antennas are used is to utilize orthogonal space- time block codes (OSTBC), for example, which are capable of extracting full diversity gain from a MIMO channel with only moderate encoding and decoding complexity [2]. |
 |
| In MIMO systems, a transmitter sends multiple streams by multiple transmit antennas. The transmit streams go through a matrix channel which consists of all NtNr paths between the Nt transmit antennas at the transmitter and Nr receive antennas at the receiver. Then, the receiver gets the received signal vectors by the multiple receive antennas and decodes the received signal vectors into the original information. A narrow band flat fading MIMO system is modeled as |
| Where y and x are the receive and transmit vectors, respectively and H and n are the channel matrix and the noise vector, respectively. Referring to information theory, the ergodic channel capacity of MIMO systems where both the transmitter and the receiver have perfect instantaneous channel state information is |
 |
| A MIMO detector which is used for detecting receive symbols, corresponds to symbols transmitted through transmit antennas from receive signals, when the transmit data transmitted by the terminal group are received through receive antennas. A terminal identifier is used for identifying the receive symbols detected by the MIMO detector as symbols which correspond to respective terminals in the terminal group. A symbol demapper for demapping the receive symbols is identified by the terminal identifier to convert binary data which correspond to a modulation method used by the terminal. Group and a reverse data processor are used for performing de-interleaving, decoding of error correction codes and descrambling on the binary data which is demapped by the symbol demapper and detecting receive data of the respective terminals. The symbol demapper and the reverse data processor are provided as the same number as that of the terminals in the terminal group. The terminal of the terminal group comprises: a data processor for performing scrambling, error correction encoding and interleaving on the transmit data and processing them as binary data. A symbol mapper for mapping the binary data transmitted by the data processor according to a desired modulation method; and a parallel converter for paralleling the symbols mapped by the symbol mapper to the respective antennas, and providing them by consideration of the number of the transmit antennas [13]. |
| A spatial multiplexing detection method using a MIMO technology comprises: |
| The purpose of solving the issues like what error rate can be tolerated, what is the ultimate measure of performance (e.g., frame-error-rate, worst-case complexity, or average complexity), and what computational platform is used. Additionally, the bits may be part of a larger code word and different vectors in that code word may either see the same H (slow fading) or many different realizations of H (fast fading). This complicates the picture, because notions that are important in slow fading (such as spatial diversity) are less important in fast fading, where diversity is provided anyway by time variations. |
| The multiple input multiple output code division multiple access systems can get good performance or high capacity, but the computational complexity of detection is usually high. When the SNR is high enough, it simply outputs the zero forcing detection results, which leads to a faster detecting process [4, 6]. |
ORTHOGONAL SPACE TIME BLOCK CODE (OSTBC) |
| Orthogonal STBCs are an important subclass of linear STBCs that guarantee that the ML detection of different symbols {sn} is decoupled and at the same time the transmission scheme achieves a diversity order equal to ntnr. The main disadvantage of OSTBCs is the facts that for more than two transmit antennas and complex-valued signals, OSTBCs only exist for code rates smaller than one symbol per time slot. |
| An OSTBC is a linear space-time block code S that has the following unitary property. |
| The ith row of S corresponds to the symbols transmitted from the ith transmit antenna in N transmission periods, while the jth column of S represents the symbols transmitted simultaneously through nt transmit antennas at time j. According to equation (5), the columns of the transmission matrix S are orthogonal to each other. That means that in each block, the signal sequences from any two transmit antennas are orthogonal. The orthogonality enables us to achieve full transmit diversity and at the same time, it allows the receiver by means of simple MRC to decouple the signals transmitted from different antennas and consequently, it allows a simple ML decoding [8]. |
RAYLEIGH CHANNEL |
| Rayleigh Channel Constructive and destructive nature of multipath components in flat fading channels can be approximated by Rayleigh distribution if there is no line of sight which means when there is no direct path between transmitter and receiver. The received signal can be simplified to: |
 |
MIMO RECEIVER DESIGN |
| A problem encountered in the design of receivers for digital communication systems is the detection of data from noisy measurements of the transmitted signals. In any realistic scenario the receiver is due to the noise bound to make occasional errors. Therefore, designing a receiver which has the property that this probability of error is minimal is appealing, both from a practical and a theoretical point of view. Unfortunately, such designs tend to result in computationally complex receivers and for this reason they are often abandoned in favour of computationally simpler but suboptimal receivers. It is well known that for many scenarios the gap in performance between suboptimal and the optimal receivers is substantial. This alone makes the optimal receivers interesting. Additionally, the decreasing cost of computation will result in computationally feasible optimal designs [7, 13]. |
| The fig.2 shows the probable MIMO transmission schemes with 2 transmit antennas and 2 receive antennas. |
 |
| In MIMO wireless communication, an equalizer is employed to recover the signal. The equalizer is a device that attempts to reverse the distortion incurred by a signal transmitted through a channel. Its purpose is to reduce inter symbol interference to allow recovery of the transmit symbols. |
DETECTION USING SUCCESSIVE INTERFERENCE CANCELLATION |
ZERO FORCING (ZF) EQUALIZER FOR 2×2 MIMO CHANNEL |
| The ZF receiver completely nulls out the influence of the interference signals coming from other transmit antennas and detects every data stream separately. The disadvantage of this receiver is that due to cancelling the influence of the signals from other transmit antennas, the additive noise may be strongly increased and thus the performance may degrade heavily. Due to the separate decision of every data stream, the complexity of this algorithm is much lower than in case of an ML receiver. An attempt is made to improve the bit error rate performance by trying out Successive Interference Cancellation (SIC). We will assume that the channel is a flat fading Rayleigh multipath channel and the modulation is BPSK. To do the SIC, the receiver needs to perform the following. |
| Using the ZF equalization approach described above, the receiver can obtain an estimate of the two transmitted symbols x1, x2 , i.e., we discuss the case where there a multiple transmit antennas and multiple receive antennas resulting in the formation of a Multiple Input Multiple Output (MIMO) channel. In this section, we will restrict our discussion to a 2 transmit 2 receive antenna case (resulting in a 2×2 MIMO channel). We will assume that the channel is a flat fading Rayleigh multipath channel and that different modulation schemes are used [17]. |
| Let us now try to understand the process for extracting the two symbols which interfered with each other. In the first time slot, the received signal on the first receive antenna is, |
 |
| We assume that the receiver knows h1,1, h1,2, h2,1 and h2,2. The receiver also knows y1 and y2. The unknowns are x1 and x2. The two equations with two unknowns can be solved. For convenience, the above equation can be represented in matrix notation, equivalently, |
 |
MINIMUM MEAN SQUARE ERROR (MMSE) EQUALIZER FOR 2×2 MIMO CHANNEL |
| The MMSE receiver compromises between noise enhancement and signal interference and minimizes the mean squared error between the transmitted symbol and the detected symbol. Thus the results of the MMSE equalization are the transmitted data streams plus some residual interference and noise. After MMSE equalization each data stream is separately detected (quantized) in the same way as in the ZF case. In practice it can be difficult to obtain correct parameter values of the noise that is necessary for optimum signal detection and only a small improvement compared to the ZF receiver can be obtained. Therefore, this receiver is not used in practice. |
| The MMSE approach tries to find a coefficient W which minimizes the criterion, |
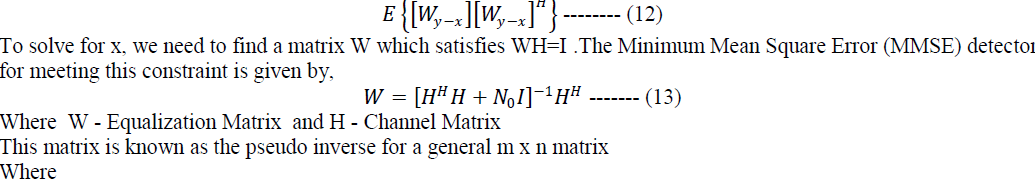 |
 |
| In fact, when the noise term is zero, the MMSE equalizer reduces to Zero Forcing equalizer. This model can be extended to m x n antenna configuration [6, 14]. |
MAXIMUM LIKELIHOOD (ML) DETECTOR FOR 2×2 MIMO CHANNEL |
| Maximum Likelihood (ML) Receiver achieves the best system performance (maximum diversity and lowest bit error ratio (BER) can be obtained), but needs the most complex detection algorithm. The ML receiver calculates all possible noiseless receive signals by transforming all possible transmit signals by the known MIMO channel transfer matrix. Then it searches for that signal calculated in advance, which minimizes the Euclidean distance to the actually received signal. The undisturbed transmit signal that leads to this minimum distance is considered as the most likely transmit signal. Note that the above described detection process is optimum in sense of BER for white Gaussian noise. |
| The Maximum Likelihood receiver tries to find ïÿýïÿý which minimizes, J = y − Hx 2 . |
 |
RESULTS AND DISCUSSIONS |
| The simulation results of the performance of OSTBC for different digital modulation techniques BPSK, QPSK, and 16- QAM for Rayleigh channel with different detectors are derived using MATLAB simulation. The BER values as a function of SNR are determined by combining the successive interference cancellation techniques with ZF, MMSE and ML detector systems and modulation schemes for studying their relative performances in digital modulation. The SNR values are determined as a function of BER for each BPSK, QPSK and 16-QAM modulation schemes. The bit-errorrate performances derived as a function of SNR for 2X2 MIMO-OSTBC multiplexing system for the three detector systems are shown in Fig. 3 for BPSK modulation, Fig. 4 for QPSK modulation and Fig. 5 for 16 QAM modulation. |
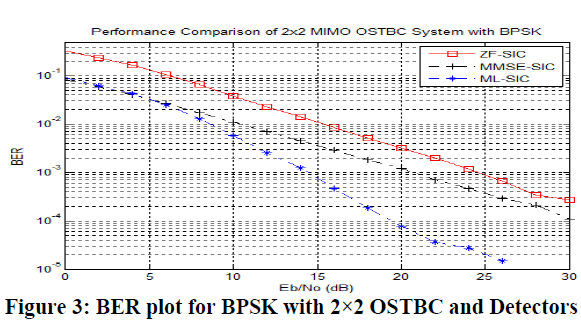 |
| It is seen from Fig. 3 that the BER values decreases as SNR increases for all the three types of detectors. The figure indicates that at BER ~10-3, the ZF detector shows that the SNR ~24.46 dB, MMSE detector SNR ~20.6 dB and ML detection SNR ~14.46 dB can be achievable for the BPSK modulation. The result clearly demonstrates that the SNR values are found to be lower ~10 dB for ML detectors compared to other detector systems suggesting that ML detectors are more efficient for MIMO-OSTBC transmission systems. |
 |
| It can be seen from Fig. 4 that the BER values decreases as SNR increases for all the three types of detectors. The figure indicates that at BER ~10-3, for the ZF detectors SNR ~26.12dB with MMSE detectors the SNR ~21.15dB and ML detectors the SNR ~14.8dB achievable for the QPSK modulation. The results clearly demonstrate that the SNR values are the lower ~11.32dB for ML detectors compared to other detector systems suggesting that ML detectors are more efficient for MIMO-OSTBC transmission systems. |
 |
| It can be seen from Fig. 5 that the BER values decreases as SNR increases for all the three types of detectors. The figure indicates that at BER ~10-3, for the ZF detectors SNR ~26.48dB, MMSE detectors SNR ~22.05dB and ML detectors SNR ~15.15dB achievable for the 16-QAM modulation. The results clearly demonstrate that for 16 QAM modulation the SNR values are the lower ~11.33dB for ML detectors compared to other detector systems suggesting that ML detectors are more efficient for MIMO-OSTBC transmission systems. |
| The simulation results at BER ~10-3, the SNR performance of 2X2 MIMO-OSTBC obtained for three types of detectors techniques ZF, MMSE and ML for different modulation schemes BPSK, QPSK and 16-QAM are summarized in Table 1. |
 |
| Table-1- Comparison of ZF-SIC, MMSE-SIC and ML-SIC detectors, SNR Values for different modulation techniques for BER ~10-3 |
| It is also evident from the Table 1 that at BER ~10-3, all the three detectors depicts as expected similar behavior and the SNR values increases as we go higher from BPSK to 16-QAM modulation scheme. Further it is clearly demonstrated that the SNR values for the ML detectors at BER ~10-3 shows lowest values for all the three modulation schemes and displays much better SNR performance >10 dB compared to other detection systems. |
CONCLUSIONS |
| It can be concluded from the results presented that, |
| 1. For a 2x2 MIMO system, with OSTBC modulation at BER 10-3, the SNR values increases only by ~4dB with increasing modulation from BPSK to 16-QAM |
| 2. For the same MIMO multiplexing system at BER 10-3, the ML detection shows lowest values of SNR ~14.46 dB compared to ZF and MMSE detection system. |
| 3. The SNR performance of ML detectors at BER values ~10-3 indicates improvement >10 dB for the ML detectors compared to ZF and MMSE detection systems. |
| 4. It can be concluded from the simulation studies that the MIMO-OSTBC transmission system offers better SNR performances for BPSK modulation with ML-SIC detection system. |
References |
|